研究动机: 神经网络彻底改变了机器智能的许多领域,实现了超人的准确性。然而,提高准确性的驱动力往往需要付出代价:现代先进网络需要高度计算资源,超出许多移动和嵌入式应用的能力。
主要贡献: 发明了一个新的层模块, 具有线性瓶颈的倒置残差(inverted residual)。
相关工作: 里面介绍了近来整个领域的发展概况, 看论文就看介绍的吧.
基本概念
深度可分离卷积
Depthwise Separable Convolutions = depthwise + pointwise
如果卷积核大小为 3x3, 深度可分离卷积的计算量为常规卷积的 (1/9, 1/8)
流形(manifold)
花书 <<深度学习>> 介绍:
(color{red}{流形(manifold)}) 指连接在一起的区域。数学上,它是指一组点,且每个点都 有其邻域。给定一个任意的点,其流形局部看起来像是欧几里得空间。日常生活中, 我们将地球视为二维平面,但实际上它是三维空间中的球状流形。
每个点周围邻域的定义暗示着存在变换能够从一个位置移动到其邻域位置。例 如在地球表面这个流形中,我们可以朝东南西北走。
尽管术语 “流形’’ 有正式的数学定义, 但是机器学习倾向于更松散地定义一组 点,只需要考虑少数嵌入在高维空间中的自由度或维数就能很好地近似。每一维都对应着局部的变化方向。如图 5.11 所示, 训练数据位于二维空间中的一维流形中。 在机器学习中,我们允许流形的维数从一个点到另一个点有所变化。这经常发生于流形和自身相交的情况中。例如,数字 "8" 形状的流形在大多数位置只有一维,但 在中心的相交处有两维。
(color{red}{流形学习(manifoldspace learning)}) 算法假设: 该假设认为 (R^n) 中大部分区域都是无效的输入,有意义的输入只分布在包 含少量数据点的子集构成的一组流形中,而学习函数的输出中,有意义的变化都沿着流形的方向或仅发生在我们切换到另一流形时。
数据位于低维流形的假设并不总是对的或者有用的。我们认为在人工智能的一 些场景中,如涉及到处理图像、声音或者文本时,流形假设至少是近似对的。
Linear Bottlenecks
Linear Bottlenecks 理论支持:
考虑由 n 层 (L_i) 组成的深层神经网络,其中每一层都具有尺寸为 (h_i×w_i×d_i)的激活张量。在本节中,我们将讨论这些激活张量的基本属性,我们将其视为具有 (d_i) 维度的 (h_i×w_i)“像素”的容器。非正式地说,对于输入的一组真实图像,我们说层激活(对于任何层 (L_i))形成一个“流形”。由于这种流形通常不能用分析方法描述,因此我们将凭经验研究它们的性质。例如,长期以来一直认为神经网络中感兴趣的流形可以嵌入到低维子空间中。换句话说,当我们查看深卷积层的所有单个通道像素时,这些值中编码的信息实际上位于某个流形中,而这又可嵌入到低维子空间中。
乍一看,这样的事实可以通过简单地减少层的维度来捕获和利用,从而降低操作空间的维度。这已经被 MobileNetV1 成功利用,通过宽度乘法器参数在计算和精度之间进行有效的折中. 遵循这种直觉,宽度乘法器方法允许减小激活空间的维度,直到感兴趣的流形横跨整个空间为止。然而,当我们回想到深度卷积神经网络实际上具有非线性的坐标变换(例如ReLU)时,这种直觉就会崩溃。例如,ReLU应用于1D空间中的线会产生'射线',在 (R^n) 空间中,其通常导致具有 n 截的分段线性曲线。
insight:
- 如果流形在ReLU变换后保持非零卷 (no-zero volume),则它对应于线性变换.
- ReLU能够保留关于输入流形的完整信息,但只有当输入流形位于输入空间的低维子空间时。
这两个见解为我们提供了一个优化现有神经架构的经验提示:假设感兴趣的流形是低维的,我们可以通过将线性瓶颈层插入卷积模块来捕获这一点。 实验证据表明,使用线性层非常重要,因为它可以防止非线性破坏太多的信息。
Inverted residuals
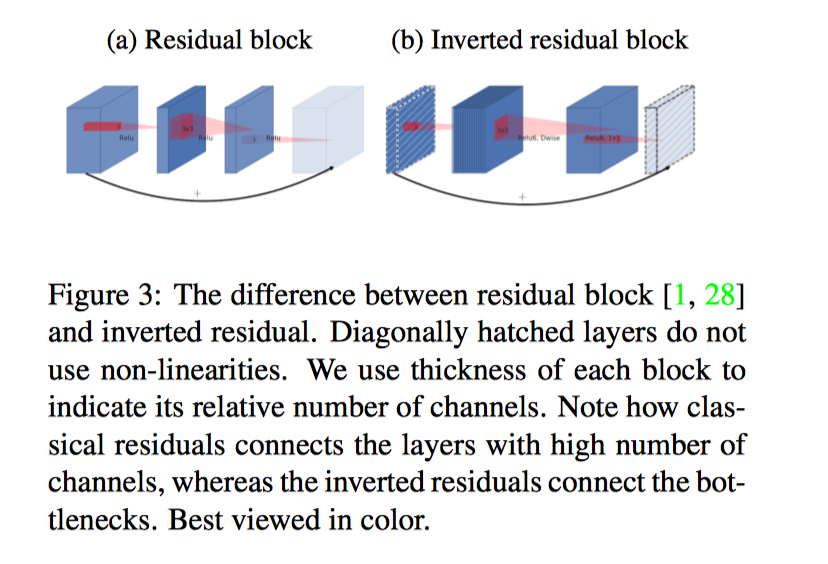 

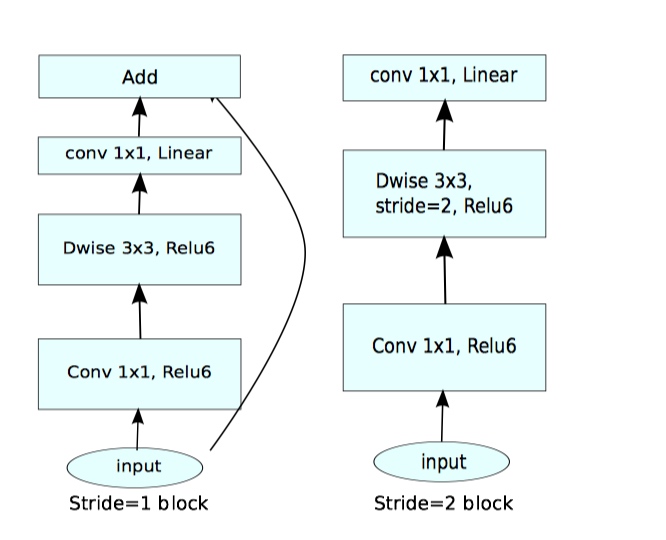
We will refer to the ratio between the size of the input bottleneck and the inner size as the expansion ratio.
(color{red}{由于 Inverted space residuals 两边 thin, 所以该设计想比较传统残差设计更加节省内存})
论文观点
架构的一个有趣特性是它在构建块(瓶颈层)的输入/输出域与层转换(这是一种将输入转换为输出的非线性函数)之间提供了自然分离. 前者(层输入/输出)可以看作是网络在每一层的容量,而后者(层转换)则是表达力。这与常规和可分离的传统卷积块相反,其中表现力和容量都缠结在一起,并且是输出层深度的函数。
(color{red}{在论文的最后提出}):
On the theoretical side: the proposed convolutional block has a unique property that allows to separate the network expressivity (encoded by expansion layers) from its capacity (encoded by bottleneck inputs). Exploring this is an important direction for future research.
这种解释使我们能够独立于其容量研究网络的表现力,并且我们认为需要进一步探索这种分离,以便更好地理解网络性质.
我的理解:
- 由于文中在前面提到, 当流型存在于高维输入空间的低纬空间时, 通过 Relu 几乎可以保留全部信息
- 在 bottleneck inputs 之后的 expansion layers 会有 1x1 卷积升维操作, 所以认为经过 Relu 没有损失信息, 即模型的容量不变, expansion layers的操作可以看做是层的表达力, 然后通过 Linear Bottlenecks, 也没有损失信息, 故全程保持模型的容量不变, 可以通过调节 expansion ratio, t 来调节模型的表达力
网络结构
实现细节:
base learning rate = 0.045
weight decay = 0.00004
t = 5 - 10
dropout + bn + relu6
RMSPropOptimizer momentum = 0.9 decay = 0.9
网络结构

 

表中错误已修正
内存节约型 inference
计算图 G, 在推导时(inference ), 内存总量和边界如下:
内存占用量是所有操作对应输入和输出张量的总大小与操作本身所占内存之和决定。 如果我们将瓶颈残差块视为单一操作(并将内部卷积视为一次性张量[即用完就丟]),则总内存量将由瓶颈张量的大小决定,而不是瓶颈内部张量的大小决定