Numpy 多维数组简介



NumPy是一个功能强大的Python库，主要用于对多维数组执行计算。NumPy这个词来源于两个单词-- Numerical和Python。NumPy提供了大量的库函数和操作，可以帮助程序员轻松地进行数值计算。

NumPy中的ndarray是一个多维数组对象，该对象由两部分组成：

1. 实际的数据；
2. 描述这些数据的元数据。

大部分的数组操作仅仅修改元数据部分，而不改变底层的实际数据。

1.创建数组

NumPy 中的数组
创建Numpy数组的不同方式

In [29]: np.array([i for i in np.arange(1, 10, 2)])
Out[29]: array([1, 3, 5, 7, 9])

n [30]: np.ones(5)
Out[30]: array([ 1.,  1.,  1.,  1.,  1.])

In [33]: np.zeros((2, 3))
Out[33]:
array([[ 0.,  0.,  0.],
       [ 0.,  0.,  0.]])
       
In [13]: np.random.random((2, 3))
Out[13]:
array([[ 0.14455294,  0.42025496,  0.4699947 ],
       [ 0.87092512,  0.41076888,  0.63422374]])

In [17]: np.linspace(0, 2*np.pi, 5)
Out[17]: array([ 0.        ,  1.57079633,  3.14159265,  4.71238898,  6.28318531])

NumPy提供了一种提取多维数组的行/列的强大方法。

In [14]: arr =  np.random.random((2, 3))

In [15]: arr
Out[15]:
array([[ 0.19390068,  0.50111214,  0.75457138],
       [ 0.60723086,  0.87995546,  0.7037096 ]])

In [16]: arr[:, 2]
Out[16]: array([ 0.75457138,  0.7037096 ])

In [17]:

Numpy 的逐元素向量操作示例

import numpy as np 
a = np.array([[1.0, 2.0], [3.0, 4.0]]) 
b = np.array([[5.0, 6.0], [7.0, 8.0]]) 
sum = a + b 
difference = a - b 
product = a * b 
quotient = a / b 
print("Sum = 
", sum)
print("Difference = 
", difference) 
print("Product = 
", product) 
print("Quotient = 
", quotient) 

# The output will be as follows: 

Sum = [[ 6. 8.] [10. 12.]]
Difference = [[-4. -4.] [-4. -4.]]
Product = [[ 5. 12.] [21. 32.]]
Quotient = [[0.2 0.33333333] [0.42857143 0.5 ]]

运算法 * 是矩阵逐元素乘法, 矩阵乘法如下

matrix_product = a.dot(b) 
print "Matrix Product = ", matrix_product

# 输出
[[19. 22.]
[43. 50.]]

2.矩阵

NumPy简单入门教程

In [22]: a = np.array([[11, 12, 13, 14, 15],
    ...:               [16, 17, 18, 19, 20],
    ...:               [21, 22, 23, 24, 25],
    ...:               [26, 27, 28 ,29, 30],
    ...:               [31, 32, 33, 34, 35]])
    ...:
    ...:

In [23]: a[2][4]
Out[23]: 25

In [24]: a[2, 4]
Out[24]: 25

索引切片

# MD slicing
print(a[0, 1:4])  # >>>[12 13 14]
print(a[1:4, 0])  # >>>[16 21 26]
print(a[::2,::2]) # >>>[[11 13 15]
                  #     [21 23 25]
                  #     [31 33 35]]
print(a[:, 1])    # >>>[12 17 22 27 32]

如你所见，通过对每个以逗号分隔的维度执行单独的切片，你可以对多维数组进行切片。因此，对于2D数组，我们的第一片定义了行的切片，第二片定义了列的切片。

高阶索引

索引进阶

花式索引

花式索引(Fancy indexing)是获取数组中我们想要的特定元素的有效方法。

# 向量
a = np.arange(0, 100, 10)
indices = [1, 5, -1]
b = a[indices]
print(a) # >>>[ 0 10 20 30 40 50 60 70 80 90]
print(b) # >>>[10 50 90]

# 矩阵
In [33]: a
Out[33]:
array([[11, 12, 13, 14, 15],
       [16, 17, 18, 19, 20],
       [21, 22, 23, 24, 25],
       [26, 27, 28, 29, 30],
       [31, 32, 33, 34, 35]])

In [34]: idx = [[2, 3, 1], [4, 4, 2]]

In [35]: a[idx]
Out[35]: array([25, 30, 18])

正如你在上面的示例中所看到的，我们使用我们想要检索的特定索引序列对数组进行索引。这反过来返回我们索引的元素的列表。

布尔屏蔽
布尔屏蔽是一个有用的功能，它允许我们根据我们指定的条件检索数组中的元素。

Boolean masking

import matplotlib.pyplot as plt

a = np.linspace(0, 2 * np.pi, 50)
b = np.sin(a)
plt.plot(a,b)
mask = b >= 0
plt.plot(a[mask], b[mask], 'bo')
mask = (b >= 0) & (a <= np.pi / 2)
plt.plot(a[mask], b[mask], 'go')
plt.show()

上面的示例显示了如何进行布尔屏蔽。你所要做的就是将数组传递给涉及数组的条件，它将为你提供一个值的数组，为该条件返回true。

该示例生成以下图：



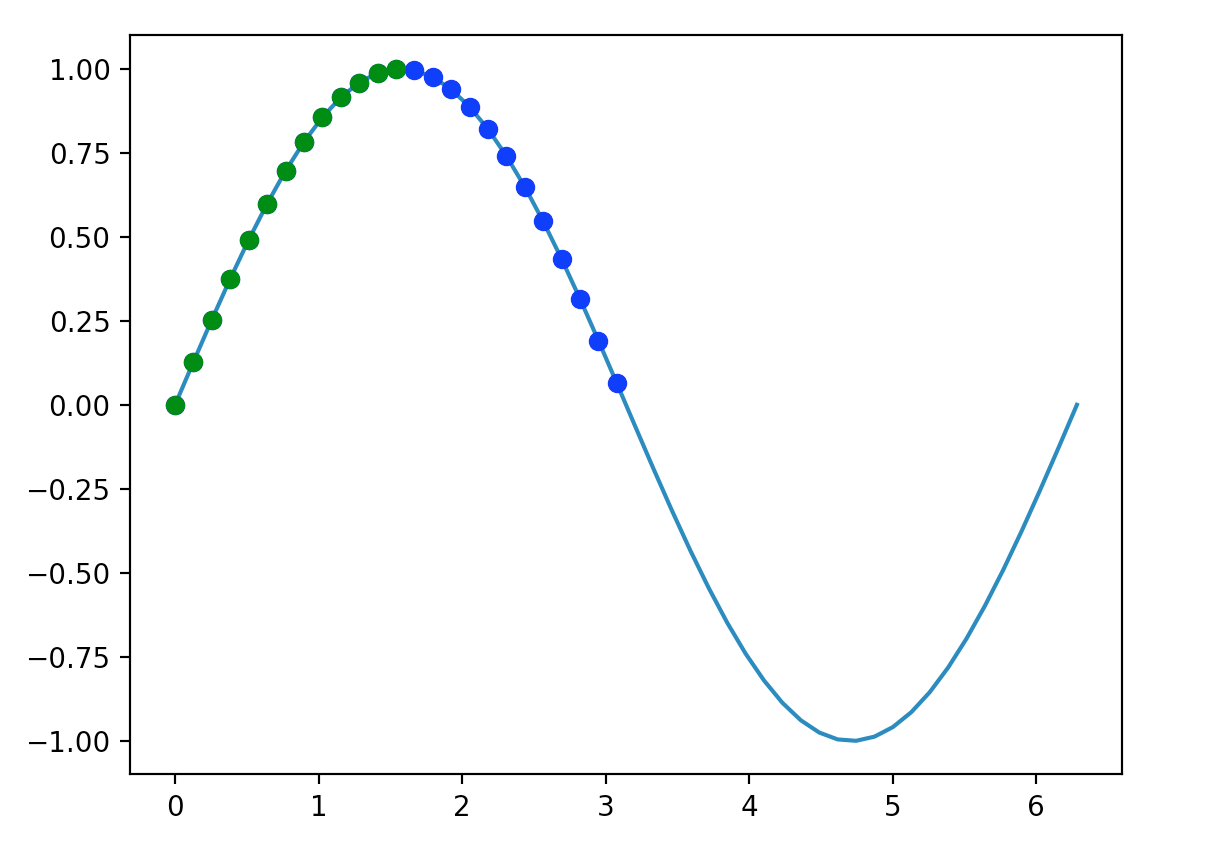
我们利用这些条件来选择图上的不同点。蓝色点(在图中还包括绿点，但绿点掩盖了蓝色点)，显示值大于0的所有点。绿色点表示值大于0且小于一半π的所有点。

缺省索引

不完全索引是从多维数组的第一个维度获取索引或切片的一种方便方法。

例如，如果数组a=[1，2，3，4，5]，[6，7，8，9，10]，那么[3]将在数组的第一个维度中给出索引为3的元素，这里是值4。

# Incomplete Indexing
In [40]: a = np.arange(0, 100, 10)
In [41]: a
Out[41]: array([ 0, 10, 20, 30, 40, 50, 60, 70, 80, 90])

In [42]: a[:5]
Out[42]: array([ 0, 10, 20, 30, 40])

In [43]: a[a >= 50]
Out[43]: array([50, 60, 70, 80, 90])

In [44]: a[::2]
Out[44]: array([ 0, 20, 40, 60, 80])

where函数

where() 函数是另外一个根据条件返回数组中的值的有效方法。只需要把条件传递给它，它就会返回一个使得条件为真的元素的列表。

a = np.arange(0, 100, 10)
b = np.where(a < 50) 
c = np.where(a >= 50)[0]
print(b) # >>>(array([0, 1, 2, 3, 4]),)
print(c) # >>>[5 6 7 8 9]


np.where([[True, False], [True, True]],
         [[1, 2], [3, 4]],
         [[9, 8], [7, 6]])
# output
array([[1, 8],
       [3, 4]])

3.数组属性

在使用 NumPy 时，你会想知道数组的某些信息。很幸运，在这个包里边包含了很多便捷的方法，可以给你想要的信息。

# Array properties
a = np.array([[11, 12, 13, 14, 15],
              [16, 17, 18, 19, 20],
              [21, 22, 23, 24, 25],
              [26, 27, 28 ,29, 30],
              [31, 32, 33, 34, 35]])

print(type(a))    # >>><class 'numpy.ndarray'>
print(a.dtype)    # >>>int64
print(a.size)     # >>>25
print(a.shape)    # >>>(5, 5)
print(a.itemsize) # >>>8
print(a.ndim)     # >>>2
print(a.nbytes)   # >>>200

数组的形状是它有多少行和列，上面的数组有5行和5列，所以它的形状是(5，5)。

• itemsize属性是每个项占用的字节数。这个数组的数据类型是int 64，一个int 64中有64位，一个字节中有8位，除以64除以8，你就可以得到它占用了多少字节，在本例中是8。

• ndim 属性是数组的维数。这个有2个。例如，向量只有1。

• nbytes 属性是数组中的所有数据消耗掉的字节数。你应该注意到，这并不计算数组的开销，因此数组占用的实际空间将稍微大一点。

4.常见操作

操作	解释
max	某个维度最大值
min	某个维度最小值
mean	某个维度均值
cursum	累积和
reshape