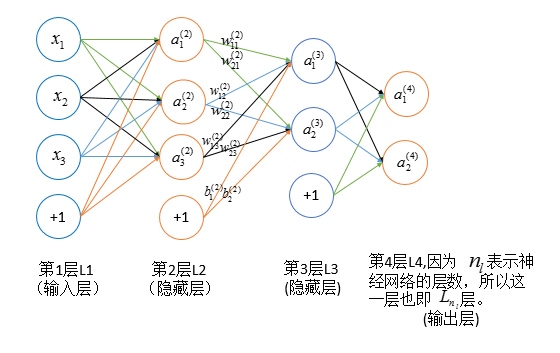 

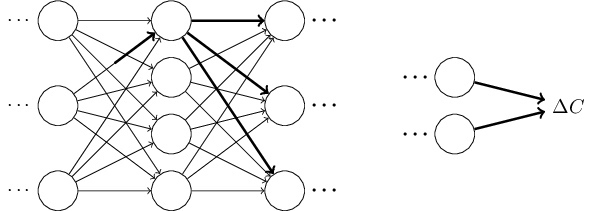
神经网络中权重 (w^{(l)}_{ij}) 的改变将影响到接下来的网络层,直到输出层,最终影响损失函数

(color{red}{公式推导符号说明})
| 符号 | 说明 |
|---|---|
| (n_l) | 网络层数 |
| (y_j) | 输出层第 (j) 类 标签 |
| (S_l) | 第 (l) 层神经元个数(不包括偏置) |
| (g(x)) | 激活函数 |
| (w^{(l)}_{ij}) | 第 (l) 层第 (j) 个单元与第 (l+1) 层第 (i) 个单元之间的连接参数 |
| (b^{(l)}_i) | 第 (l+1) 层第 (i) 个单元的偏置 |
| (z^{(l)}_i) | 第 (l) 层第 (i) 个单元的输入加权和(包含偏置) |
| (a^{(l)}_i) | 第 (l) 层第 (i) 个单元的激活值(输出值) |
| (delta^{(l)}_i) | 第 (l) 层第 (i) 个单元的梯度值 |
MSE 损失函数推导
(color{red}{基本公式})
[egin{align*}
z^{(l+1)}_i &= b^{(l)}_i + sum^{S_l}_{j=1}{w^{(l)}_{ij}a^{(l)}_j} ag{1} \
g(x) &= frac{1}{1 + e^{-x}} ag{2}\
a^{(l)}_i &= g(z^{(l)}_i) ag{3} \
J( heta) &= frac12{{sum^{S_{n_l}}_{j=1}ig ({y_j - a^{(n_l)}_j}}}ig)^2 ag{4}\
delta^{(l)}_i &=frac{partial{J( heta)}}{partial{z^{(l)}_i}} ag{5} \
\
end{align*}
]
梯度反向传播公式推导
(color{red}{初始条件})
[egin{align*}
delta ^{ (n_{ l }) }_{ i }&=frac { partial { J( heta ) } }{ partial { z^{ (n_{ l }) }_{ i } } } \ &=frac { 1 }{ 2 } frac { partial { } }{ partial { z^{ (n_{ l }) }_{ i } } } sum _{ j=1 }^{ S_{ n_l } } left( y_{ j }-a^{ (n_{ l }) }_{ j }
ight) ^{ 2 }\
&=frac { 1 }{ 2 } frac { partial { } }{ partial { z^{ (n_{ l }) }_{ i } } } sum _{ j=1 }^{ S_{ n_l } } left( y_{ j }-g(z^{ (n_{ l }) }_{ j })
ight) ^{ 2 }\
&=frac { 1 }{ 2 } frac { partial { } }{ partial { z^{ (n_{ l }) }_{ i } } } left( y_{ i }-g(z^{ (n_{ l }) }_{ i })
ight) ^{ 2 }\
&=-left( y_{ i }-a^{ (n_{ l }) }_{ i }
ight) gprime (z^{ (n_{ l }) }_{ i })\
end{align*}
]
(color{red}{递推公式})
[egin{align*}
delta ^{ (l) }_{ i }&=frac { partial { J( heta ) } }{ partial { z^{ (l) }_{ i } } } \
&=sum _{ j=1 }^{ S_{ l+1 } } frac { partial { J( heta ) } }{ partial { z^{ (l+1) }_{ j } } } frac { partial { z^{ (l+1) }_{ j } } }{ partial { a^{ (l) }_{ i } } } frac { partial { a^{ (l) }_{ i } } }{ partial { z^{ (l) }_{ i } } } \
&=sum_{ j=1 }^{ S_{ l+1 } } frac { partial { J( heta ) } }{ partial { z^{ (l+1) }_{ j } } } frac { partial { } }{ partial { a^{ (l) }_{ i } } } left( b^{ (l) }_{ j }+sum _{ k=1 }^{ S_{ l } } w^{ (l) }_{ jk }a^{ (l) }_{ k })
ight) frac { partial { a^{ (l) }_{ i } } }{ partial { z^{ (l) }_{ i } }} \
&=sum_{ j=1 }^{ S_{ l+1 } } delta ^{ (l) }_{ j } w^{ (l) }_{ ji }gprime (z^{ (l) }_{ i }) \
&= gprime (z^{ (l) }_{ i }) sum_{ j=1 }^{ S_{ l+1 } } delta ^{ (l+1) }_{ j } w^{ (l) }_{ ji } \
end{align*}
]
(color{red}{损失函数关于权重和偏置的导数})
[egin{align*}
\
frac { partial { J( heta ) } }{ partial { w^{ (l) }_{ ij } } } &=frac { partial { J( heta ) } }{ partial { z^{ (l+1) }_{ i } } } frac { partial { z^{ (l+1) }_{ i } } }{ partial { w^{ (l) }_{ ij } } } \
&=delta ^{ (l+1) }_{ i }frac { partial { z^{ (l+1) }_{ j } } }{ partial { w^{ (l) }_{ ij } } } \
&=delta ^{ (l+1) }_{ i }frac { partial { } }{ partial { w^{ (l) }_{ ij } } } left( b^{ (l) }_{ i }+sum _{ k=1 }^{ S_{ l } } w^{ (l) }_{ ik }a^{ (l) }_{ k })
ight) \ &=delta ^{ (l+1) }_{ i }a^{ (l) }_{ j }\
frac { partial { J( heta ) } }{ partial { b^{ (l) }_{ i } } } &=delta ^{ (l+1) }_{ i }
end{align*}
]
交叉熵损失函数推导
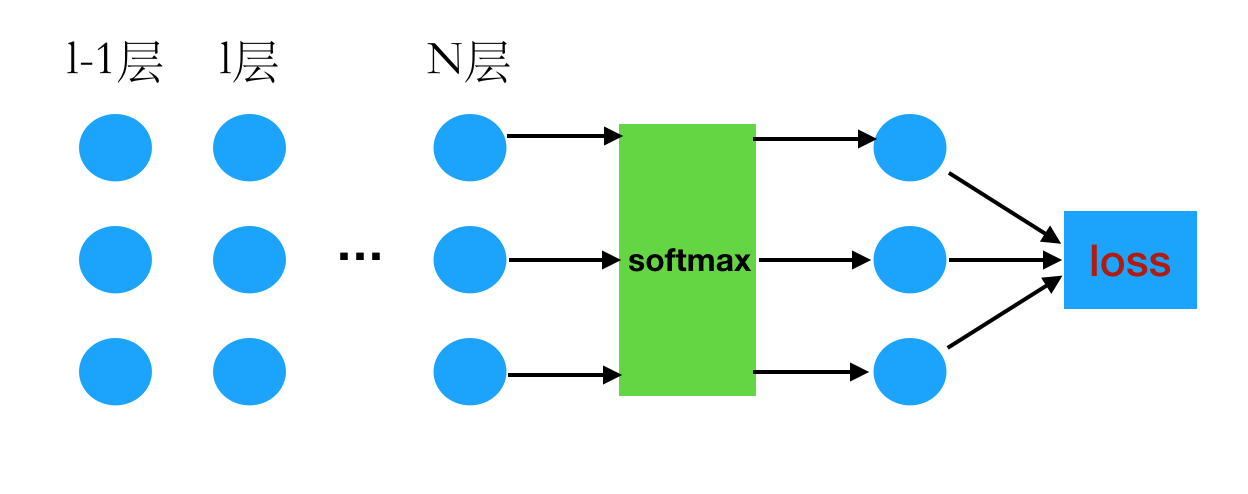 

(color{red}{递推公式})
[egin{align*}
g(x) &= frac{1}{1 + e^{-x}}quad quad 激活函数 \
a^{(l)}_{i} &= gleft(z^{(l)}_{i}
ight) \
z^{(l)}_{i} &= left( sum^{S_l}_{j=1}{w^{(l-1)}_{ij}a^{(l-1)}_i}
ight ) + b^{(l-1)}_i \
frac { partial { J( heta ) } }{ partial { z^{ (l) }_{ i } } }
&=sum _{ j=1 }^{ S_{ l+1 } } frac { partial { J( heta ) } }{ partial { z^{ (l+1) }_{ j } } } frac { partial { z^{ (l+1) }_{ j } } }{ partial { a^{ (l) }_{ i } } } frac { partial { a^{ (l) }_{i} } }{ partial { z^{ (l) }_{ i } } }\
end{align*}
]
其中
[egin{align*}
frac { partial { z^{ (l+1) }_{ j } } }{ partial { a^{ (l) }_{ i } } } &= w^{(l)}_{kj} \
frac { partial { a^{ (l) }_{i} } }{ partial { z^{ (l) }_{ i } } } &= z^{ (l) }_{ i } left(1- z^{ (l) }_{ i }
ight)
end{align*}
]
初始条件
[egin{align*}
J left( heta
ight ) &= -sum^{s_l}_{i=1}y^t space ln space y^p \
y^p_j &= frac{e^{a^N_j}}{sum^{s_N}_{k=1}e^{a^L_k}} \
end{align*}
]
[egin{align*}
J left( heta
ight ) &= -sum^{s_l}_{i=1}y^t space ln space y^p \
y^p_j &= frac{e^{a^N_j}}{sum^{s_N}_{k=1}e^{a^L_k}} \
end{align*}
]
softmax偏导数计算
[egin{align*}
frac{partial y^p_j}{partial a^N_i} =
egin{cases}
-y^p_i space y^p_j quad quad quadquad i
e j\
y^p_i space (1-y^p_i) quad quad space i =j
end{cases}
end{align*}
]
求导链式法则如下
[egin{align*}
frac { partial { J( heta ) } }{ partial { z^{ (N) }_{ i } } }
&= frac { partial { J( heta ) } }{ partial { a^{ (N) }_{ i } } } frac { { partial { a^{ (N) }_{ i } } } }{ partial { z^{ (N) }_{ i } } }
\
frac { partial { J( heta ) } }{ partial { a^{ (N) }_{ i } } }
&=sum _{ j=1 }^{ S_{ N } } frac { partial { J( heta ) } }{ partial { y^{ (p) }_{ j } } } frac { { partial { y^{ (p) }_{ j } } } }{ partial { a^{ (N) }_{ i } } } \
frac { partial { J( heta ) } }{ partial { y^{ (p) }_{ j } } } &= -frac{y^t_j}{y^p_j}
end{align*}
]
由上可知:
[egin{align*}
frac { partial { J( heta ) } }{ partial { a^{ (N) }_{ i } } }
&= frac { partial { J( heta ) } }{ partial { y^{ (p) }_{ i } } } frac { { partial { y^{ (p) }_{ i } } } }{ partial { a^{ (N) }_{ i } } } + sum _{ j
e i }^{ S_{ N } } frac { partial { J( heta ) } }{ partial { y^{ (p) }_{ j } } } frac { { partial { y^{ (p) }_{ j } } } }{ partial { a^{ (N) }_{ i } } }
\
&= - frac { y_{ i }^{ t } }{ y_{ i }^{ p } } y_{ i }^{ p }left( 1-y_{ i }^{ p }
ight) +sum _{ j
e i }^{ s_{ N } } -frac { y_{ j }^{ t } }{ y_{ j }^{ p } } left(- y_{ j }^{ p }y_{ i }^{ p }
ight) \
&= -y_{ i }^{ t }left( 1-y_{ i }^{ p }
ight) +sum _{ j
e i }^{ s_{ N } } left( y_{ j }^{ t }y_{ i }^{ p }
ight) \
&= -y^t_i + sum _{ j }^{ s_{ N } } left( y_{ j }^{ t }y_{ i }^{ p }
ight) \
&=y^p_i - y^t_i
end{align*}
]
由此可知反向传播迭代算法的初始值
[egin{align*}
frac { partial { J( heta ) } }{ partial { z^{ (N) }_{ i } } }
&= frac { partial { J( heta ) } }{ partial { a^{ (N) }_{ i } } } frac { { partial { a^{ (N) }_{ i } } } }{ partial { z^{ (N) }_{ i } } }
\
&=left( y^p_i - y^t_i
ight) cdot z^{ (l) }_{ i } left(1- z^{ (l) }_{ i }
ight) \
end{align*}
]