UVA1374-Power Calculus(迭代加深搜索)

Problem UVA1374-Power Calculus

Accept：107  Submit：584

Time Limit: 3000 mSec

 Problem Description

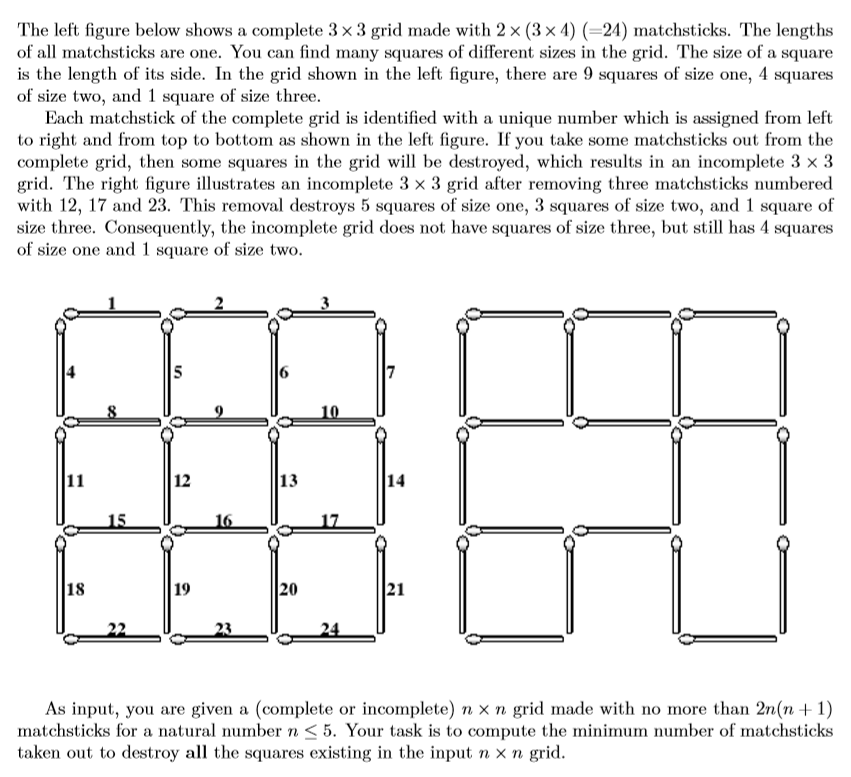
 Input

The input consists of several test cases. The number of test cases (T) is given in the first line of the input file. Each test case consists of two lines: The first line contains a natural number n, not greater than 5, which implies you are given a (complete or incomplete) n×n grid as input, and the second line begins with a nonnegative integer k, the number of matchsticks that are missing from the complete n×n grid, followed by k numbers specifying the matchsticks. Note that if k is equal to zero, then the input grid is a complete n×n grid; otherwise, the input grid is an incomplete n×n grid such that the specified k matchsticks are missing from the complete n×n grid.

 Output

Print exactly one line for each test case. The line should contain the minimum number of matchsticks that have to be taken out to destroy all the squares in the input grid.

 Sample Input

2 

2

0

3

3 12 17 23

 

 Sample Ouput

3

3

题解：IDA*算法，算法框架很简单，但是这个题的实现看上去就很困难，不超过60根火柴，因此用long long的二进制位来储存状态是很明智的，速度也比较快。

预处理出所有正方形的状态，存到数组里，对于搜索到的每一个状态，拿这些正方形去比对，如果有完整的正方形，就说明还没到最终状态判断是否能剪枝后return false或者继续递归。

剪枝挺粗暴的，如果有完整正方形，就把它的四个边全部去掉，但是h++，比对完之后，如果d+h还是大于maxd，那就必定要剪枝。

#include <iostream>
#include <cstring>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>

using namespace std;
typedef long long LL;

const int maxn = 65;
const int maxl = 10;

LL sqr[maxn];
LL one_sqr[maxl][maxl];

int n,edge_cnt,sqr_cnt;
int maxd;

int get_hor(int r,int c){
    return (2*n+1)*r+c+1;
}

int get_ver(int r,int c){
    return (2*n+1)*r+c+n+1;
}

inline LL get_LL(int p){
    return (LL)1 << (p-1);
}

void init(){
    scanf("%d",&n);
    edge_cnt = 2*n*(n+1);
    sqr_cnt = 0;
    for(int i = 0;i < n;i++){
        for(int j = 0;j < n;j++){
            one_sqr[i][j] = get_LL(get_hor(i,j)) | get_LL(get_hor(i+1,j)) | get_LL(get_ver(i,j)) | get_LL(get_ver(i,j+1));
            sqr[sqr_cnt++] = one_sqr[i][j];
        }
    }

    for(int size = 2;size <= n;size++){
        for(int i = 0;i+size <= n;i++){
            for(int j = 0;j+size <= n;j++){
                sqr[sqr_cnt] = 0;
                for(int k = 0;k < size;k++)
                    for(int l = 0;l < size;l++)
                        sqr[sqr_cnt] ^= one_sqr[i+k][j+l];
                sqr_cnt++;
            }
        }
    }
}

bool dfs(int d,LL s){
    LL t = s,sel = -1;
    int mind = 0;
    for(int i = 0;i < sqr_cnt;i++){
        if((t&sqr[i]) == sqr[i]){
            t ^= sqr[i];
            mind++;
            if(sel == -1) sel = sqr[i];
        }
    }
    if(sel == -1) return true;
    if(d+mind > maxd) return false;

    for(int j = 1;j <= edge_cnt;j++){
        if(sel & get_LL(j))
            if(dfs(d+1,s^(get_LL(j)))) return true;
    }

    return false;
}

int solve(){
    LL s = ((LL)1<<edge_cnt)-1;
    int t,x;
    scanf("%d",&t);
    while(t--){
        scanf("%d",&x);
        s ^= get_LL(x);
    }

    for(maxd = 0;;maxd++){
        if(dfs(0,s)) break;
    }
    return maxd;
}

int main()
{
    int iCase;
#ifdef GEH
    freopen("helloworld.01.inp","r",stdin);
#endif
    scanf("%d",&iCase);
    while(iCase--){
        init();
        printf("%d
",solve());
    }
    return 0;
}