目录:
- 个人理解
- 做题步骤
- 例题的状态转移方程
一、个人理解:
-
树形DP简介:
树形DP就是在树上的DP,一般用递归实现。有两种实现的递归方式:
- 叶 ( ightarrow) 根:先更新了叶节点的信息,在回溯回去更新父亲节点的信息。(eg. P1352 没有上司的舞会 )
- 根 ( ightarrow) 叶:先从叶节点往根节点DFS一遍(预处理)了以后,在重新往下更新。(不常用)
-
前提:本题是一棵树或是一个森林(非常重要!)
-
难点:
- 状态转移方程
- 边界条件
- 剪枝优化
- 细节(左子节点,右子节点,父节点)
-
注意事项:
- 建无向图:若建有向图,可以不判断父节点,但若是从子节点更新到父节点,则需要从子到父,不太方便。可以直接建无向图,记录一下
fa[],再判断一下即可。 e[]开两倍空间。- 递归一定要写边界条件。
- 建无向图:若建有向图,可以不判断父节点,但若是从子节点更新到父节点,则需要从子到父,不太方便。可以直接建无向图,记录一下
二、做题步骤:
-
判断此题是否是一棵树或一个森林。(前提)
-
判断此题为二叉树还是多叉树。(都用前向星储存)
若是二叉树则用
lc[],rc[],fa[]记录;若是多叉树则判断可否化为二叉树,若不能则直接用
fa[] -
推状态转移方程
-
化为DFS形式。(在空间允许的情况下可以记搜)
三、常见的状态转移方程:
-
父节点不能和子节点同时选( P1352 没有上司的舞会)
定义 (f(i)(0/1)) 表示 (i) 点的最优解,(0) 表示 (i) 不选,(1) 表示 (i) 点要选。(crit(i)) 表示选择 (i) 可以获得的价值。(son(i)) 表示 (i) 的子节点。
若 (i) 点要选,则 (i) 的子节点都不能选,故状态转移方程为:
[f(i)(1)=sum_{jin son(i)}f(j)(0)+crit(i) ]若 (i) 点不选,则 (i) 的子节点可选可不选,故状态转移方程为:
[f(i)(0)=sum_{jin son(i)}max{f(j)(0),f(j)(1)} ]下图为洛谷秋令营的课件讲解:

-
树形分组背包(1)(P2014 选课)
定义 (f(i)(j)) 表示 (i) 点选择 (j) 种课程的最优解。 (crit(i))表示选择 (i) 可以获得的价值。(son(i)) 表示 (i) 的子节点。
有分组背包标准模型可得,状态转移方程为:
[f(i)(k)=max_{l=0}^{k-1} {f(i)(k-l)+f(j)(l)}(kin[1,m+1],jin son(i)) ][f(i)(1)=crit(i) ]关键代码片段如下:
DP(1)//调用 void DP(int fr) { for(int i=head[fr];i;i=e[i].next)//分组背包中的枚举总组数 { int to=e[i].to; if(to==fa[fr]) continue; DP(to); for(int j=m+1;j>=1;j--)//分组背包中的枚举背包容量 { for(int k=0;k<j;k++)//分组背包中的枚举每组中的物品个数 { dp[fr][j]=max(dp[fr][j],dp[fr][j-k]+dp[to][k]); } } } } -
二叉树去有限条边后总边权最大值(P2015 二叉苹果树)
定义 (f(i)(j)) 为 (i) 点去 (j) 条边的最优解。(crit(i,j)) 为 (i) 点到 (j) 点的边权。(son(i)) 表示 (i) 的子节点。
则 (i) 点去 (j) 条边的最优解为 (i) 点的子节点去 (k) 条边的最优解、(i) 点去 (j-i-1) 条边的最优解与 (i) 到 (i) 的子节点的边权的和的最大值。
故状态转移方程为:
[f(i)(k)=max_{l=0}^{l-1} {f(i)(k-l-1)+f(j)(l)+crit(i,j)} ][(kin [1, ext{q}],jin son(i)) ]关键代码片段如下:
DP(1,0);//调用 void DP(int fr,int fa) { for(int i=head[fr];i;i=e[i].next) { int to=e[i].to; int v=e[i].v; if(to==fa) continue; DP(to,fr); for(int j=Q;j>=1;j--) { for(int k=j-1;k>=0;k--) { dp[fr][j]=max(dp[fr][j],dp[fr][j-k-1]+dp[to][k]+v); } } } } -
树的最小覆盖集(P2016战略游戏 )
注:此题可用二分图匹配实现:
这题其实有几种方法,其中比较显而易见的或许是树形dp吧,楼下有很多大佬已经解释过了,(这里就不再说了),仔细一看题就可以发现这是一个典型的最小点覆盖。
最小点覆盖指的是在一个图中:一个点覆盖与之连接的边,求用最少的点可以覆盖。
这和题目要求一模一样。同时还有一个定理,最小点覆盖=最大匹配数。如果是无向图则/2。————摘自 pengym 的题解
定义 (f(i)(0/1)) 为 (i) 点的最优解,(0) 表示 (i) 不选,(1) 表示 (i) 要选。(son(i)) 表示 (i) 的子节点。
若 (i) 点要选,则 (i) 点的子节点可选可不选,最后还要加上自己一个节点,故状态转移方程为:
[f(i)(1)=sum_{jin son(i)}min{f(j)(0),f(j)(1)}+1 ]若 (i) 点不选,则 (i) 点的子节点必须选,故状态转移方程为:
[f(i)(0)=sum_{jin son(i)}f(j)(1) ]特别提醒: (f(i)(0/1)) 必须初始化为 $+infty $
-
树形分组背包(2)(P1273 有线电视网)
定义 (f(i)(j)) 为 (i) 点保留 (j) 个叶节点的最优解。(crit(i,j)) 为 (i) 点到 (j) 点的边权。(son(i)) 表示 (i) 的子节点。(size(i)) 表示 (i) 节点的子树大小。( ext{E}_{ ext{Leaf}}) 为树的叶节点的集合。( ext{E}_{ ext{All}}) 为树的所有节点的集合。(value(i)) 为 (i) 点所需的费用((iin ext{E}_{ ext{Leaf}}) )。
则 (i) 点的最优解为子节点保留 (k) 个叶节点的最优解再加上 (i) 点能保留 (j-k) 个叶节点的最优解减去边权。
最后只需统计可以更新到的最大值。
故状态转移方程为:
[f(i)(k)=max_{jin son(i)}{f(i)(k-l)+f(j)(l)-crit(i,j)} ][(kin[0,size(i)],lin [0,min{k,size(j)}]) ][f(i)(0)=0(iin ext{E}_{ ext{All}}),f(i)(1)=value(i)(iin ext{E}_{ ext{Leaf}}),size(i)=1(iin ext{E}_{ ext{Leaf}}) ]关键代码如下:
DP(1,-1);//调用 void DP(int fr,int fa) { for(int i=head[fr];i;i=e[i].next) { int to=e[i].to; if(to==fa) continue; DP(to,fr); siz[fr]+=siz[to]; } for(int i=head[fr];i;i=e[i].next) { int to=e[i].to; int v=e[i].v; if(to==fa) continue; for(int j=siz[fr];j>=0;j--) { for(int k=0;k<=min(j,siz[to]);k++) { dp[fr][j]=max(dp[fr][j],dp[fr][j-k]+dp[to][k]-v); } } } } for(int i=m;i>=0;i--)//统计最终答案 { if(dp[1][i]>=0) { printf("%lld ",i); return 0; } }特别提醒:
- (f(i)(j)) 一定要初始化为$-infty $ ,并且 (f(i)(0)) 、 (f(i)(1) (iin ext{E}_{ ext{Leaf}})) 和 (size(i)(iin ext{E}_{ ext{Leaf}})) 一定要按上面写的初始化。
- 在输入时,千万不要搞错 (i) 和 (j) 。
-
基环树DP(P2607 [ZJOI2008]骑士)
本题的DP模型同 P1352 没有上司的舞会。本题的难点在于如何把基环树DP转化为普通的树上DP。
考虑断边和换根。先找到其中的一个环,在上面随意取两个点, 断开这两个点的边,使其变为一棵普通树。以其中的一点为树根做树形DP,再以另一点为树根再做一次树形DP,因为相邻的两点不能同时选,所以最后统计一下 (f(i)(0)) 与 (g(j)(0)) 的最大值即可。
定义 (f(i)(0/1)) 为第一次树形DP的 (i) 点的最优解,(g(i)(0/1)) 为第二次树形DP的 (i) 点的最优解。$ ext{Ans} $ 为一次基环树DP的答案。( ext{E}_ ext{Circle}) 为基环树的环上的点的集合。
故一次基环树DP的答案为:
[ ext{Ans}=max{f(i)(0),g(j)(0)} ][(i,jin ext{E}_ ext{Circle},i eq j) ]下图为洛谷秋令营的课件讲解:
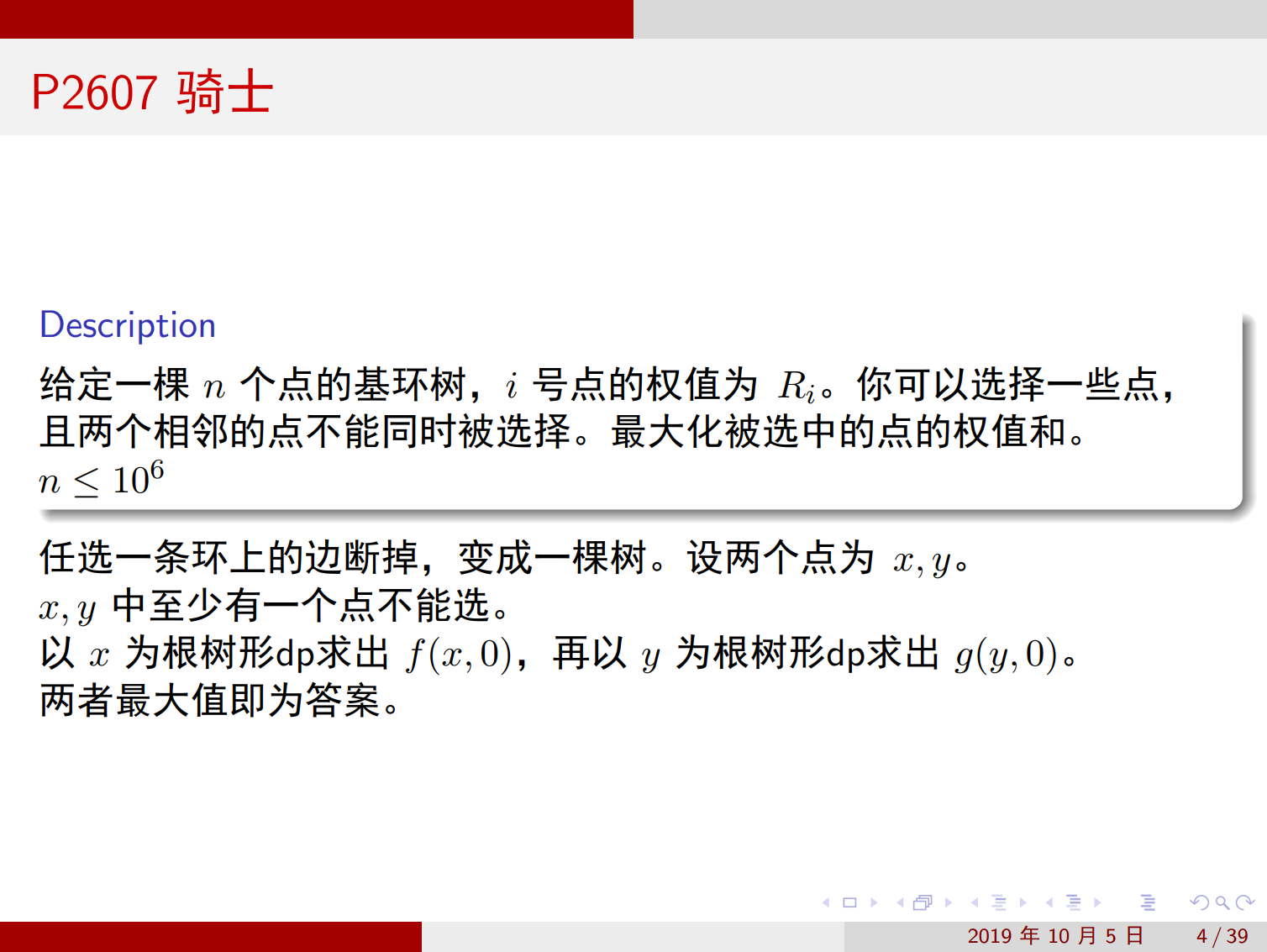
关键代码如下:
void covertree(int fr)//寻找基环树 { used[fr]=1; for(int i=head[fr];i;i=e[i].next) { int to=e[i].to; if(used[to]==0) { covertree(to); } } } void findcir(int fr,int fa)//寻找基环树中的环 { if(flag) return ; vis[fr]=1; for(int i=head[fr];i;i=e[i].next) { int to=e[i].to; if(vis[to]==0) { findcir(to,fr); }else if(to!=fa) { fri=fr;//第一个点 toi=to;//第二个点 E=i;//边的编号 flag=1; return ; } } } void DPf(int fr)//以其中的一点为树根做树形DP { visf[fr]=1; f[fr][1]=crit[fr]; for(int i=head[fr];i;i=e[i].next) { int to=e[i].to; if(visf[to]==0&&(i^1)!=E)//保证不会选到第一个点和第二个点,相当于断边 { DPf(to); f[fr][0]+=max(f[to][0],f[to][1]); f[fr][1]+=f[to][0]; } } } void DPg(int fr)//再以另一点为树根再做一次树形DP { visg[fr]=1; g[fr][1]=crit[fr]; for(int i=head[fr];i;i=e[i].next) { int to=e[i].to; if(visg[to]==0&&(i^1)!=E) { DPg(to); g[fr][0]+=max(g[to][0],g[to][1]); g[fr][1]+=g[to][0]; } } } for(int i=1;i<=n;i++)//调用+统计答案 { if(used[i]==1) continue; covertree(i); flag=0; findcir(i,-1); DPf(fri); DPg(toi); ans+=max(f[fri][0],g[toi][0]); }特别注意:
- 本题是基环树森林,而不是单棵基环树,故要反复寻找覆盖基环树,最后将所有答案加起来。
- 因为要断边,所以前向星计数器
ei一定要初始化为 1。 - 用多个数组标记(
used[],vis[],visf[],visg[])。 - 一定要注意
f,g和fr,to,不要手快打错了。