CLRS 16.2-2 请给出一个解决0-1背包问题的运行时间为O(nW)的动态规划方法,其中,n为物品的件数,W为窃贼可放入他的背包中的物品中的最大重量。
我们有n种物品,物品j的重量为wj,价格为pj。我们假定所有物品的重量和价格都是非负的。背包所能承受的最大重量为W。
如果限定每种物品只能选择0个或1个,则问题称为0-1背包问题。可以用公式表示为:
- maximize
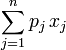
- subject to

方法一:
采用最原始的递归方法,公式为
V(1,...,n) = max(vk + V(1,...,k-1,k+1,...,n));时间复杂度为O(2n),很多子问题被重复计算。
 View Code
View Code
1 #include <stdio.h> 2 #include <stdlib.h> 3 4 //每件物品的价值和重量 5 typedef struct goods_t 6 { 7 int weight; 8 int value; 9 }goods; 10 11 //删除第i个元素后的所有元素 12 goods* remain_data(goods* data, const int n, const int i) 13 { 14 goods* remain = (goods*)malloc((n-1)*sizeof(goods)); 15 int j; 16 int count = 0; 17 for (j = 0; j < n; j++) 18 { 19 if (j != i) 20 remain[count++] = data[j]; 21 } 22 return remain; 23 } 24 25 //递归 26 int recursive(goods* data, const int n, int weight) 27 { 28 int max = 0; 29 int i; 30 for (i = 0; i < n; i++) 31 { 32 if (data[i].weight <= weight) 33 { 34 int tmp = data[i].value + recursive(remain_data(data, n, i), n - 1, weight - data[i].weight); 35 if (tmp > max) 36 max = tmp; 37 } 38 } 39 return max; 40 } 41 42 int main() 43 { 44 //输入最大重量 45 int max_weight; 46 scanf("%d", &max_weight); 47 //输入物品件数及其重量和价值 48 int num; 49 scanf("%d", &num); 50 int n = num; 51 goods* data = (goods*)malloc(n*sizeof(goods)); 52 53 goods g; 54 while (num--) 55 { 56 scanf("%d%d", &(g.weight), &(g.value)); 57 data[n-num-1] = g; 58 } 59 printf("%d\n", recursive(data, n, max_weight)); 60 return 0; 61 }
方法二:
我们假定w1, ..., wn和W都是正整数。我们将在总重量不超过Y的前提下,前j种物品的总价格所能达到的最高值定义为A(j, Y)。
A(j, Y)的递推关系为:
- A(0, Y) = 0
- A(j, 0) = 0
- 如果wj > Y, A(j, Y) = A(j - 1, Y)
- 如果wj ≤ Y, A(j, Y) = max { A(j - 1, Y), pj + A(j - 1, Y - wj) }
最后一个公式的解释:总重量为Y时背包的最高价值可能有两种情况,第一种是在Y重量下,可以在前j - 1个物品中得到最大价值,这对应于表达式A(j - 1,Y)。第二种是包含了第j个物品,那么对于前j-1个物品,可以在重量为Y-wj的情况下找到最大价值,综合起来就是pj + A(j - 1, Y - wj)。
 View Code
View Code
1 #include <stdio.h> 2 #include <stdlib.h> 3 4 //每件物品的价值和重量 5 typedef struct goods_t 6 { 7 int weight; 8 int value; 9 }goods; 10 11 //动态规划 12 int dp(goods* data, const int n, const int weight) 13 { 14 int A[n+1][weight+1]; 15 int i; 16 //如果i=0或者w=0 17 for (i = 0; i < n+1; i++) 18 A[i][0] = 0; 19 for (i = 0; i < weight+1; i++) 20 A[0][i] = 0; 21 int w; 22 for (i = 1; i <= n; i++) 23 { 24 for (w = 1; w <= weight; w++) 25 { 26 if (data[i-1].weight > w) 27 A[i][w] = A[i-1][w]; 28 else 29 { 30 A[i][w] = A[i-1][w] > (data[i-1].value + A[i-1][w-data[i-1].weight]) ? A[i-1][w] : (data[i-1].value + A[i-1][w-data[i-1].weight]); 31 } 32 } 33 } 34 return A[n][weight]; 35 } 36 37 int main() 38 { 39 //输入最大重量 40 int max_weight; 41 scanf("%d", &max_weight); 42 //输入物品件数及其重量和价值 43 int num; 44 scanf("%d", &num); 45 int n = num; 46 goods* data = (goods*)malloc(n*sizeof(goods)); 47 48 goods g; 49 while (num--) 50 { 51 scanf("%d%d", &(g.weight), &(g.value)); 52 data[n-num-1] = g; 53 } 54 printf("%d\n", dp(data, n, max_weight)); 55 return 0; 56 }
参考:维基百科 背包问题
CLRS 16.2-6 说明如何在O(n)时间内解决部分背包问题
W表示背包所容最大重量
1.将pi = vi / wi 计算出来,然后找出其中间值m,时间为O(n),这里只是找到m,不用排序,所以复杂度仅为O(n)。(用快排的思想,大体是这样的,选定一个数,将集合分为两半,一个集合大于它,一个集合小于它,若两个集合相等,则这个数就是中位数,否则进入大集合里面继续找,每次都对半,n/2 + n/4 + n/8 + ... = O(n))
2.找到中位数之后,将所有物品按>m, =m, <m分为三个集合,分别为L、M、N,计算集合L内所有物品加起来的总重量WL,
2.1WL=W,则WL集合内物品即为所求
2.2若WL < W,那再在M集合里添加物品,若还是不够,就在N集合里找,在N集合里找的时候,重复步骤1,2。
2.3若WL > W,那就在L集合里重复步骤1,2.
CLRS 16.2-7
A和B都按升序或者都按降序排列即可。
任意选取两个元素ai,aj,bi,bj,
计算aibi*ajbj,同时计算aibj*ajbi,两式相除,不管是升序还是降序,都是aibi*ajbj大。由于是任意选取的,推广开来,因而总的也最大。
