输入一个整型数组,实现一个函数来调整该数组中的数字的顺序,使得所有偶数位于数组的前半部分,所有奇数位于数组的后半部分,希望时间复杂度尽量小
第一种思路,从前往后遍历,找到第一个是偶数的,和数组第一位互换;以此类推;
最坏的情况是全是偶数,依然还互换多次,可以增加判断条件 brr[x] 是奇数才进行互换(减少互换次数,但是增加了处理时间,这是因为整型数据互换的成本较低,针对大内存数据互换另当别论)
int brr[] = {1,2,3,4,5,6}; long time1 = System.nanoTime(); int x = 0; for (int i = 0; i < brr.length; i++) { if (brr[i] % 2 == 0 ) { //if (brr[i] % 2 == 0 && brr[x] % 2 != 0 ) { int temp = brr[i]; brr[i] = brr[x]; brr[x] = temp; x++; } } System.out.println(Arrays.toString(brr)); System.out.println(System.nanoTime()-time1);
第二种思路,前半部分的奇数和后半部分的偶数互换位置,判断较多,互换次数少
int brr[] = {1,2,3,4,5,6}; long time2 = System.nanoTime(); for (int i = 0, j = brr.length - 1; i < j; i++, j--) { while (brr[i] % 2 == 0 && i < j) { i++; } while (brr[j] % 2 != 0 && j > 0) { j--; } if(i<j){ int temp = brr[i]; brr[i] = brr[j]; brr[j] = temp; } } System.out.println(System.nanoTime() - time2);
出于好奇,测试一下两种方法的耗时
public static void main(String[] args) { int count = 10000; long swap = 0l; long comp = 0l; for (int c = 0; c < count; c++) { int[] arr2 = getInts(); long start2 = System.nanoTime(); int x = 0; for (int i = 0; i < arr2.length; i++) { if (arr2[i] % 2 == 0) { int temp = arr2[i]; arr2[i] = arr2[x]; arr2[x] = temp; x++; } } swap += System.nanoTime() - start2; /////////////////////////////////////////////////////// int[] arr = getInts(); long start = System.nanoTime(); int max = arr.length - 1; for (int i = 0, j = max; i < j; i++, j--) { while (arr[i] % 2 == 0 && i < max) { i++; } while (arr[j] % 2 != 0 && j > 0) { j--; } if (i < j) { int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } } comp += System.nanoTime() - start; /////////////////////////////////////////////////////// } System.out.println("COMP:" + comp / count); System.out.println("SWAP:" + swap / count); } private static int[] getInts() { int[] arr = new int[10000]; for (int i = 0; i < arr.length; i++) { arr[i] = 2; } return arr; }
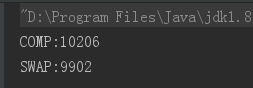
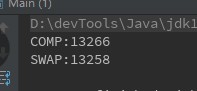
有点像经典的“时间和空间” 问题
void swap(int a, int b) //空间换时间 { int c; c=a; a=b; b=a; } void swap(int a, int b) //时间换空间 { a=a+b; b=a-b; a=a-b; }
PS : 有意思的是,多次调用其中某一种方法多次,耗时都是这种规律,第一次出现第二大值,但是中间必然出现一次最大值,其中究竟还不得知,估计要深入计算机原理去看,赋值操作和比较操作的耗时关系
如发现问题,希望各路大神尽情指出。