六、Sklearn线性回归

参考url:

https://jakevdp.github.io/PythonDataScienceHandbook/05.06-linear-regression.html

1、简单线性回归

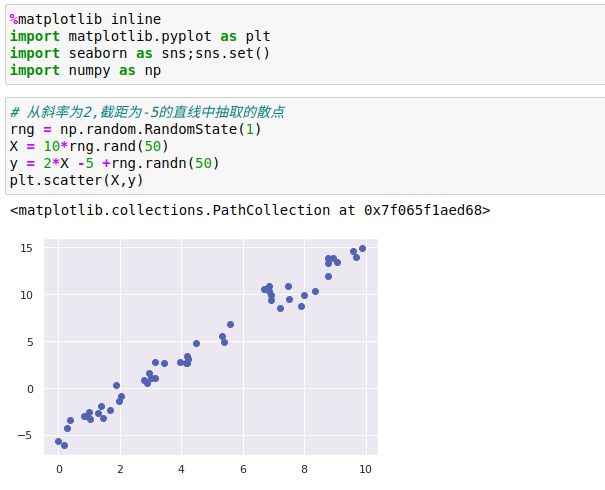
　　最广为人知的线性模型——将数据拟合成一条直线。

　　直线拟合的模型方程为y=ax+b，其中a是直线斜率，b是直线截距。

　　

　　

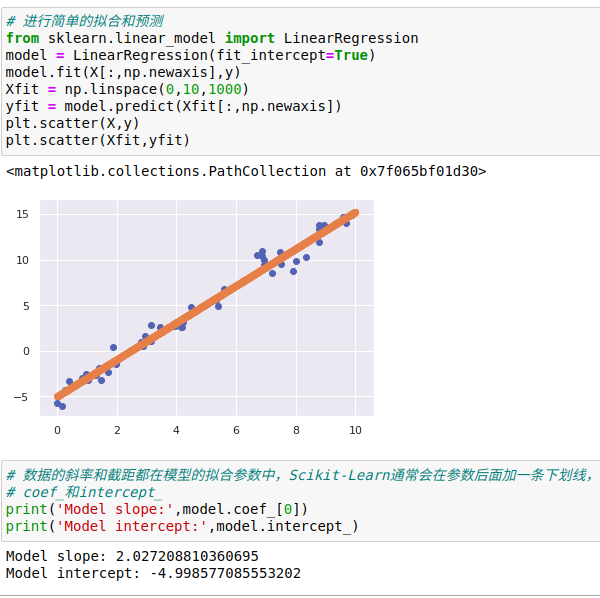
 　　LinearRegression评估器除了简单的直线拟合，它还可以处理多维度的线性回归模型：

　　　　y=a0+a1x1+a2x2+...里面有多个x变量

　　从几何学的角度看，这个模型是拟合三维空间中的一个平面，或者是为更高维度的数据点拟合一个超平面。

　　

 　　通过这种方式，就可以用一个LinearRegression评估器拟合数据的回归直线、平面和超平面了。

　　

2、基函数回归

　　通过基函数对元素数据进行交换，从而将变量间的线性回归模型转换为非线性回归模型。

　　基函数回归的多维模型是：y=a₀+a₁x₁+a₂x₂+a₃x₃+...，其中一维的输入变量x转换成了x1、x2和x3。让x_n = f_n(x)，这里的f_n()是转换数据的函数。

　　假如f_n(x)=xⁿ，那么模型就会变成多项式回归：y=a₀+a₁x+a₂x^₂+a₃x^₃+...这个模型仍然是一个线性模型，也就是说系数aⁿ彼此不会相乘或相除。

　　我们其实是将一维的x投影到了高维空间,因此通过线性模型就可以拟合出x与y间更复杂的关系。

　　1、多项式基函数

　　　　

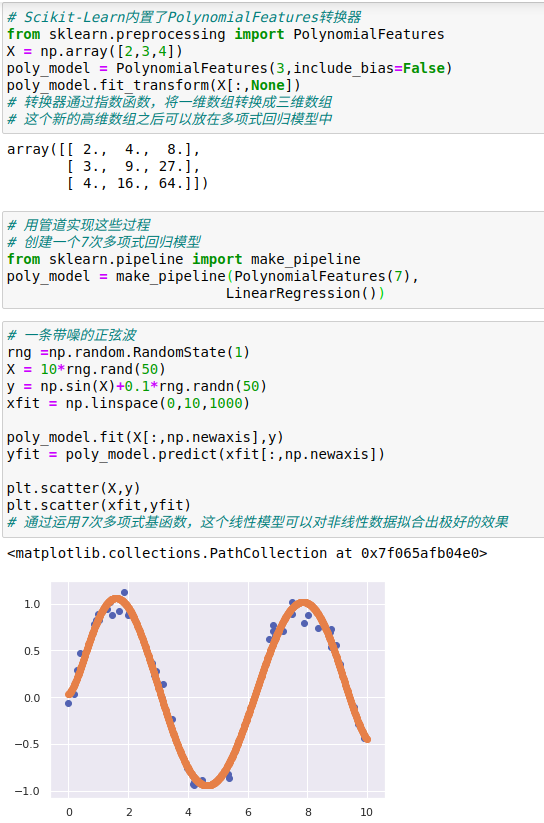
　　2、高斯基函数

　　　　有一种常用的拟合模型方法使用的并不是一组多项式基函数，而是一组高斯基函数。

　　　　Scikit-Learn并没有内置高斯基函数，我们可以自己写一个转换器来创建高斯基函数。

　　　　

 　　　　

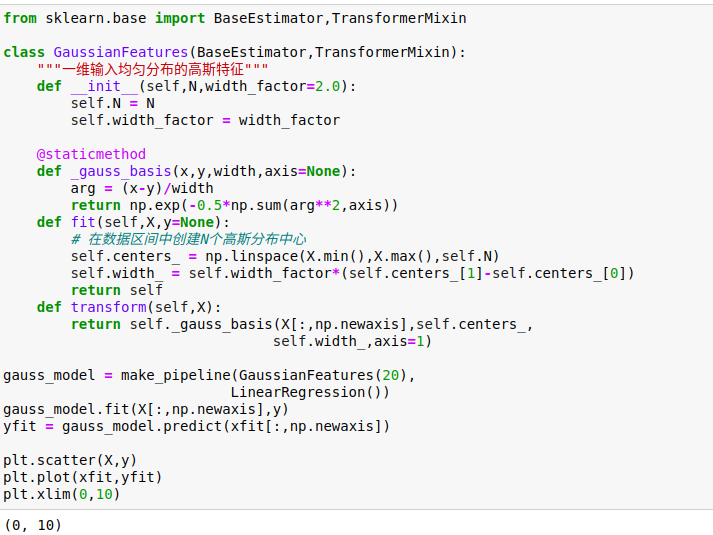
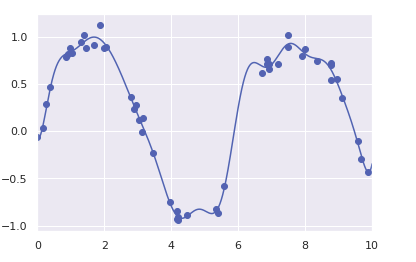
3、正则化

　　虽然在线性回归模型中引入基函数会让模型变得更加灵活，但是也很容易造成过拟合。

　　

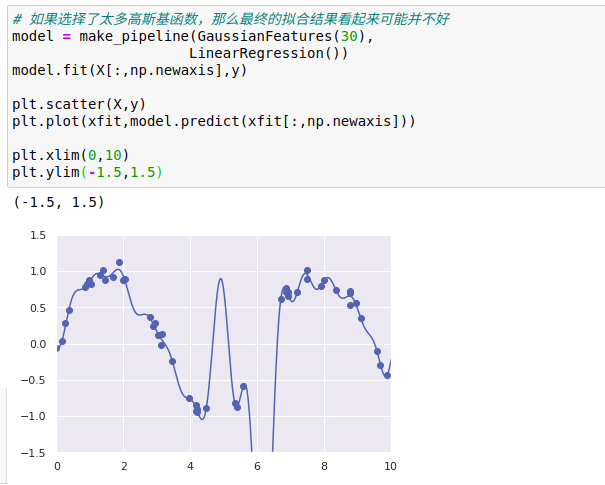
　　如果将数据投影到30维的基函数上，模型就会变得过于灵活，从而能够适应数据中不同位置的异常值。

　　 

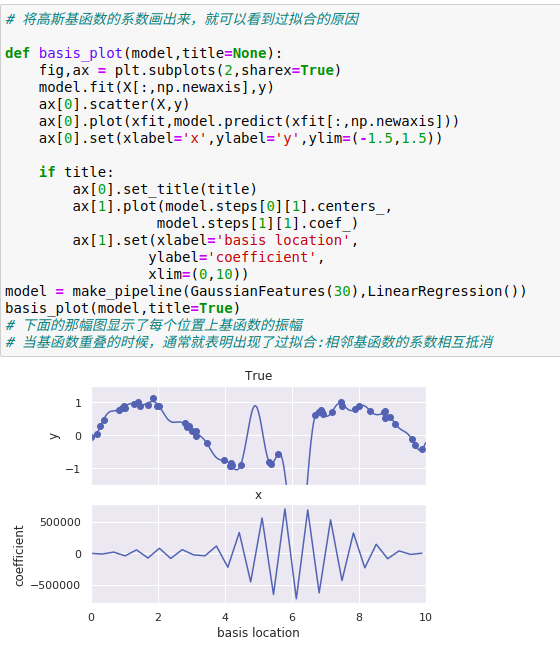
　　如果对较大的模型参数进行惩罚（penalize）,从而抑制模型剧烈波动，就可以解决相邻基函数的系数相互抵消而出现过拟合的问题

　　这中惩罚机制被称为正则化（regularization）：

　　　　１、岭回归（L₂范数正则化）

　　　　　　正则化最常见的形式可能就是岭回归（ridge regression，或者L₂范数正则化），有时也被称为吉洪诺夫正则化（Tikhonov regularization）。

　　　　　　其处理方法是对模型系数平方和（L₂范数）进行惩罚，模型拟合的惩罚项为：

　　　　

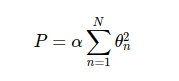
　　　　　　其中，α是一个自由参数，用来控制惩罚的力度。

　　　　　　这种带惩罚项的模型内置在Scikit-Learn的Ridge评估器中

　　　　　　 

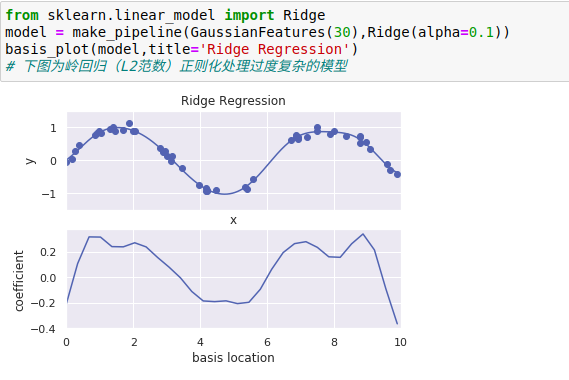
 　　　　　　参数α是控制最终模型复杂度的关键，如果α→ 0，那么模型就恢复到标准线性回归结果，如果α→ ∞，那么所有模型响应都会被压制。

　　　　　　岭回归的一个重要优点是，他可以非常高效地计算——因此相比原始的线性回归模型，几乎没有消耗更多的计算资源。

　　　　2、Lasso正则化（L₁范数）

　　　　　　另一种常用的正则化被称为Lasso，其处理方法是对模型系数绝对值的和（L₁范数）进行惩罚：

　　　　　　

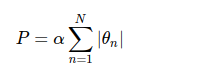
　　　　　　虽然它在形式上非常接近岭回归，但是其结果与岭回归差别很大。

　　　　　　由于其几何特性，Lasso正则化倾向于构建稀疏模型，也就是说，它更喜欢将模型系数设置为0

　　　　　　

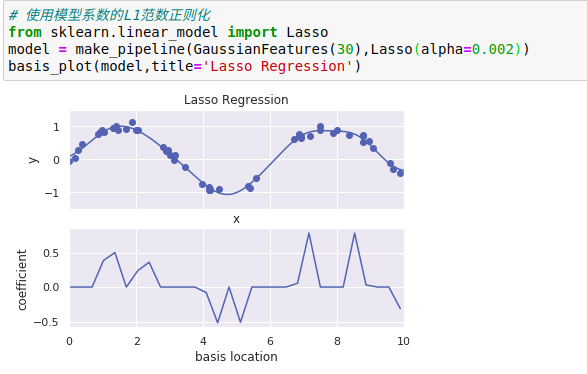
 　　　　　　通过Lasso回归惩罚，大多数基函数的系数都变成了0，所以模型变成了原来基函数的一小部分。

　　　　　　与岭回归正则化类似，参数α控制惩罚力度，可以通过交叉检验来确定。