线段树
1、线段树是一棵二叉搜索树,它储存的是一个区间的信息。
2、每个节点以结构体的方式存储,结构体包含以下几个信息:
- 区间左端点、右端点;(这两者必有)
- 这个区间要维护的信息(事实际情况而定,数目不等)。
3、线段树的基本思想: 二分 。
4、线段树一般结构如图所示:
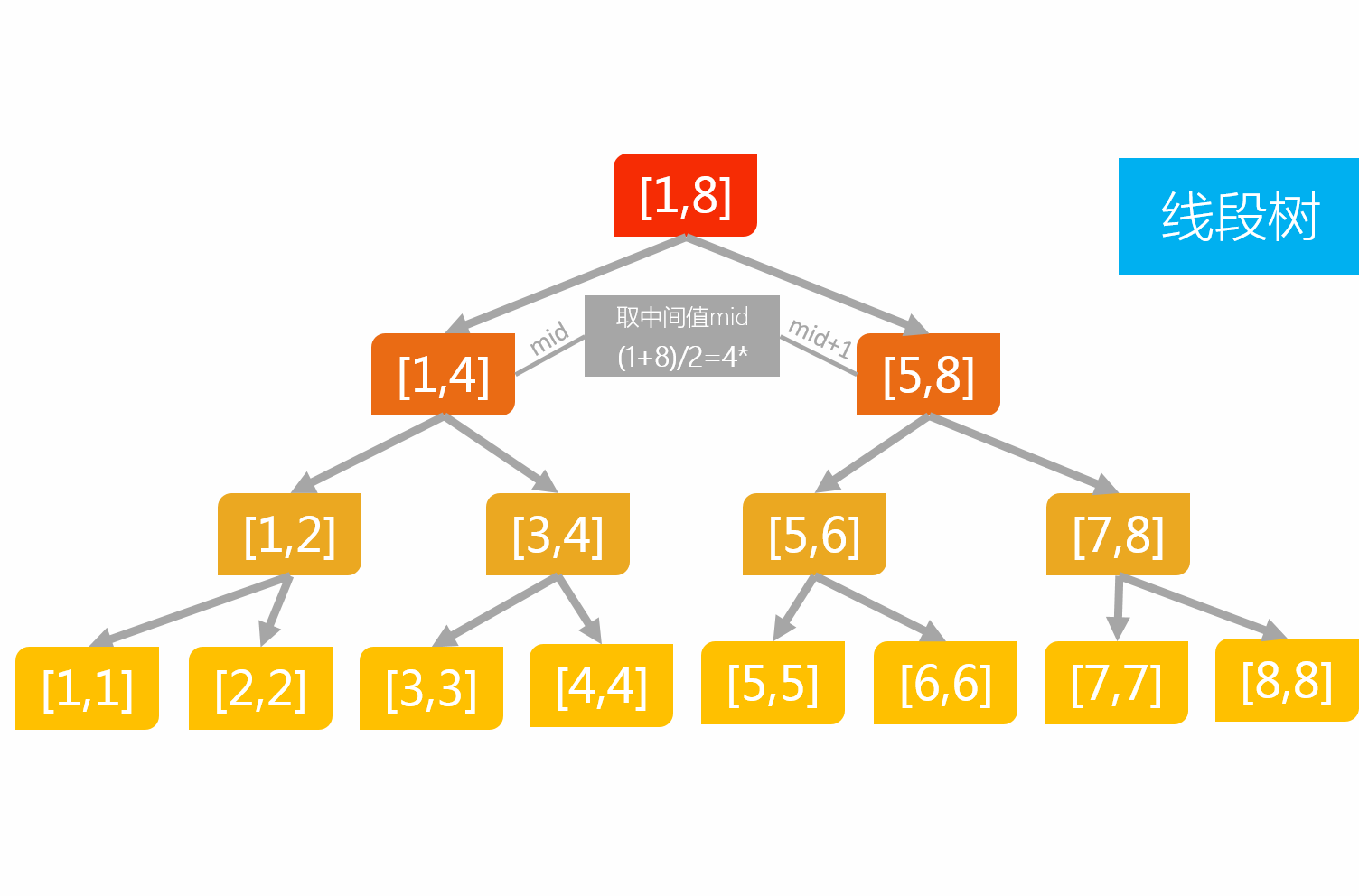

每个节点的左孩子区间范围为[l,mid],右孩子为[mid+1,r]
线段树的基础操作主要有5个:
建树、单点查询、单点修改、区间查询、区间修改。
(以下均为求和操作)
1 struct node{ 2 int l,r,w;//l左区间,r右区间,w区间和 3 }xdtree[4*n];//n个数
一、建树
a、对于二分到的每一个结点,给它的左右端点确定范围。
b、如果是叶子节点,存储要维护的信息。
c、状态合并。
!!:: 4倍空间
不要漏了return语句
1 void build(int l,int r,int k){//k是根节点的下标 2 3 xdtree[k].l=l; 4 xdtree[k].r=r; 5 6 if(l==r){ 7 8 cout<<xdtree[k].w;//n个数的和 9 return; 10 } 11 12 int m=(l+r)/2; 13 build(l,m,2*k); 14 build(m+1,r,2*k+1); 15 xdtree[k].w=xdtree[2*k].w+xdtree[2*k+1].w; 16 17 }
二、单点查询
1 void ask(int k){//k一般为1,x是查询点 2 int ans; 3 4 if(xdtee[k].l==xdtree[k].r) 5 ans=xdtree[k].w,return; 6 7 int m=(xdtree[k].l + xdtree[k].r)/2; 8 if(x<=m) ask(k*2) ;//若目标靠左,递归左儿子 9 else ask(k*2+1);//目标靠右。递归右儿子 10 11 }
三、单点修改
第x个数加上y

1 void add(int k){ 2 3 if(xdtree[k].l==xdtree[k].r) 4 xdtree[k].w+=y,return; 5 6 int m=(xdtree[k].l+xdtree[k].r)/2; 7 if(x<=m) add(k*2); 8 else add(k*2+1); 9 10 xdtree[k].w=xdtree[k*2].w+xdtree[k*2+1].w;//更新包含k的节点 11 } 12
四、区间查询
查询[ x , y ]的值


mid=(l+r)/2
y<=mid ,即 查询区间全在,当前区间的左子区间,往左孩子走
x>mid 即 查询区间全在,当前区间的右子区间,往右孩子走
否则,两个子区间都走
1 void ask_(int k){ 2 3 if(xdtree[k].l>=x&&xdtree[k].r<=y) 4 ans += xdtree[k].w,return; 5 6 int m=(xdtree[k].l+xdtree[k].r)/2; 7 8 if(y>m) ask_(k*2+1); 9 if(x<=m) ask_(k*2); 10 11 } 12
五、区间修改

修改的时候只修改对查询有用的点。
引入
懒标记:存储到这个节点的修改信息,暂时不把修改信息传到子节点。就像家长扣零花钱,你用的时候才给你,不用不给你。
a.原结构体中增加新的变量,存储这个懒标记。
b.递归到这个节点时,只更新这个节点的状态,并把当前的更改值累积到标记中。注意是累积,可以这样理解:过年,很多个亲戚都给你压岁钱,但你暂时不用,所以都被你父母扣下了。
c.什么时候才用到这个懒标记?当需要递归这个节点的子节点时,标记下传给子节点。这里不必管用哪个子节点,两个都传下去。就像你如果还有妹妹,父母给你们零花钱时总不能偏心吧
d.下传操作:
3部分:①当前节点的懒标记累积到子节点的懒标记中。
②修改子节点状态。在引例中,就是原状态+子节点区间点的个数*父节点传下来的懒标记。
这就有疑问了,既然父节点都把标记传下来了,为什么还要乘父节点的懒标记,乘自己的不行吗?
因为自己的标记可能是父节点多次传下来的累积,每次都乘自己的懒标记造成重复累积
③父节点懒标记清0。这个懒标记已经传下去了,不清0后面再用这个懒标记时会重复下传。就像你父母给了你5元钱,你不能说因为前几次给了你10元钱, 所以这次给了你15元,那你不就亏大了。
懒标记下穿代码:f为懒标记,其余变量与前面含义一致。
void down(int k)//标记下传 { xdtree[k*2].f+=xdtree[k].f; xdtree[k*2+1].f+=xdtree[k].f; xdtree[k*2].w+=xdtree[k].f*(xdtree[k*2].r-xdtree[k*2].l+1); xdtree[k*2+1].w+=xdtree[k].f*(xdtree[k*2+1].r-xdtree[k*2+1].l+1); xdtree[k].f=0; }
1 void add_(int k){ 2 3 if(xdtree[k].l>=a&&xdtree[k].r<=b) 4 { 5 xdtree[k].w+=x*(xdtree[k].r-xdtree[k].l+1); 6 xdtree[k].f+=x; 7 return; 8 } 9 if(xdtree[k].f) down(k); 10 int m=(xdtree[k].l+xdtree[k].r)/2; 11 if(y>=m) add_(k*2); 12 if(x<m) add_(k*2+1); 13 xdtree[k].w=xdtree[k*2].w+xdtree[k*2+1].w; 14 }
因为引入了懒标记,很多用不着的更改状态存了起来,这就会对区间查询、单点查询造成一定的影响。
所以在使用了懒标记的程序中,单点查询、区间查询也要像区间修改那样,对用得到的懒标记下传。其实就是加上一句if(tree[k].f) down(k),其余不变。
引入了懒标记的单点查询代码:
void ask(int k)//单点查询
{
if(xdtree[k].l==xdtree[k].r)
{
ans=xdtree[k].w;
return ;
}
if(xdtree[k].f) down(k);//懒标记下传,唯一需要更改的地方
int m=(xdtree[k].l+xdtree[k].r)/2;
if(y>m) ask(k*2+1);
else ask(k*2);
}
引入了懒标记的区间查询代码:
void ask_(int k)//区间查询
{
if(xdtree[k].l>=x&&xdtree[k].r<=y)
{
ans+=xdtree[k].w;
return;
}
if(xdtree[k].f) down(k)//懒标记下传,唯一需要更改的地方
int m=(xdtree[k].l+xdtree[k].r)/2;
if(y>m) ask_(k*2+1);
if(x<=m) ask_(k*2);
}
LAST 空间优化
http://www.cppblog.com/MatoNo1/archive/2015/05/05/195857.html
参考:https://www.cnblogs.com/TheRoadToTheGold/p/6254255.html
