sklearn---SVM

 

一、用SVM实现二分类

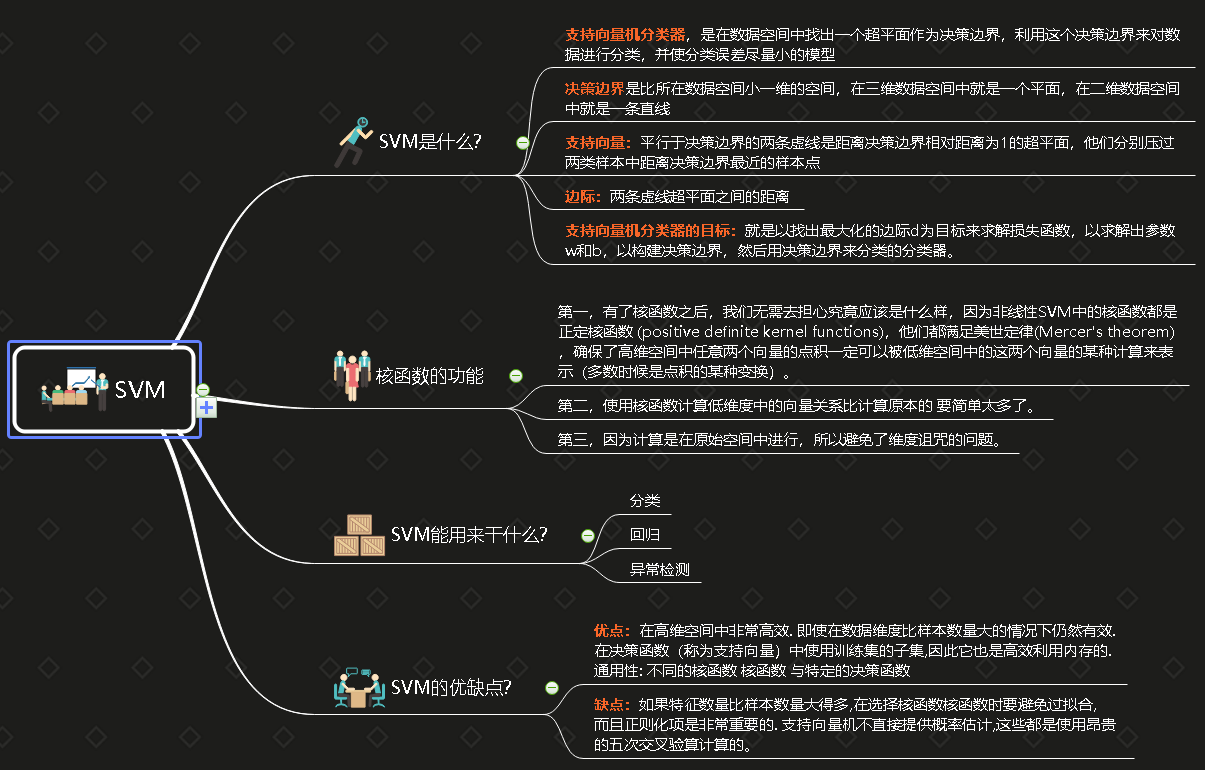
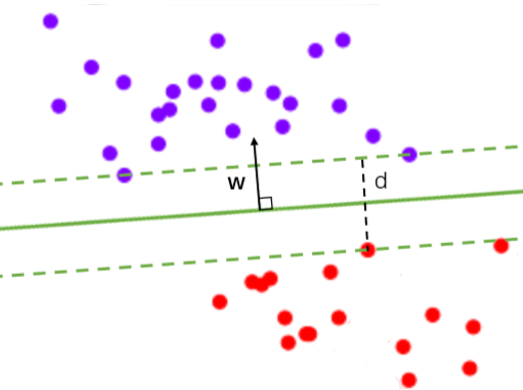
支持向量机分类器，是在数据空间中找出一个超平面作为决策边界，利用这个决策边界来对数据进行分类，并使分类误差尽量小的模型

                                                 

 

class sklearn.svm.SVC(C=1.0, kernel=’rbf’, degree=3, gamma=’auto_deprecated’, coef0=0.0, shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1,decision_function_shape=’ovr’, random_state=None)

“kernel"在sklearn中可选以下几种选项

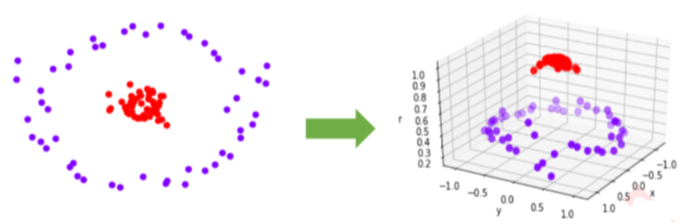
可以看出，除了选项"linear"之外，其他核函数都可以处理非线性问题。多项式核函数有次数d，当d为1的时候它 就是再处理线性问题，当d为更高次项的时候它就是在处理非线性问题。那究竟什么时候选择哪一个核函数呢？

可以观察到，

• 线性核函数和多项式核函数在非线性数据上表现会浮动，如果数据相对线性可分，则表现不错，如果是像环形数据那样彻底不可分的，则表现糟糕。在线性数据集上，线性核函数和多项式核函数即便有扰动项也可以表现不错，可见多项式核函数是虽然也可以处理非线性情况，但更偏向于线性的功能。
• Sigmoid核函数就比较尴尬了，它在非线性数据上强于两个线性核函数，但效果明显不如rbf，它在线性数据上完全 比不上线性的核函数们，对扰动项的抵抗也比较弱，所以它功能比较弱小，很少被用到。
• rbf，高斯径向基核函数基本在任何数据集上都表现不错，属于比较万能的核函数。我个人的经验是，无论如何先 试试看高斯径向基核函数，它适用于核转换到很高的空间的情况，在各种情况下往往效果都很不错，如果rbf效果不好，那我们再试试看其他的核函数。另外，多项式核函数多被用于图像处理之中。

举个例子：用SVM实现二分类（硬间隔）

数据集来自：乳腺癌数据集，569个样本，30个特征

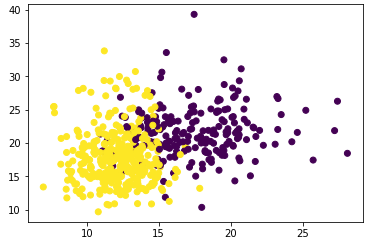
from sklearn.datasets import load_breast_cancer from sklearn.svm import SVC from sklearn.model_selection import train_test_split import matplotlib.pyplot as plt from time import time import datetime import numpy as np data = load_breast_cancer() X = data.data y = data.target plt.scatter(X[:,0],X[:,1],c=y) plt.show()
matplotlib.pyplot.scatter(x, y, s=None, c=None, marker=None, cmap=None, norm=None, vmin=None, vmax=None, alpha=None, linewidths=None, verts=None, edgecolors=None,*, data=None, **kwargs) x,y：表示的是大小为(n,)的数组，也就是我们即将绘制散点图的数据点 s:是一个实数或者是一个数组大小为(n,)，这个是一个可选的参数。 c:表示的是颜色，也是一个可选项。默认是蓝色'b',表示的是标记的颜色，或者可以是一个表示颜色的字符，或者是一个长度为n的表示颜色的序列等等，但是c不可以是一个单独的RGB数字，也不可以是一个RGBA的序列。可以是他们的2维数组（只有一行）。 marker:表示的是标记的样式，默认的是'o'。 cmap:Colormap实体或者是一个colormap的名字，cmap仅仅当c是一个浮点数数组的时候才使用。如果没有申明就是image.cmap norm:Normalize实体来将数据亮度转化到0-1之间，也是只有c是一个浮点数的数组的时候才使用。如果没有申明，就是默认为colors.Normalize。 vmin,vmax:实数，当norm存在的时候忽略。用来进行亮度数据的归一化。 alpha：实数，0-1之间。 linewidths:也就是标记点的长度。
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=420)
train_test_split函数用于将矩阵随机划分为训练子集和测试子集，并返回划分好的训练集测试集样本和训练集测试集标签。 格式：X_train,X_test, y_train, y_test =cross_validation.train_test_split(train_data,train_target,test_size=0.3, random_state=0) 参数解释： train_data：被划分的样本特征集 train_target：被划分的样本标签 test_size：如果是浮点数，在0-1之间，表示样本占比；如果是整数的话就是样本的数量 random_state：是随机数的种子。 随机数种子：其实就是该组随机数的编号，在需要重复试验的时候，保证得到一组一样的随机数。比如你每次都填1，其他参数一样的情况下你得到的随机数组是一样的。但填0或不填，每次都会不一样。随机数的产生取决于种子，随机数和种子之间的关系遵从以下两个规则：种子不同，产生不同的随机数；种子相同，即使实例不同也产生相同的随机数。
Kernel = ['linear','poly','rbf','sigmoid'] for kernel in Kernel: start_time = time() clf = SVC(kernel = kernel, gamma = 'auto', degree = 1, cache_size = 5000, ).fit(X_train,y_train) print('kernel=%s,准确率=%f'%(kernel,clf.score(X_test,y_test))) print('用时',(time()-start_time))
首先，乳腺癌数据集是一个线性数据集，线性核函数跑出来的效果很好。rbf和sigmoid两个擅长非线性的数据从效果上来看完全不可用。其次，线性核函数的运行速度远远不如非线性的两个核函数
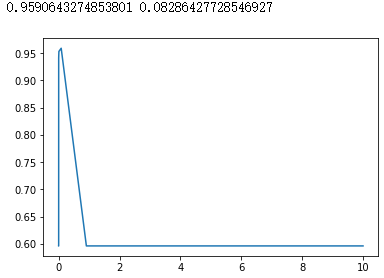
rbf核 score = [] gamma_range = np.logspace(-50, 1, 50) #返回在对数刻度上均匀间隔的数字 for i in gamma_range: clf = SVC(kernel="rbf",gamma = i,cache_size=5000).fit(X_train,y_train) score.append(clf.score(X_test,y_test)) print(max(score),gamma_range[score.index(max(score))]) plt.plot(gamma_range,score) plt.show()
但对于多项式核函数来说，一切就没有那么容易了，因为三个参数共同作用在一个数学公式上影响它的效果，因此我们往往使用网格搜索来共同调整三个对多项式核函数有影响的参数。 多项式核 from sklearn.model_selection import StratifiedShuffleSplit from sklearn.model_selection import GridSearchCV time0 = time() gamma_range = np.logspace(-10,1,20) coef0_range = np.linspace(0,5,10) param_grid = dict(gamma = gamma_range,coef0 = coef0_range) cv = StratifiedShuffleSplit(n_splits=5, test_size=0.3, random_state=420) grid = GridSearchCV(SVC(kernel = "poly",degree=1,cache_size=5000),param_grid=param_grid, cv=cv) grid.fit(X, y) print("The best parameters are %s with a score of %0.5f" %(grid.best_params_, grid.best_score_))
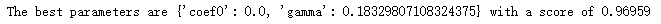可以发现，网格搜索为我们返回了参数coef0=0，gamma=0.18329807108324375，但整体的分数是0.96959， 虽然比调参前略有提高， 但依然没有超过线性核函数核rbf的结果。可见，如果最初选择核函数的时候，你就发现多项式的结果不如rbf和线性核函数,那就不要挣扎了, 试试看调整rbf或者直接使用线性

  

　　但从核函数的公式来看，我们其实很难去界定具体每个参数如何影响了SVM的表现。当gamma的符号变化，或者 degree的大小变化时，核函数本身甚至都不是永远单调的。所以如果我们想要彻底地理解这三个参数，我们要先推 导出它们如何影响核函数地变化，再找出核函数的变化如何影响了我们的预测函数（可能改变我们的核变化所在的 维度），再判断出决策边界随着预测函数的改变发生了怎样的变化。无论是从数学的角度来说还是从实践的角度来 说，这个过程太复杂也太低效。所以，我们往往避免去真正探究这些参数如何影响了我们的核函数，而直接使用学 习曲线或者网格搜索来帮助我们查找最佳的参数组合。对于高斯径向基核函数，调整gamma的方式其实比较容易，那就是画学习曲线。

软间隔与重要参数C

 

 

 

 

 

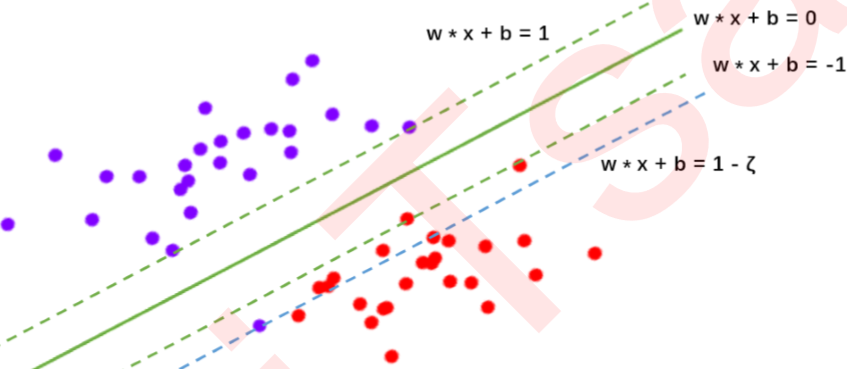
　　可能存在着一条直线能够将大部分数据点的类别划分正确，但无论如何也无法将全部的点分对，如同下图所展示的图，存在着混杂在红色类中的紫色点，这种情况下没有一条直线能够将两类数据完全分类正确。这个时候，我们的决策边界就不是单纯地寻求最大边际了，因为对于软间隔地数据来说，边际越大被分错的样本也就会越多，因此我们需要找出一个”最大边际“与”被分错的样本数量“之间的平衡。参数C用于权衡”训练样本的正确 分类“与”决策函数的边际最大化“两个不可同时完成的目标，希望找出一个平衡点来让模型的效果最佳。

 　　

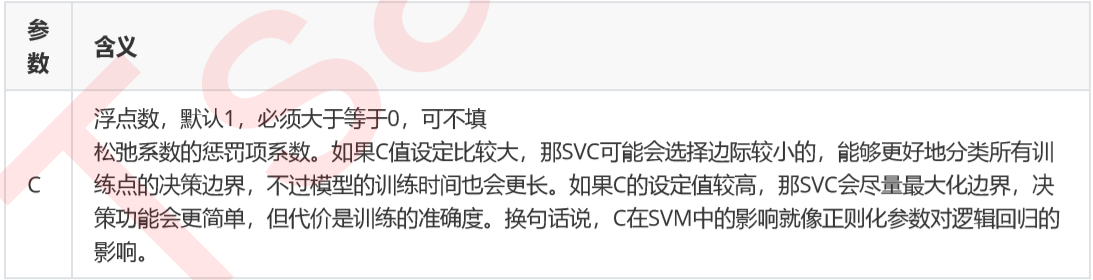
　　在实际使用中，C和核函数的相关参数（gamma，degree等等）们搭配，往往是SVM调参的重点。与gamma不同，C没有在对偶函数中出现，并且是明确了调参目标的，所以我们可以明确我们究竟是否需要训练集上的高精确度来调整C的方向。默认情况下C为1，通常来说这都是一个合理的参数。如果我们的数据很嘈杂，那我们往往减小 C。当然，我们也可以使用网格搜索或者学习曲线来调整C的值。

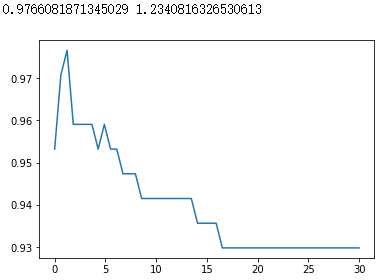
score = [] C_range = np.linspace(0.01,30,50) for i in C_range: clf = SVC(kernel="linear",C=i,cache_size=5000).fit(X_train,y_train) score.append(clf.score(X_test,y_test)) print(max(score), C_range[score.index(max(score))]) plt.plot(C_range,score) plt.show()
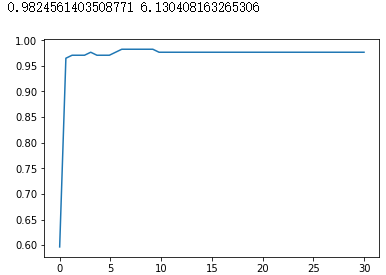
#换rbf score = [] C_range = np.linspace(0.01,30,50) for i in C_range: clf = SVC(kernel="rbf",C=i,gamma = 0.012742749857031322,cache_size=5000).fit(X_train,y_train) score.append(clf.score(X_test,y_test)) print(max(score), C_range[score.index(max(score))]) plt.plot(C_range,score) plt.show()
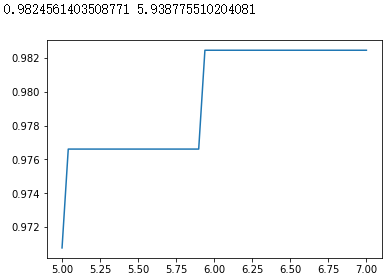
#进一步细化 score = [] C_range = np.linspace(5,7,50) for i in C_range: clf = SVC(kernel="rbf",C=i,gamma = 0.012742749857031322,cache_size=5000).fit(X_train,y_train) score.append(clf.score(X_test,y_test)) print(max(score), C_range[score.index(max(score))]) plt.plot(C_range,score) plt.show()
此时，我们找到了乳腺癌数据集上的最优解：rbf核函数下的98.24%的准确率。 当然，我们还可以使用交叉验证来改进我们的模型，获得不同测试集和训练集上的交叉验证结果。

二、用SVM实现多分类

1.直接法：

　　直接在目标函数上进行修改，将多个分类面的参数求解合并到一个最优化问题中，通过求解该最优化问题“一次性”实现多分类。但这种计算复杂度比较高，实现起来比较困难，只适合用于小型问题中；

2.间接法：

　　主要是通过组合多个二分类器来实现多分类器的构造，常见的方法有one-against-one和one-against-all两种。

（1）一对多法（one-versus-rest,简称OVR SVMs）

训练时依次把某个类别的样本归为一类，其他剩余的样本归为另一类，这样k个类别的样本就构造出了k个SVM

假如我有四类要划分（也就是4个label），A、B、C、D

于是我在抽取训练集的时候，分别抽取

　　（1）A所对应的向量作为正集，B，C，D所对应的向量作为负集；

　　（2）B所对应的向量作为正集，A，C，D所对应的向量作为负集；

　　（3）C所对应的向量作为正集，A，B，D所对应的向量作为负集；

　　（4）D所对应的向量作为正集，A，B，C所对应的向量作为负集；

　　　　　　　　

使用这四个训练集分别进行训练，然后的得到四个训练结果文件。在测试的时候，把对应的测试向量分别利用这四个训练结果文件进行测试。最后每个测试都有一个结果f1(x),f2(x),f3(x),f4(x)。于是最终的结果便是这四个值中最大的一个作为分类结果。

优点：训练k个分类器，个数较少，其分类速度相对较快。

缺点：

• 每个分类器的训练都是将全部的样本作为训练样本，这样在求解二次规划问题时，训练速度会随着训练样本的数量的增加而急剧减慢；
• 同时由于负类样本的数据要远远大于正类样本的数据，从而出现了样本不对称的情况，且这种情况随着训练数据的增加而趋向严重。解决不对称的问题可以引入不同的惩罚因子，对样本点来说较少的正类采用较大的惩罚因子C。
• 还有就是当有新的类别加进来时，需要对所有的模型进行重新训练。

（2）一对一法（one-versus-one，简称OVO SVMs或者pairwise）

其做法是在任意两类样本之间设计一个SVM，因此k个类别的样本就需要设计k(k-1)/2个SVM。

当对一个未知样本进行分类时，最后得票最多的类别即为该未知样本的类别。

 

假设有四类A,B,C,D四类。在训练的时候我选择A,B; A,C; A,D; B,C; B,D;C,D所对应的向量作为训练集，然后得到六个训练结果，在测试的时候，把对应的向量分别对六个结果进行测试，然后采取投票形式，最后得到一组结果。

　　投票是这样的：
　　A=B=C=D=0;
　　(A,B)-classifier 如果是A win,则A=A+1;otherwise,B=B+1;
　　(A,C)-classifier 如果是A win,则A=A+1;otherwise, C=C+1;
　　...
　　(C,D)-classifier 如果是A win,则C=C+1;otherwise,D=D+1;
　　The decision is the Max(A,B,C,D)

评价：这种方法虽然好,但是当类别很多的时候,model的个数是n*(n-1)/2,代价还是相当大的。

优点：不需要重新训练所有的SVM，只需要重新训练和增加语音样本相关的分类器。在训练单个模型时，相对速度较快。

缺点：所需构造和测试的二值分类器的数量关于k成二次函数增长，总训练时间和测试时间相对较慢。

 

直接方法尽管看起来简洁，但是在最优化问题求解过程中的变量远远多于第一类方法，训练速度不及间接方法，而且在分类精度上也不占优。当训练样本数非常大时，这一问题更加突出。正因如此，间接方法更为常用。

 

 

参考资料：

【1】SVM多分类的两种方式