R语言解读多元线性回归模型

转载：http://blog.fens.me/r-multi-linear-regression/

前言

本文接上一篇R语言解读一元线性回归模型。在许多生活和工作的实际问题中，影响因变量的因素可能不止一个，比如对于知识水平越高的人，收入水平也越高，这样的一个结论。这其中可能包括了因为更好的家庭条件，所以有了更好的教育；因为在一线城市发展，所以有了更好的工作机会；所处的行业赶上了大的经济上行周期等。要想解读这些规律，是复杂的、多维度的，多元回归分析方法更适合解读生活的规律。

由于本文为非统计的专业文章，所以当出现与教课书不符的描述，请以教课书为准。本文力求用简化的语言，来介绍多元线性回归的知识，同时配合R语言的实现。

目录

1. 多元线性回归介绍
2. 元线性回归建模
3. 模型优化
4. 案例：黑色系期货日K线数据验证

1. 多元线性回归介绍

对比一元线性回归，多元线性回归是用来确定2个或2个以上变量间关系的统计分析方法。多元线性回归的基本的分析方法与一元线性回归方法是类似的，我们首先需要对选取多元数据集并定义数学模型，然后进行参数估计，对估计出来的参数进行显著性检验，残差分析，异常点检测，最后确定回归方程进行模型预测。

由于多元回归方程有多个自变量，区别于一元回归方程，有一项很重要的操作就是自变量的优化，挑选出相关性最显著的自变量，同时去除不显著的自变量。在R语言中，有很方便地用于优化函数，可以很好的帮助我们来改进回归模型。

下面就开始多元线性回归的建模过程。

2. 多元线性回归建模

做过商品期货研究的人，都知道黑色系品种是具有产业链上下游的关系。铁矿石是炼钢的原材料，焦煤和焦炭是炼钢的能源资源，热卷即热轧卷板是以板坯为原料经加热后制成的钢板，螺纹钢是表面带肋的钢筋。

由于有产业链的关系，假设我们想要预测螺纹钢的价格，那么影响螺纹钢价格的因素可以会涉及到原材料，能源资源和同类材料等。比如，铁矿石价格如果上涨，螺纹钢就应该要涨价了。

2.1 数据集和数学模型

先从数据开始介绍，这次的数据集，我选择的期货黑色系的品种的商品期货，包括了大连期货交易所的 焦煤(JM)，焦炭(J)，铁矿石(I)，上海期货交易所的 螺纹钢(RU) 和 热卷(HC)。

数据集为2016年3月15日，当日白天开盘的交易数据，为黑色系的5个期货合约的分钟线的价格数据。

# 数据集已存在df变量中
> head(df,20)
                       x1    x2    x3   x4    y
2016-03-15 09:01:00 754.5 616.5 426.5 2215 2055
2016-03-15 09:02:00 752.5 614.5 423.5 2206 2048
2016-03-15 09:03:00 753.0 614.0 423.0 2199 2044
2016-03-15 09:04:00 752.5 613.0 422.5 2197 2040
2016-03-15 09:05:00 753.0 615.5 424.0 2198 2043
2016-03-15 09:06:00 752.5 614.5 422.0 2195 2040
2016-03-15 09:07:00 752.0 614.0 421.5 2193 2036
2016-03-15 09:08:00 753.0 615.0 422.5 2197 2043
2016-03-15 09:09:00 754.0 615.5 422.5 2197 2041
2016-03-15 09:10:00 754.5 615.5 423.0 2200 2044
2016-03-15 09:11:00 757.0 616.5 423.0 2201 2045
2016-03-15 09:12:00 756.0 615.5 423.0 2200 2044
2016-03-15 09:13:00 755.5 615.0 423.0 2197 2042
2016-03-15 09:14:00 755.5 615.0 423.0 2196 2042
2016-03-15 09:15:00 756.0 616.0 423.5 2200 2045
2016-03-15 09:16:00 757.5 616.0 424.0 2205 2052
2016-03-15 09:17:00 758.5 618.0 424.0 2204 2051
2016-03-15 09:18:00 759.5 618.5 424.0 2205 2053
2016-03-15 09:19:00 759.5 617.5 424.5 2206 2053
2016-03-15 09:20:00 758.5 617.5 423.5 2201 2050

数据集包括有6列:

• 索引, 为时间
• x1, 为焦炭(j1605)合约的1分钟线的报价数据
• x2, 为焦煤(jm1605)合约的1分钟线的报价数据
• x3, 为铁矿石(i1605)合约的1分钟线的报价数据
• x4, 为热卷(hc1605)合约的1分钟线的报价数据
• y, 为螺纹钢(rb1605)合约的1分钟线的报价数据

假设螺纹钢的价格与其他4个商品的价格有线性关系，那么我们建立以螺纹钢为因变量，以焦煤、焦炭、铁矿石和热卷的为自变量的多元线性回归模型。用公式表示为：

y = a + b * x1 + c * x2 + d * x3 + e * x4 + ε

• y，为因变量，螺纹钢
• x1，为自变量，焦煤
• x2，为自变量，焦炭
• x3，为自变量，铁矿石
• x4，为自变量，热卷
• a，为截距
• b,c,d,e，为自变量系数
• ε, 为残差，是其他一切不确定因素影响的总和，其值不可观测。假定ε服从正态分布N(0,σ^2)。

通过对多元线性回归模型的数学定义，接下来让我们利用数据集做多元回归模型的参数估计。

2.2. 回归参数估计

上面公式中，回归参数 a, b, c, d,e都是我们不知道的，参数估计就是通过数据来估计出这些参数，从而确定自变量和因变量之前的关系。我们的目标是要计算出一条直线，使直线上每个点的Y值和实际数据的Y值之差的平方和最小，即（Y1实际-Y1预测）^2+（Y2实际-Y2预测）^2+ …… +（Yn实际-Yn预测）^2 的值最小。参数估计时，我们只考虑Y随X自变量的线性变化的部分，而残差ε是不可观测的，参数估计法并不需要考虑残差。

类似于一元线性回归，我们用R语言来实现对数据的回归模型的参数估计，用lm()函数来实现多元线性回归的建模过程。

# 建立多元线性回归模型
> lm1<-lm(y~x1+x2+x3+x4,data=df)

# 打印参数估计的结果
> lm1

Call:
lm(formula = y ~ x1 + x2 + x3 + x4, data = df)

Coefficients:
(Intercept)           x1           x2           x3           x4  
   212.8780       0.8542       0.6672      -0.6674       0.4821  

这样我们就得到了y和x关系的方程。

y = 212.8780 + 0.8542 * x1 + 0.6672 * x2 - 0.6674 * x3 + 0.4821 * x4

2.3. 回归方程的显著性检验

参考一元线性回归的显著性检验，多元线性回归的显著性检验，同样是需要经过 T检验，F检验，和R^2(R平方)相关系统检验。在R语言中这三种检验的方法都已被实现，我们只需要把结果解读，我们可以summary()函数来提取模型的计算结果。

> summary(lm1)

Call:
lm(formula = y ~ x1 + x2 + x3 + x4, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.9648 -1.3241 -0.0319  1.2403  5.4194 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 212.87796   58.26788   3.653 0.000323 ***
x1            0.85423    0.10958   7.795 2.50e-13 ***
x2            0.66724    0.12938   5.157 5.57e-07 ***
x3           -0.66741    0.15421  -4.328 2.28e-05 ***
x4            0.48214    0.01959  24.609  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.028 on 221 degrees of freedom
Multiple R-squared:  0.9725,	Adjusted R-squared:  0.972 
F-statistic:  1956 on 4 and 221 DF,  p-value: < 2.2e-16

• T检验：所自变量都是非常显著***
• F检验：同样是非常显著，p-value < 2.2e-16
• 调整后的R^2：相关性非常强为0.972

最后，我们通过的回归参数的检验与回归方程的检验，得到最后多元线性回归方程为：

y = 212.87796 + 0.85423 * x1 + 0.66724 * x2 - 0.66741 * x3 + 0.48214 * x4

即

螺纹钢 = 212.87796 + 0.85423 * 焦炭 + 0.66724 * 焦煤 - 0.66741 * 铁矿石 + 0.48214 * 热卷

2.4 残差分析和异常点检测

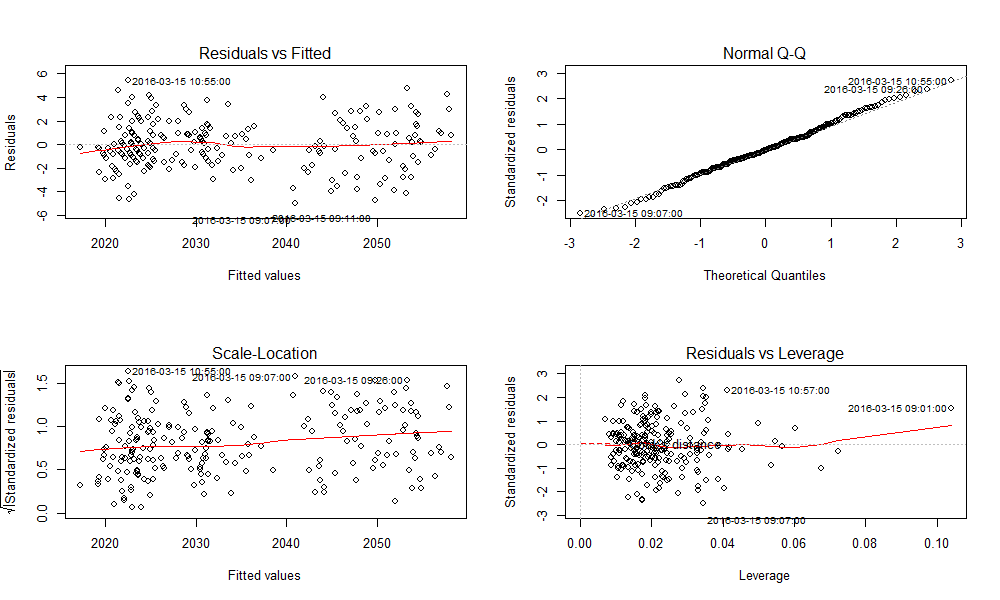
在得到的回归模型进行显著性检验后，还要在做残差分析(预测值和实际值之间的差)，检验模型的正确性，残差必须服从正态分布N(0,σ^2)。直接用plot()函数生成4种用于模型诊断的图形，进行直观地分析。

> par(mfrow=c(2,2))
> plot(lm1)

• 残差和拟合值(左上)，残差和拟合值之间数据点均匀分布在y=0两侧，呈现出随机的分布，红色线呈现出一条平稳的曲线并没有明显的形状特征。
• 残差QQ图(右上)，数据点按对角直线排列，趋于一条直线，并被对角直接穿过，直观上符合正态分布。
• 标准化残差平方根和拟合值(左下)，数据点均匀分布在y=0两侧，呈现出随机的分布，红色线呈现出一条平稳的曲线并没有明显的形状特征。
• 标准化残差和杠杆值(右下)，没有出现红色的等高线，则说明数据中没有特别影响回归结果的异常点。

结论，没有明显的异常点，残差符合假设条件。

2.5. 模型预测

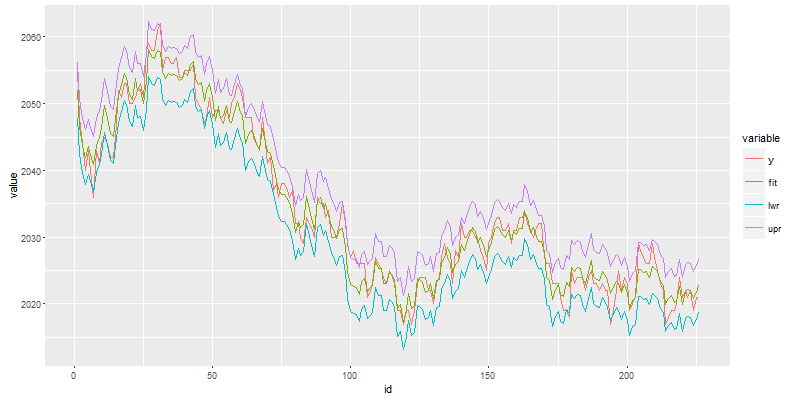
我们得到了多元线性回归方程的公式，就可以对数据进行预测了。我们可以用R语言的predict()函数来计算预测值y0和相应的预测区间，并把实际值和预测值一起可视化化展示。

> par(mfrow=c(1,1))  #设置画面布局

# 预测计算
> dfp<-predict(lm1,interval="prediction")

# 打印预测时
> head(dfp,10)
                fit      lwr      upr
2014-03-21 3160.526 3046.425 3274.626
2014-03-24 3193.253 3078.868 3307.637
2014-03-25 3240.389 3126.171 3354.607
2014-03-26 3228.565 3114.420 3342.710
2014-03-27 3222.528 3108.342 3336.713
2014-03-28 3262.399 3148.132 3376.666
2014-03-31 3291.996 3177.648 3406.344
2014-04-01 3305.870 3191.447 3420.294
2014-04-02 3275.370 3161.018 3389.723
2014-04-03 3297.358 3182.960 3411.755

# 合并数据
> mdf<-merge(df$y,dfp)	 

# 画图
> draw(mdf)

图例说明

• y, 实际价格，红色线
• fit, 预测价格，绿色线
• lwr，预测最低价，蓝色线
• upr，预测最高价，紫色线

从图中看出，实际价格y和预测价格fit，在大多数的时候都是很贴近的。我们的一个模型就训练好了！

3. 模型优化

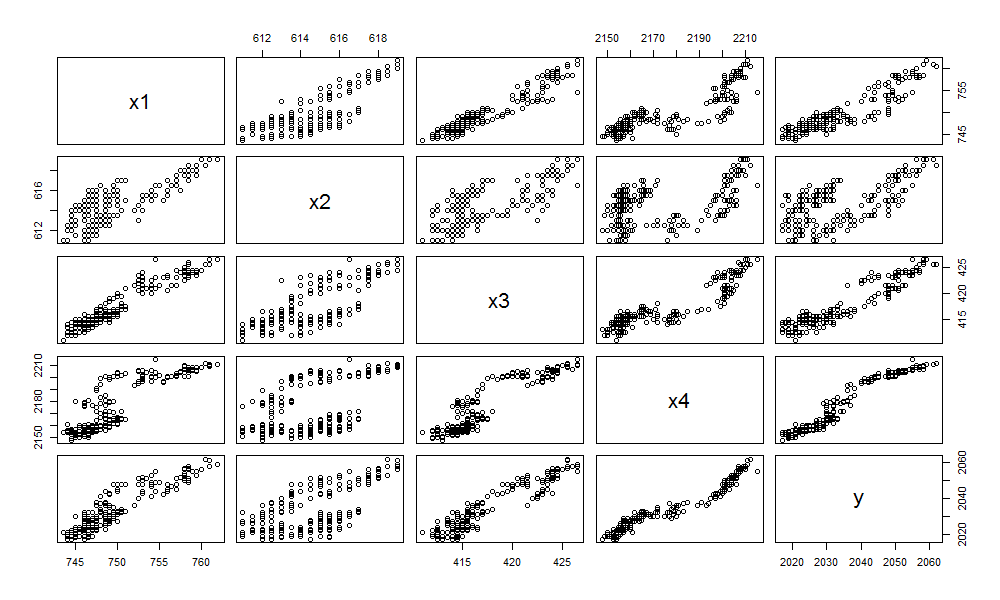
上文中，我们已经很顺利的发现了一个非常不错的模型。如果要进行模型优化，可以用R语言中update()函数进行模型的调整。我们首先检查一下每个自变量x1,x2,x3,x4和因变量y之间的关系。

pairs(as.data.frame(df))

从图中，我们可以发现x2与Y的关系，可能是最偏离线性的。那么，我们尝试对多元线性回归模型进行调整，从原模型中去掉x2变量。

# 模型调整
> lm2<-update(lm1, .~. -x2)

> summary(lm2)

Call:
lm(formula = y ~ x1 + x3 + x4, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-6.0039 -1.3842  0.0177  1.3513  4.8028 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 462.47104   34.26636   13.50  < 2e-16 ***
x1            1.08728    0.10543   10.31  < 2e-16 ***
x3           -0.40788    0.15394   -2.65  0.00864 ** 
x4            0.42582    0.01718   24.79  < 2e-16 ***
---
Signif. codes:  
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.142 on 222 degrees of freedom
Multiple R-squared:  0.9692,	Adjusted R-squared:  0.9688 
F-statistic:  2330 on 3 and 222 DF,  p-value: < 2.2e-16

当把自变量x2去掉后，自变量x3的T检验反而变大了，同时Adjusted R-squared变小了，所以我们这次调整是有问题的。

如果通过生产和原材料的内在逻辑分析，焦煤与焦炭属于上下游关系。焦煤是生产焦炭的一种原材料，焦炭是焦煤与其他炼焦煤经过配煤焦化形成的产品，一般生产 1 吨焦炭需要1.33 吨炼焦煤，其中焦煤至少占 30% 。

我们把焦煤 和 焦炭的关系改变一下，增加x1*x2的关系匹配到模型，看看效果。

# 模型调整
> lm3<-update(lm1, .~. + x1*x2)
> summary(lm3)

Call:
lm(formula = y ~ x1 + x2 + x3 + x4 + x1:x2, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.8110 -1.3501 -0.0595  1.2019  5.3884 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) 7160.32231 7814.50048   0.916    0.361    
x1            -8.45530   10.47167  -0.807    0.420    
x2           -10.58406   12.65579  -0.836    0.404    
x3            -0.64344    0.15662  -4.108 5.63e-05 ***
x4             0.48363    0.01967  24.584  < 2e-16 ***
x1:x2          0.01505    0.01693   0.889    0.375    
---
Signif. codes:  
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.029 on 220 degrees of freedom
Multiple R-squared:  0.9726,	Adjusted R-squared:  0.972 
F-statistic:  1563 on 5 and 220 DF,  p-value: < 2.2e-16

从结果中发现，增加了x1*x2列后，原来的x1,x2和Intercept的T检验都不显著。继续调整模型，从模型中去掉x1,x2两个自变量。

# 模型调整
> lm4<-update(lm3, .~. -x1-x2)
> summary(lm4)

Call:
lm(formula = y ~ x3 + x4 + x1:x2, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.9027 -1.2516 -0.0167  1.2748  5.8683 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  6.950e+02  1.609e+01  43.183  < 2e-16 ***
x3          -6.284e-01  1.530e-01  -4.108 5.61e-05 ***
x4           4.959e-01  1.785e-02  27.783  < 2e-16 ***
x1:x2        1.133e-03  9.524e-05  11.897  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.035 on 222 degrees of freedom
Multiple R-squared:  0.9722,	Adjusted R-squared:  0.9718 
F-statistic:  2588 on 3 and 222 DF,  p-value: < 2.2e-16

从调整后的结果来看，效果还不错。不过，也并没有比最初的模型有所提高。

对于模型调整的过程，如果我们手动调整测试时，一般都会基于业务知识来操作。如果是按照数据指标来计算，我们可以用R语言中提供的逐步回归的优化方法，通过AIC指标来判断是否需要参数优化。

#对lm1模型做逐步回归
> step(lm1)
Start:  AIC=324.51
y ~ x1 + x2 + x3 + x4

       Df Sum of Sq    RSS    AIC
               908.8 324.51
- x3    1     77.03  985.9 340.90
- x2    1    109.37 1018.2 348.19
- x1    1    249.90 1158.8 377.41
- x4    1   2490.56 3399.4 620.65

Call:
lm(formula = y ~ x1 + x2 + x3 + x4, data = df)

Coefficients:
(Intercept)           x1           x2           x3           x4  
   212.8780       0.8542       0.6672      -0.6674       0.4821  

通过计算AIC指标，lm1的模型AIC最小时为324.51，每次去掉一个自变量都会让AIC的值变大，所以我们还是不调整比较好。

对刚才的lm3模型做逐步回归的模型调整。

#对lm3模型做逐步回归
> step(lm3)
Start:  AIC=325.7               #当前AIC
y ~ x1 + x2 + x3 + x4 + x1:x2

        Df Sum of Sq    RSS    AIC
- x1:x2  1      3.25  908.8 324.51
                905.6 325.70
- x3     1     69.47  975.1 340.41
- x4     1   2487.86 3393.5 622.25

Step:  AIC=324.51               #去掉x1*x2项的AIC
y ~ x1 + x2 + x3 + x4

       Df Sum of Sq    RSS    AIC
               908.8 324.51
- x3    1     77.03  985.9 340.90
- x2    1    109.37 1018.2 348.19
- x1    1    249.90 1158.8 377.41
- x4    1   2490.56 3399.4 620.65

Call:
lm(formula = y ~ x1 + x2 + x3 + x4, data = df)

Coefficients:
(Intercept)           x1           x2           x3           x4  
   212.8780       0.8542       0.6672      -0.6674       0.4821  

通过AIC的判断，去掉X1*X2项后AIC最小，最后的检验结果告诉我们，还是原初的模型是最好的。

4. 案例：黑色系期货日K线数据验证

最后，我们用上面5个期货合约的日K线数据测试一下，找到多元回归关系。

> lm9<-lm(y~x1+x2+x3+x4,data=df)  # 日K线数据
> summary(lm9)

Call:
lm(formula = y ~ x1 + x2 + x3 + x4, data = df)

Residuals:
     Min       1Q   Median       3Q      Max 
-173.338  -37.470    3.465   32.158  178.982 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 386.33482   31.07729  12.431  < 2e-16 ***
x1            0.75871    0.07554  10.045  < 2e-16 ***
x2           -0.62907    0.14715  -4.275 2.24e-05 ***
x3            1.16070    0.05224  22.219  < 2e-16 ***
x4            0.46461    0.02168  21.427  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 57.78 on 565 degrees of freedom
Multiple R-squared:  0.9844,	Adjusted R-squared:  0.9843 
F-statistic:  8906 on 4 and 565 DF,  p-value: < 2.2e-16

数据集的基本统计信息。

> summary(df)
     Index                           x1               x2       
 Min.   :2014-03-21 00:00:00   Min.   : 606.5   Min.   :494.0  
 1st Qu.:2014-10-21 06:00:00   1st Qu.: 803.5   1st Qu.:613.1  
 Median :2015-05-20 12:00:00   Median : 939.0   Median :705.8  
 Mean   :2015-05-21 08:02:31   Mean   : 936.1   Mean   :695.3  
 3rd Qu.:2015-12-16 18:00:00   3rd Qu.:1075.0   3rd Qu.:773.0  
 Max.   :2016-07-25 00:00:00   Max.   :1280.0   Max.   :898.0  

       x3              x4             y       
 Min.   :284.0   Min.   :1691   Min.   :1626  
 1st Qu.:374.1   1st Qu.:2084   1st Qu.:2012  
 Median :434.0   Median :2503   Median :2378  
 Mean   :476.5   Mean   :2545   Mean   :2395  
 3rd Qu.:545.8   3rd Qu.:2916   3rd Qu.:2592  
 Max.   :825.0   Max.   :3480   Max.   :3414  

对于日K线数据，黑色系的5个品种，同样具有非常强的相关关系，那么我们就可以把这个结论应用到实际的交易中了。