问题背景
假设有这样的一个需求：判断某一朵花是不是鸢尾花。我们知道不同品种的花，其长得是不一样，所以我们可以通过花的若干外观特征（花萼长度、花萼宽度、花瓣长度、花瓣宽度等）来表示这一朵花。
基于这个思路，我们采集N朵花并对其标注，得到以下的数据集。
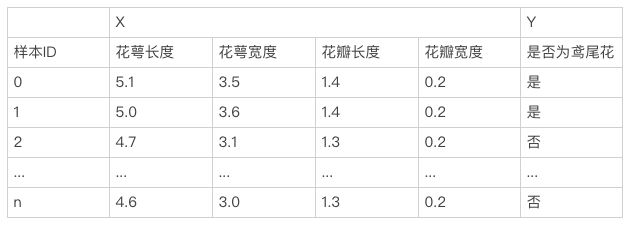
考虑最简单的一种情形，Y(是否为鸢尾花)，与特征X线性相关，W定义为相关系数，即模型F可以用下面公式表述：
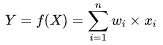
化简写成向量化形式：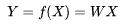
，也就是线性回归，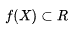
现在问题来了，是和否是两种状态，在计算机科学上我们常用1/0开关量来表述，但是从表示式的值域上看数学公式: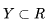 
能取任意值，这是没办法直接成表述0/1开关量。那如何解决这个问题呢？通过一个转换函数(又称为激活函数)，将线性回归转换逻辑回归。
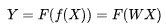
建模思路
并不是任意函数都可以作激活函数使用的，激活函数具有以下几种良好的性质：
非线性，线性函数的复合线性函数仍是线性函数，故线性激活函数不能带来非线性的变换，使用这样激活函数不能增强模型的表达能力，如此一来就没办法拟合复杂的实现问题了，所以激活函数必须非线性的。
连续可微，如果函数不可微分，就没办法通过梯度下降法来迭代优化，以得到近似的最优解了。如果激活函数不可微，可能需要其他各复杂的数学工具来求解，一是未必会有解，二是计算成本太高，难以实现和落地。
单调性，线性函数本身是单调，这个本身是一定的物理意义的，所以经过激活函数转换后也保持这个性质，不能改变其单调性。 满足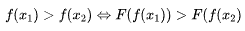
直接转换
通过一个分段函数，把f(x)直接映射成0或1，如公式所示：
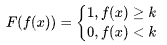
但是，这个分段函数不连续不可微不单调，还带一个额外的参数k，所以这种分段函数并不适合作激活函数使用。
间接映射
不直接映射成0或1，而是将f(x)的值域压缩到(0,1)之间，如公式所示：
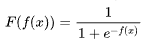
这就是sigmoid函数了，下图为sigmoid函数的图像。
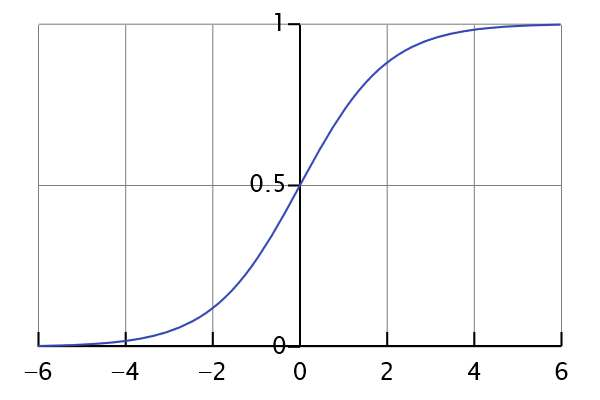
显然是这个函数是具有上面提到的激活函数的三种优良性质。同时将输出压缩到(0,1)区间上，有一个很直观感受是，我们可以把这个输出值理解为一种概率，在这个问题上指的是鸢尾花的概率，当这个概率值大于0.5，说明鸢尾花概率大即1，反之则不是鸢尾花即0，这就能实现分类的判别了。
实现逻辑
那既然现在有了sigmoid激活函数，我们该如何利用它训练模型呢？模型之所以能训练是依赖于两个神器:损失函数和梯度下降，前者能量化我们模型预测与真实结果的误差、确定优化的目标函数，后者能知道如何去减少误差、具体地优化目标函数。
损失函数
sigmoid激活函数输出值可以看作是概率，具体地我们可以把这个概率，看成是预测结果为是的概率。
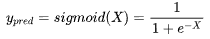
我们需要预测的分类结果要么为是要么为否，只有两种情况，显然样本X是服从伯努利(0-1)分布。假定样本X，当分类标签真值y为1时，我们就看y_pred也是sigmoid的输出值（模型预测为是的概率），0是1的互斥事件，当分类标签真值为0时，我们就看1-y_pred（模型预测为否的概率），所以条件概率P(Y|X)可以量化出模型预测的准确程度了。
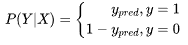
合并化简，整合成统一形式
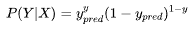
P(Y|X)就是模型预测结果，显然P(Y|X)的值越接近于1，说明模型预测结果越准。一个数据集有N个样本，每个样本之间独立的，所以在模型在整个数据上好坏，可以这样定义：
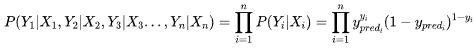
显然，要使得模型的效果最佳，则得找到一个最佳参数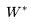
使得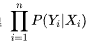
能取到最大值，这个就是最优化方法里面的极大使然估计(MLE)了，我们找到损失函数了。
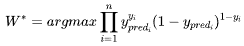
接下来，我们得看看如何转换这个损失函数：加负号（最大值问题转化最小值问题，梯度下降能找最小值），取对数（不改单调性，把复杂的连乘变成简单的连加）
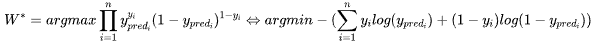
梯度下降
确定了目标函数之后，接下来就可以利用梯度下降，用迭代更新参数W，使其不断逼近目标函数的极值点。
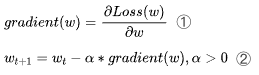
梯度推导：
联立式②③可见
由此可见，t+1时刻模型预测误差总会比在t时刻更小，通过这样迭代，模型就能不断学习和调整，一直到偏导数为0的(局部)最优极值点，这时候参数便无法再继续调整了，模型也就停止再训练了。
结语
逻辑回归(Logistic Regression)是机器学习上面一个最简单、最基础的模型框架和基本范式，不夸张地说它是机器学习奠基石之一，后续的机器学习模型，很多都是立足于这个基础的模型框架上，提出各种形式拓展与改进。
深刻地理解逻辑回归模型，梳理逻辑回归模型背后建模思路、因果缘由、实现逻辑，能让我们对机器学习的方法论有一个更全面更清晰的认知。