题外话
我很早就对人工智能是非常感兴趣的。记得我大学的毕业论文,就是使用遗传算法解决了一个经典的寻路问题。
我一直对人类经典的思想是非常敬畏和崇拜的,比如传统的计算机数据结构算法问题,例如经典的排序算法或者动态规划思想,把一些看似
复杂的问题竟然用短短十几行甚至一个 for 循环就能解决,这令我感受到了一种美学,也同时对人类的伟大思想而赞叹。
但传统的计算机算法其实还是通过,人来编写代码,人来通过完整的、解决问题的思路来解决问题。但如果机器能有自己的思想,如果它自己就能“学习”到解决问题的方法,岂不是非常 cool 的一件事。但以我目前的认知来看,现在的人工智能是更像是一种工具,一种“数学工具”,一种“统计学工具”,
它是从大量数据里总结出了一种“规律”,用来解决实际问题。它离电脑真正有思想还相距甚远,甚至以目前来看,二者可能并不是一回事。可能让机器具有思维,还需要在其他学科上进行突破比如人的认知机制,脑科学进行突破。哈哈扯远了。
先来介绍自己的一些简单认识。
线性
- 什么是线性?
有一类几何对象,比如直线、平面、立方体,看上去都是有棱有角的,都是“直”的,在数学中称为线性
要处理它们相关的问题就非常简单。比如在高中就学过,两根直线可以用两个线性方程来表示,想求它们交点的话:
联立出两者的方程组,求出该方程组的解就可以得到交点
- 为什么要研究线性
(1)我们所处的世界、宇宙太复杂了,很多现象都无法理解,更谈不上用数学去描述;
(2)有一些符合特定条件的复杂问题,可以转化为简单的线性问题。线性问题就可以完全被理解,完全可以被数学所描述
回归
以我目前的认知来看,机器学习主要的任务有两类。
第一就是分类任务,比如
- 判断一张图片里的是猫还是狗 (二分类,因为我定义目标结论有两种,即猫或者狗)
- 判断一个股票明天是涨还是跌
- 判断一个图片中的数字是几(多分类。因为我定义目标结论有 10 种,0 到 9)

也就是说,分类的结果是,人为预先定义的结果范围里的一种
而第二类任务就是回归任务,而它得出的结果是一个连续数字的值,而非类别。
例如
- 预测房屋价格
- 预测股票价格
什么是机器学习
这是我目前的浅显理解。机器学习目前我觉得是一种数学工具。通过喂给机器大量的学习资料,然后机器运行一个机器学习算法,训练出了一个模型。然后再向机器丢入问题,机器通过这个模型运算得出结果。
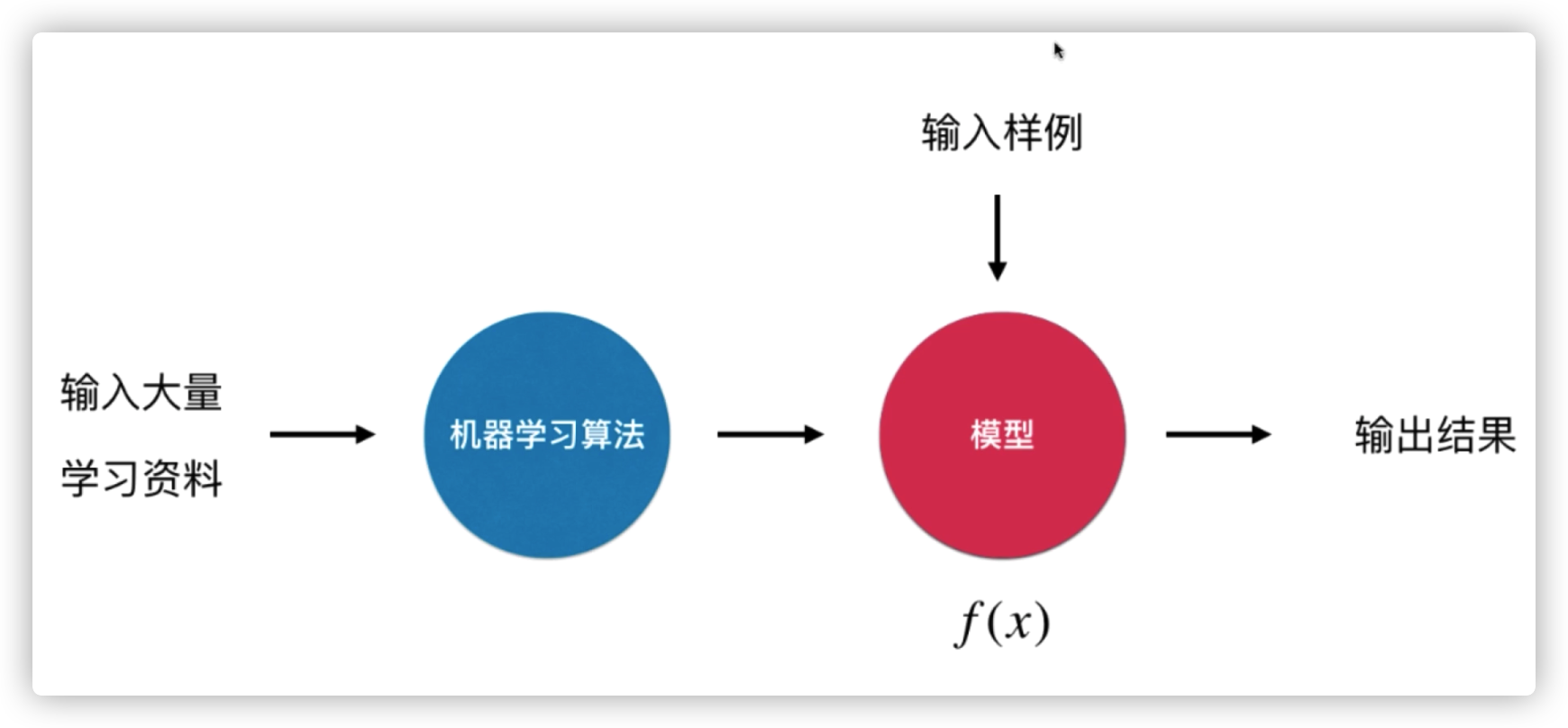
线性回归的初步感性理解
比如我收集到了有 x, y 的两组数据(比如年龄和身高),我想要知道这两组变量是否有线性关系。那么我先以一个变量为 x 轴,另一个变量为 y 轴画出这样一副散点图。
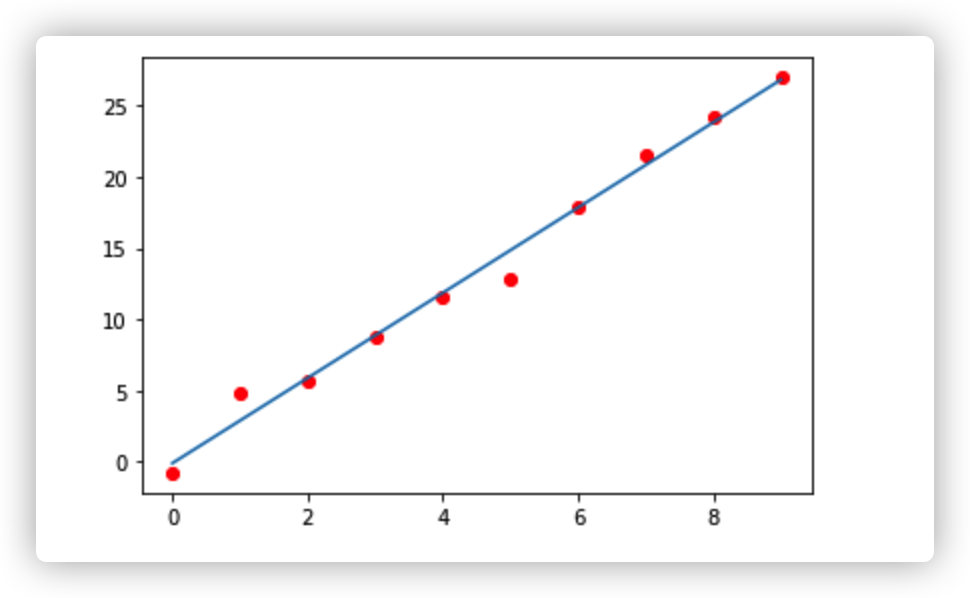
那么我就可以找出这样的一条直线。这条直线的特征是:尽可能的离所有离散点最近,也可以表述成,每个离散点离直线距离的差值之和最小。
那么我就可以很好的根据我算出的这条直线,由已知的 x 值,来预测的未知的 y 值。
假如说 x, y 有线性关系的话,那么预测的效果还是很不错的。所以线性回归的主要任务是,找出这条直线。
单变量线性回归
我们先从单变量线性回归开始理解,即假设 x 只有一个特征(比如一氧化氮浓度),y 是房价。
根据前文提到的感性理解,我们的目标就是找到最佳的直线方程:
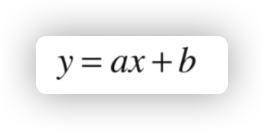
其实就是求参数 a 和 b 的过程。
那其实我们的目标就是,使得根据每一个 x 点,使得
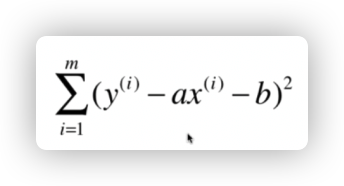
最小。这个方程叫做损失函数。
你可能想问为什么是差的平方和最小?而不是差的绝对值和最小或者差的 3 或者 4 次方最小?
差的平方和最小在数学中叫做最小二乘法,这里给出一个链接
https://www.zhihu.com/question/24095027,这里不再细究。
所以一类机器学习算法的基本思路是: 通过确定问题的损失函数,然后最优化损失函数,来获得机器学习的模型。
怎么求得这个损失函数的最小值,即求 a 和 b 的值。则需要对 a 和 b 分别进行求导。导数为 0 的点则为极值点。
现在我们对 a 进行求导(复合函数的链式求导法则):
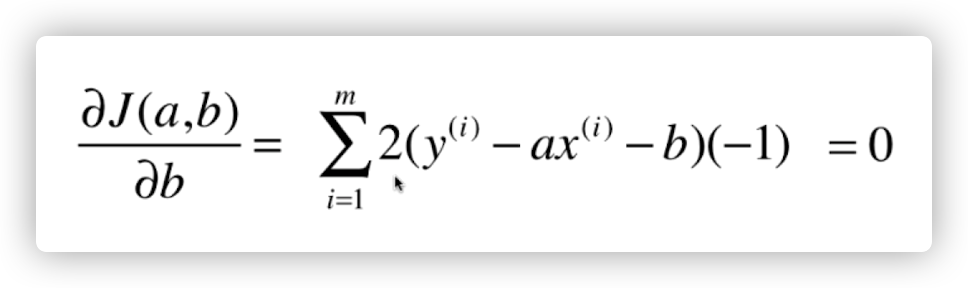
化简一下:

根据同样的过程得出 a,化简过程省略:
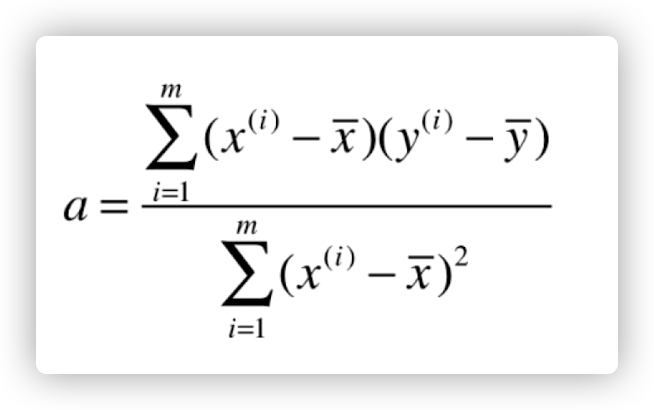
然后 python 实现一下:
简单来说我需要定义两个方法。
- fit 拟合方法。或者我们常说的训练方法。通过将训练数据作为参数传入这个方法,得出模型的各个参数。
- predict 预测方法。将 x 值带入这个方法,得出预测值
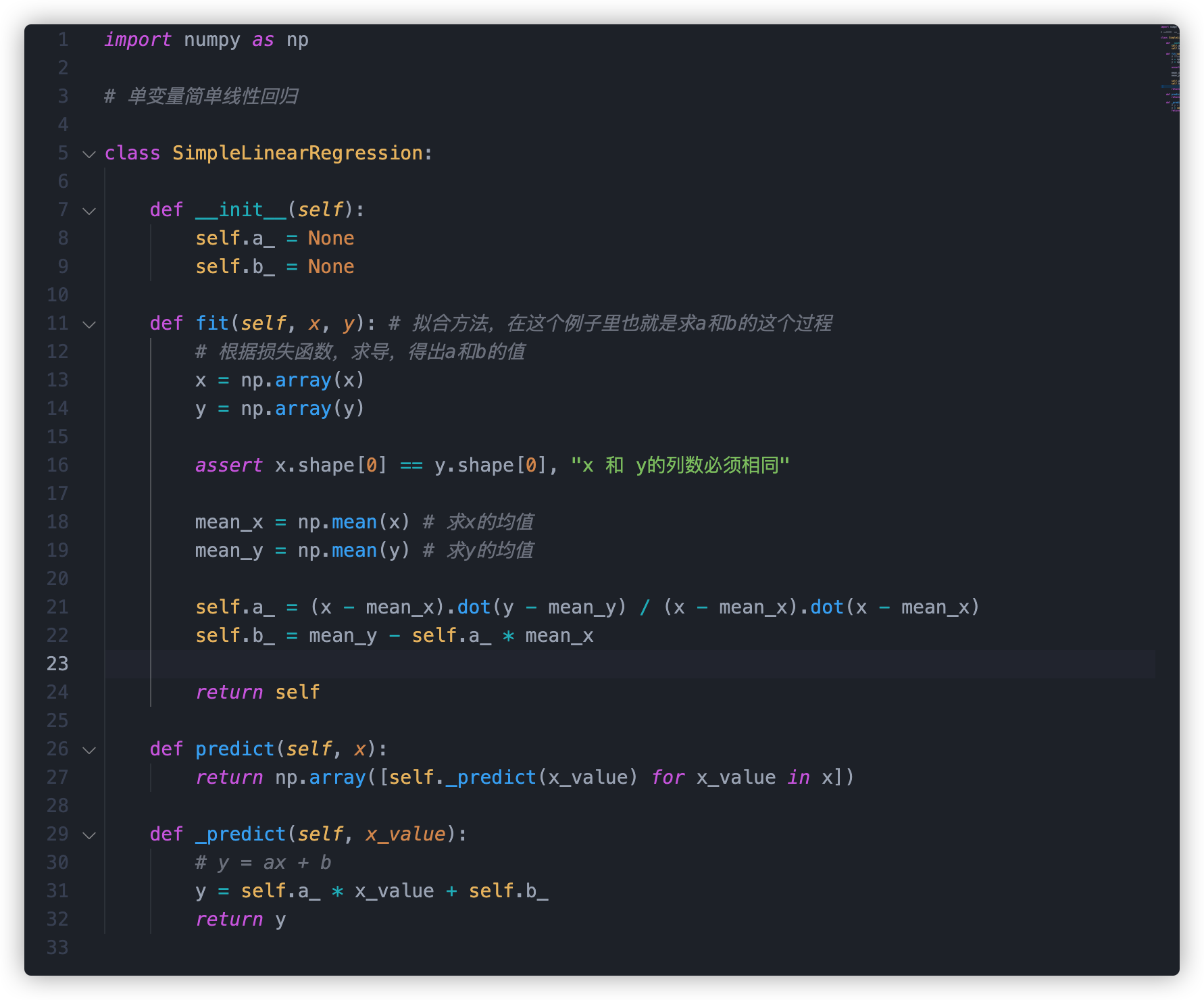
这里需要注意一下:这里采用了向量化代替了循环去求 a。 我们看到,a 的分子分母实际上用循环也可以求,
但是实际上,a 的分子分母其实可以看成向量的点乘(即向量 a 里的每一个分量乘以向量 b 里的每一个分量)。
这样做有两个好处:
- 代码更清晰
- 向量是并行运算。(调用 GPU 流处理器进行并行运算)远快于 cpu 里进行循环
当把这个 a 和 b 的参数求出之后,我们就得出了一个模型(在这个例子中是 y=ax+b),然后我们就可以进行预测了,把 x 带入这个方程中,就可以得出预测后的这个 y 值。
多元线性回归
理解了单变量线性回归之后,我们就开始需要解决,当特征为多个的时候,怎么进行预测?
也就是多元线性回归。
我们可以理解一下,多元线性回归实际要求的是这样的一个方程
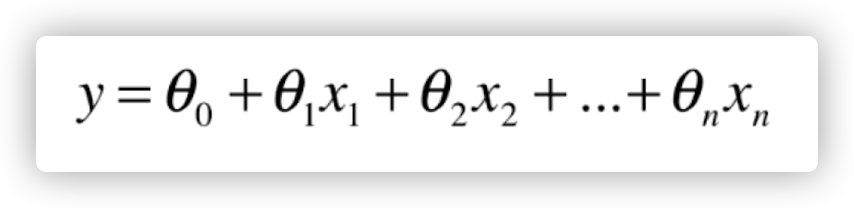
即每一个特征前面都有一个常数系数,再加一个常数(截距)。
这里我们把这些系数整理成一个(列)向量
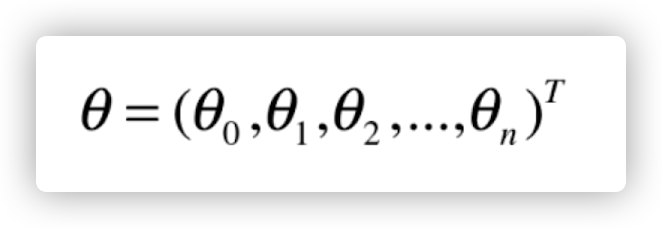
然后我们为了方便起见,设置一个 x0, x0 恒等于 1,那么我们最终就化简成了下面两个向量的点乘
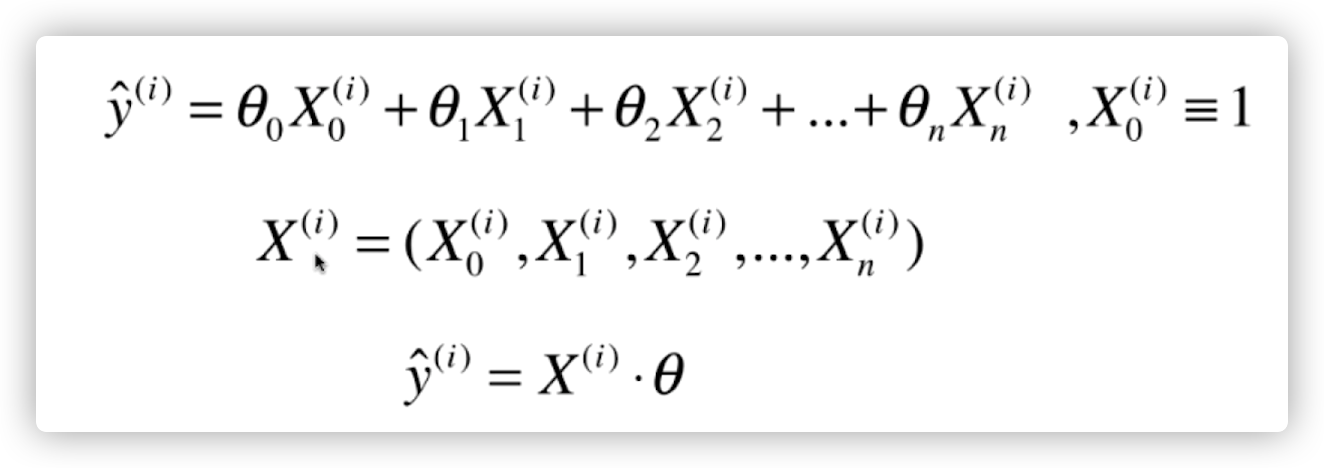
然后把所有的 x 向量(样本)组合成一个矩阵,将 theta 整理成一个列向量。那么 y(向量)就是所有 x 向量的预测值。这里用到了矩阵和向量的乘法(哈哈忘了的话得复习一下线性代数)。

那么根据最小二乘法,我们的目标就是使得 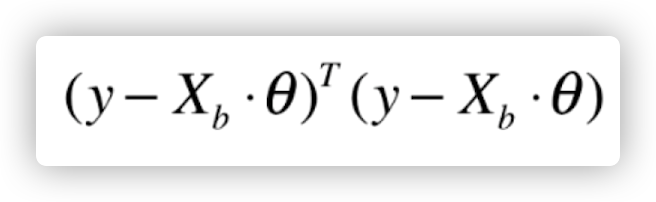
最小。也就是要对整个矩阵进行求导,具体推导过程省略,这里给出最终 theta 的解:
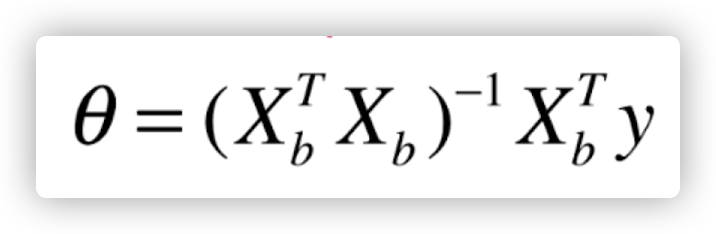
也就是我们通过数学推导,直接求出了参数的数学解,然而一般而言,能够直接得出参数数学解的机器学习方法还是比较少的,有可能还需要借助其他方法比如梯度下降才能够求出参数。
多元线性回归的实现
接下来根据这个数学解进行实现。
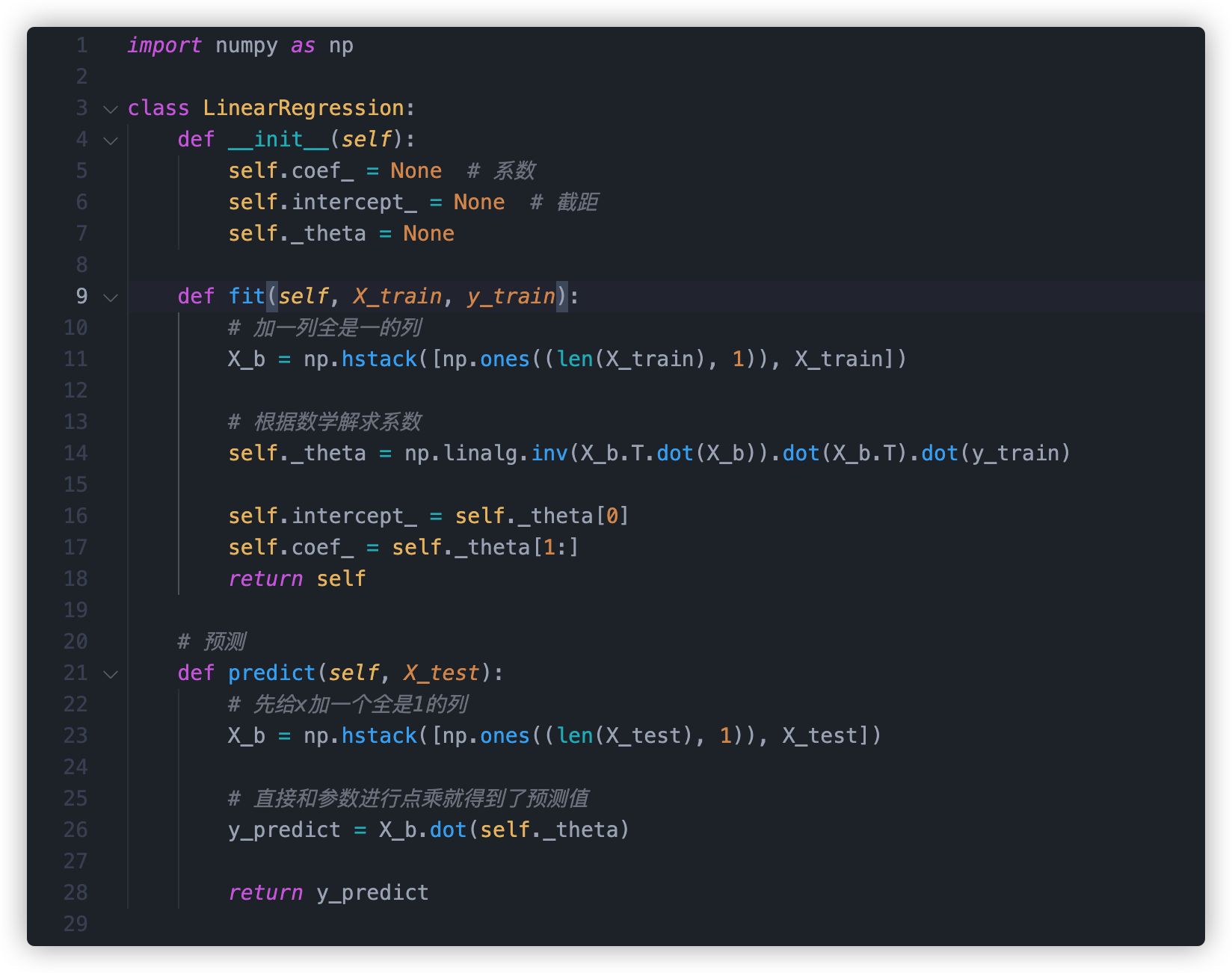
简单线性回归实战(波士顿房价预测)
这个波士顿房价数据集是 sklearn(一个机器学习框架)自带的数据集
其实我看到这个数据集时也懵了,这个例子是带我们预测房价吗?预测明天深圳的房价?
我觉得是可以这样理解,通过收集一些特征(学习资料)如下图和波士顿某些地区的平均房价(目标结论),来推测出你或者房地产商卖房子时应该怎么定价比较划算。或者说通过这个数据集来理解,哪个因素对于房价影响更大。
数据介绍
该数据集包含马萨诸塞州波士顿郊区的房屋信息数据,来自 UCI 机器学习知识库(数据集已下线),于 1978 年开始统计,包括 506 个样本,每个样本包括 12 个特征变量和该地区的平均房价。
字段含义
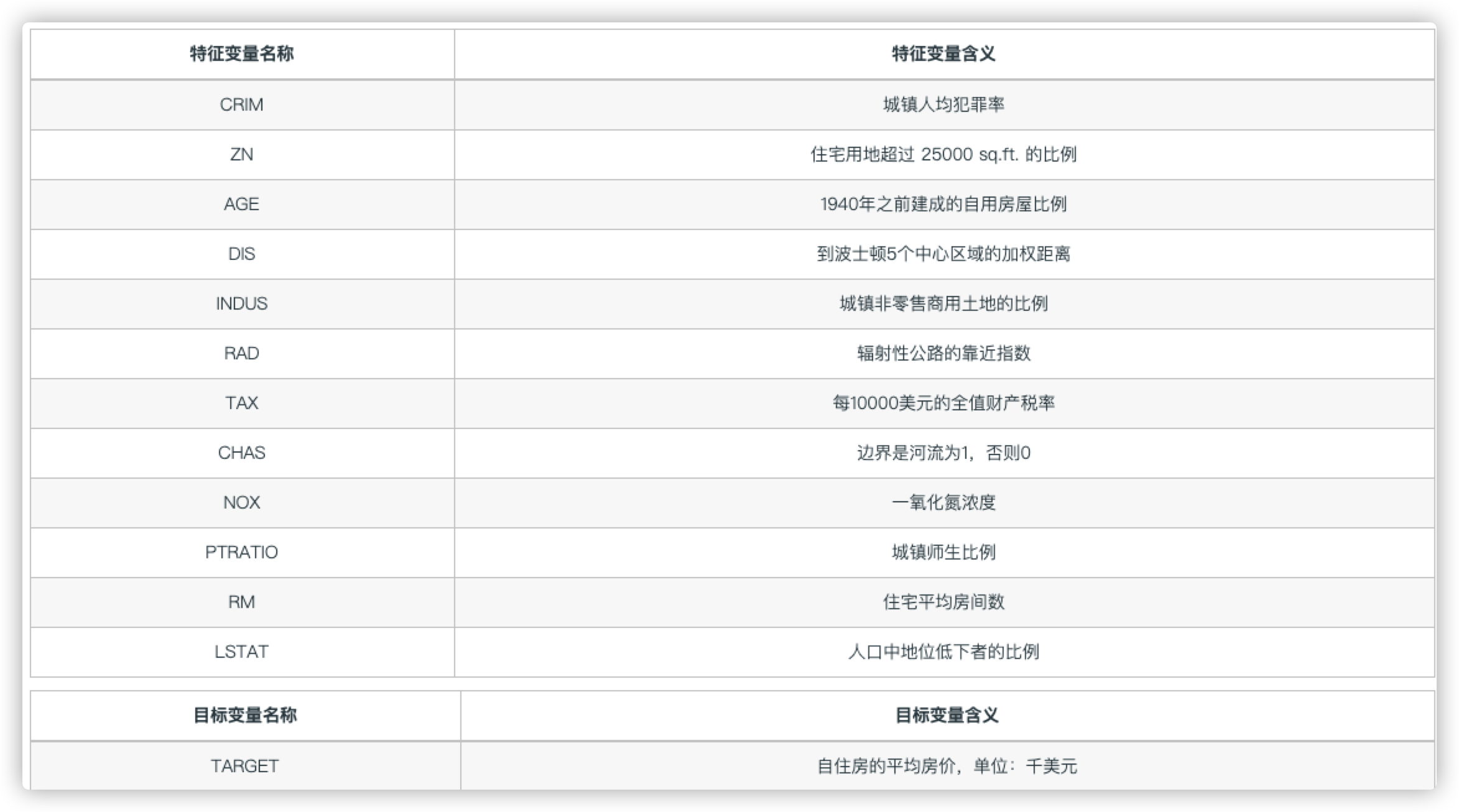
可以看到,研究者希望找出影响房价的重要因素,比如环境因素(一氧化氮浓度),位置因素(到波士顿 5 个中心区域的加权距离)等等(不过我相信影响中国房价因素要比这复杂的多)
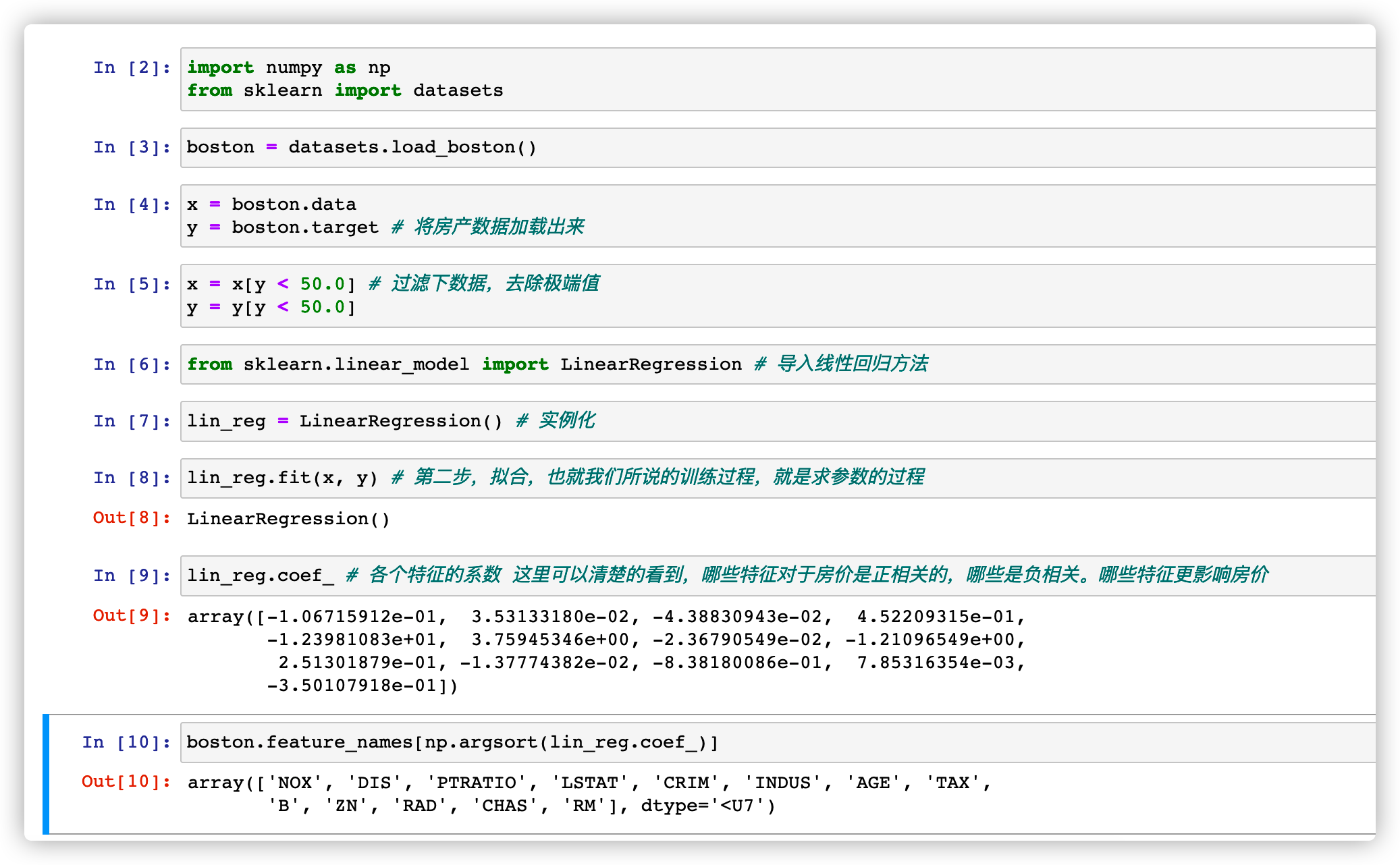
经过求解得出了(或者说学习到了)各个参数的值,然后如果地产商想要定价的话,可以收集这些特征,然后使用模型的 predict 方法可以得出一个房价的参考值。
然后我们也可以看到,哪些因素对于房价是正相关的,哪些是负相关的。然后参数越大,越影响房价,这就是线性回归法对于结果的可解释性(有些机器学习方法是不支持的)。
欢迎关注凹凸实验室博客:aotu.io
或者关注凹凸实验室公众号(AOTULabs),不定时推送文章:


