/*Day1、Day2我尽量整理吧*/
树状数组
树状数组滋瓷单点修改和前缀查询
加特技可以使得树状数组支持更多操作。
c[2n+1]=a[2n+1](奇数就是它本身)
c[2n]≠a[2n](偶数不是)
二进制表示1~8
dec bin 1 0001 2 0010 3 0011 4 0100 5 0101 5 0110 7 0111 8 1000
一个数包含的位数和它二进制最后一个1的位置有关。
c[x]=a[x-lowbit(x)+1]+...+a[x]
-x=2^32-x
lowbit(x)=x&(-x);
莫名其妙地翻到了以前写的博客:
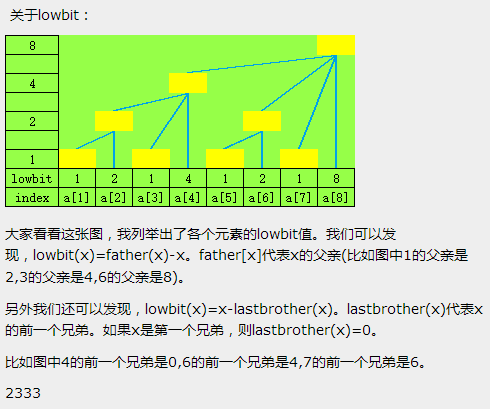
求和:x每次减去lowbit(x)
代码:
void add(int x,int y)//第x项+y
{
for(;x<=n;x+=x&-x)
c[x]+=y;
}
int ask(int x)//第x项的前缀和
int y=0;
for(;x;x-=x&-x)
y+=c[x];
return y;
}
复杂度均为:O(log2n)
NOIP2013 火柴排队

匹配方法:按照排序位置匹配
让a中第k大和b中比k大匹配
同时移动a,b与只移动一个没有区别,可以确定一个移动一个。
首先:离散化:Ai表示ai是a数组第几大的,Bi表示bi是b数组中第几大的
离散化之后,火柴的高度已经没有意义了,只要能够表示出是第几大就行
定义数组C满足C[A[i]]=i,D满足D[i]=C[B[I]],表示b数组的第i项最终需要移动到哪一位
然后求D数组中的逆序对数即可。前后枚举每一项,用树状数组维护D
int main()
{
for(i=1;i<=n;i++)
A[i]=a[i];
sort(a+1,a+n+1);//给a数组从小到大排序
for(i=1;i<=n;i++)
A[i]=lower_bound(a+1,a+n+1,A[i])-a;
//通过lower_bound搜到A[i](原来的a[i])在排序后的数组中的排名是第几小的
for(i=1;i<=n;i++)
B[i]=b[i];
sort(b+1,b+n+1);
for(i=1;i<=n;i++)
B[i]=lower_bound(b+1,b+n+1,B[i])-b;
//B[i]同A[i]
//A[i]表示a[i]是a数组中第几小的 ——hzh
//C[i]表示a数组第i小的数的下标 ——hzh
for(i=1;i<=n;i++)C[A[i]]=i;//C[i]表示a数组第i小的数的下标
for(i=1;i<=n;i++)D[i]=C[B[i]];//B[i]是b[i]的排名
//C[B[i]]是b[i]对应的排名相等a[i]下标;即D[i]是b[i]对应的a[i]的位置
//C[B[i]]表示a数组中第B[i]小的数的下标 ——hzh
//D[i]表示b数组中第i个数应该移动到哪个位置 ——hzh
}
然后用计数排序的思想求逆序对:
当D数组遍历到i的时候,我们要找的就是在D数组中i的右边且小于i的元素数量。此时所有在D数组i的右边元素的树状数组中已经标记了个"1"(默认0),而所有小于i的元素在树状数组中都在i的左边。所以,我们只需要求树状数组中i的前缀和,就是D数组中i的右边且小于i的元素的数量。然后把这个结果更新到ans中(ans+=ask(i))。遍历完i后,在树状数组中的i标记一个1(add(i,1)),然后遍历i-1。
野鸡题(实为http://poj.org/problem?id=3468)
区间价一个数,区间求和

差分:
区间加一个数,单点求值的树状数组(差分)
差分:一项减去前一项
代码:配套前面的树状数组代码用
add(l,x); add(r+1,-x);//区间[l,r]增加x权值 ask(x);//查询x点的权值
野鸡题:两个树状数组解决 贼难!!
0 0 0 0 0//初始值
[2,4]+3
0 3 3 3 0 //修改后的值
0 3 6 9 9 //修改后的前缀和
-3 0 0 12 0 //第一个树状数组
-3 -3 -3 9 9 //第一个树状数组前缀和
3 0 0 -3 0 //第二个树状数组:对第一个树状数组的错误进行修正
3 3 3 0 0 //第二个树状数组前缀和
3 6 9 0 0 //第二个树状数组每一项前缀和乘以下标
0 3 6 9 9 //乘以下标之后加上第一个树状数组的前缀和
add(l,r,x)
{
add1(l-1,-x*(l-1));
add1(r,x*r);
add2(l-1,x);
add2(r,-x);
}
ask(l,r)=ask1(r)+ask2(r)*r-(ask1(l-1)+ask2(l-1)*(l-1))
bzoj1878 SDOI2009 HH的项链
用离线的方法做,把所有询问按照一定的顺序做,按照r从小到大排序
1 2 5 2 3 3 5
以代码为生的我
for(i=1;i<=n;i++)
{
f[i]=g[a[i]];
g[a[i]]=i;//处理f数组
add(f[i]+1,1);
add(i+1,-1);//区间[f[i]+1,i]增加1
for(;q[j].r==i&&j<=n;j++)
q[j].ans=ask(q[j].l);//处理询问
}
O(nlog2n)
二叉搜索树——BST(也叫作平衡树)
左儿子<根节点<右儿子,左子树和右子树也是二叉搜索树
treap.每个节点有一个随机的额外权值,这个随机权值满足堆的性质
treap的旋转 右旋、左旋
旋转不改变平衡的性质,堆的随机权值是为了保持平衡
代码
void rotate(int x)
{
int y=dad[x],z=dad[y];
bool f=s[1][y]==x;
if(!is_root(y))s[s[1][z]==y][z]=x;
s[f][y]=s[!f][x];s[!f][x]=y;
dad[x]=z;dad[y]=x;dad[s[f][y]]=y;
update(x);update(y);
}
Afternoon!
treap 有两个权值,一个平衡树的权值;一个堆的权值;性质(略)
在保证两个权值唯一相等,这个数是唯一确定的(!?!??!!??!?!)
旋转操作:P是Q左儿子->右旋->Q是P右儿子
Q是P右儿子->P是Q的左儿子
旋转之后,中序遍历是一样的,且满足平衡树的性质
如何满足堆的性质?
加入一个点 ——(x,?)
从root开始“二分查找”,钦点(x,?)的位置
为了满足堆的性质,判断是怎样交换节点,要左旋还是右旋
然后转来转去把它转成treap
treap代码
void left_rotate(int &q,int p)//
{
rs[q]=ls[p];
ls[p]=q;
q=p;
}
void right_rotate(int &q,int p)//
{
ls[q]=rs[p];
rs[p]=q;
q=p;
}
void add(int x,int &cur)
{
if(!cur)
{
cur=++cnt;
V[cnt]=x;
R[cnt]=rand();
return;
}
if(x>V[cur])
{
add(x,rs[cur]);
if(R[rs[cur]]<R[cur])
left_rotate(cur,rs[cur]);
}
else
{
add(x,ls[cur]);
if(R[ls[cur]]<R[cur])
right_rotate(cur,ls[cur]);
}
}
void del(int x,int &cur)
{
if(V[cur]==x)
{
if(!ls[cur]||!rs[cur])
{
cur=ls[cur]|rs[cur];
return;
}
if(R[ls[cur]]>R[rs[cur]])
{
left_rotate(cur,rs[cur]);
del(x,ls[cur]);
}
else
{
right_rotate(cur,ls[cur]):
del(x,rs[cur]);
}
}
else
if(x<V[cur])del(x,ls[cur]);
else
del(x,rs[cur]);
}
Splay
Zig-Zig操作
Zig-Zag操作
添加节点:
和treap类似,在过程中不需要rotata,再查完之后需要将插入的元素进行一遍splay(整个做完add之后再splay,是并列的不是套着的)
删除元素:
如果这元素只有一儿子,让这儿子当做他
如果有两个儿子;从左子树找最大的或者右子树找最小的
代码:太难了
void splay(int x)
{
st[t=1]=x;
for(int y=x;!is_root(y);st[++t]=y=dad[y]);
for(;t;t--)if(rev[st[t]])reverse(st[t]);
for(;!is_root(x);rotate(x))if(!is_root(dad[x]))
s[0][dad[x]]==x^s[0][dad[dad[x]]]==dad[x]?rotate(x):rotate(dad[x]);
update(x);
}
int find_max(int cur)
{
for(;s[1][cur];cur=s[1][cur]);
return cur;
}
void combine(int &cur,int cur1)
{
cur=find_max(cur);//找到一棵树最大的节点
splay(cur);
rs[cur]=cur1;
}
fhq-treap(不讲)
替罪羊树
朝鲜树:不旋转 add找到在哪里插,然后直接插进去

玄学的替罪羊树:最快的平衡树.........媲美RBT(msRBT更快????)
Problem:bzoj3224/bzoj3223
STL
pair(对) pair<int,int> make_pair(x,y) sort排序用
priority_queue(堆)
priority_queue<pair<int,int> >q;//两个>之间有个空格
map 映射(hash) 红黑树 定义:map<int,int>a; 赋值:a[x]=y; 取值:cout << a[x];
set 功能:insert upper_bound lower_bound size clear begin end 迭代器支持++ --
multiset 删除一个数会把所有这个数删掉
bitset<数>Bit; bit[数]=1; bit<<=100; (int)bit[xxx]; count() O(n) size没用 reset有用 flip 转位 bit=~Bit也可
线段树
直接放代码一波(+lazy tag的)
#include <bits/stdc++.h>
using namespace std;
void pushdown(int cur,int x)
{
cov[cur<<1]+=cov[cur];
cov[cur<<1|1]+=cov[cur];
sum[cur<<1]+=cov[cur]*(x+1>>1);
sum[cur<<1|1]+=cov[cur]*(x>>1);
cov[cur]=0;
}
void update(int cur)
{
sum[cur]=sum[cur<<1]+sumpcur<<1|1];
}
void add(int l,int r,int L,int R,int x,int cur)
{
if(L=<l&&R>=r)
{
cov[cur]+=x;
sum[cur]+=(r-l+1)*x;
return x;
}
if(cov[cur])
pushdown(cur,r-l+1);
int mid=l+r>>1;
if(L<=mid)
add(l,mid,L,R,x,cur<<1);
if(R>mid)
add(mid+1,r,L,R,x,cur<<1|1);
update(cur);
}
int query(int l,int r,int L,int R,int cur)
{
if(L<=l&&R>=r)
return sum[cur];
if(cov[cur])
pushdown(cur,r-l+1);
int mid=l+r>>1,ans=0;
if(L<=mid)
ans+=query(l,mid,L,R,cur<<1|1);
return ans;
}
problems:
tyvj1473 校门外的树3
开两个线段树,一个存左边界另一个存右边界,m-2的时候求[1,l-1]之间的右边界数【求得是左边不再要查找区间内的线段数】ans1和[r+1,n]的左边界数【求的是右边不在要查找区间内的线段树】ans2,ans=tot_line-ans1-ans2
codevs1299:切水果
N个东西,每次标记[L,R]的东西,并求出没有被标记的数量
对于线段树上每个节点维护sum标记,表示这个节点对应区间中剩下水果数量。每次输出sum[1] 时间复杂度O(nlog2n)
bzoj4373
区间组成等差数列条件:
max[l,r]-min[l,r]=(r-l)*k.
差分gcd=k
修改:把他与前后两个数差分改了就行
最大值和最小值不能用ST表,请用线段树,因为他要修改
时间复杂度=O(nlog22n)
trie树(踹树???)
字典树、单词查找树
三个基本性质
根节点不包含字符,除了根节点外每一个节点都只包含一个字符。
从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串
每个节点的所有子节点所有包含的字符不相同
踹树是“26叉树”,只是一些没有儿子的节点我们会忽略(就是不需要的字符忽略掉)
代码:
#include <bits/stdc++.h>
using namespace std;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%s",s[i]+1);
m=strlen(s[i]+1);
for(j=1,cur=root;j<=m;j++)
if(son[cur][s[j]-'a'])
cur=son[cur][s[j]-'a'];
else
cur=son[cur][s[j]-'a']=++cnt;
tot[cur]++;
}
}
于是他错误的点名开始了????这什么破题目名字
luogu2580
#include<bits/stdc++.h>
using namespace std;
int main(){
scanf("%d",&n);
root=1;
for(i=1;i<=n;i++){
scanf("%s",s+1);
m=strlen(s+1);
for(j=1,cur=root;j<=m;j++)
if(son[cur][s[j]-'a'])cur=son[cur][s[j]-'a'];
else cur=son[cur][s[j]-'a']=++cnt;
tot[cur]=1;
}
scanf("%d",&m);
for(i=1;i<=n;i++){
scanf("%s",s+1);
m=strlen(s+1);
for(j=1,cur=root;j<=m;j++)
cur=son[cur][s[j]-'a'];
if(tot[cur]==1)puts("OK"),tot[cur]=-1;
else if(tot[cur]==-1)puts("REPEAT");
else puts("WRONG");
}
}
luogu2292 L语言
字典建踹树,然后一个一个字符匹配去吧。。。O(n*m)
Luogu2922 秘密消息
信息建踹树,一个节点的标记表示以这个节点为结尾的信息数量,然后每个密码从根节点遍历,遍历到头之后求经过路径的标记和,然后求以这个节点为子树的标记和
BZOJ3261 最大异或和
用前缀异或建踹树,
函数式线段树
president树
可持久化线段树(可反悔线段树)
主席树:
void add(int l,int r,int x,int y,int &cur,int cur1)
{
cur=++cnt;
sum[cur]=sum[cur1]+y;
ls[cur]=ls[cur1];
rs[cur]=rs[cur1];
if(l==r)
return;
int mid=l+r>>1;
if(x<=mid)
add(l,mid,x,y,ls[cur],ls[cur1]);
else
add(mid+1,r,x,y,rs[cur],rs[cur1]);
}
int ask(int l,int r,int k,int cur,int cur1)
{
if(l==r)return l;
int mid=l+r>>1;
if(sum[ls[cur]]-sum[ls[cur1]]>=k)
return ask(l,mid,k,ls[cur],ls[cur1]);
else
return ask(mid+1,r,k-sum[ls[cur]]+sum[ls[cur1]],rs[cur],rs[cur1]);
}
int main()
{
for(i=1;i<=n;i++)
{
scanf("%d%d",&x,&y);
add(1,n,x,y,root[i],root[i-1]);
ask(1,n,k,root[r],root[l-1]);
}
}
空间:nlog2n

来自:http://www.jianshu.com/p/e6050f01c4bc
字符串hash MD5
字符串转换成高进制大整数
hash:大数/巨数(或字符串)变比较小的
01串翻转问题(课件P450)
代码:
#include<bits/stdc++.h>
using namespace std;
int main(){
scanf("%d",&n);
for(i=0;i<n;i++)scanf("%d",&x),a[i]=x;
scanf("%d",&t);
for(i=1;i<=t;i++){
scanf("%d",&l[i]);
for(j=0;j<l[i];j++)scanf("%d",&x),b[i][j]=x;
}
scanf("%d",&m);
f[0][0]=1;
for(i=1;i<n;i++)
f[i]=f[i-1],f[i][i]=1;
while(m--){
scanf("%d%d%d",&s,&l,&r);
if(s==1){
a^=f[r-1];
if(l-1)a^=f[l-2];
}else
{
scanf("%d",&p);
c=a;
if(l-1)c>>=l-2;
c&=f[l[i]-1];
if((c^b[p]).count())puts("NO");
else puts("YES");
}
}
}
完。