(color{#0066ff}{题目描述})
在一个 n*n个方格的国际象棋棋盘上,马(骑士)可以攻击的棋盘方格如图所示。棋盘上某些方格设置了障碍,骑士不得进入
对于给定的 n*n 个方格的国际象棋棋盘和障碍标志,计算棋盘上最多可以放置多少个骑士,使得它们彼此互不攻击
(color{#0066ff}{输入格式})
第一行有 2 个正整数n 和 m ((1<=n<=200, 0<=m<n^2)),分别表示棋盘的大小和障碍数。接下来的 m 行给出障碍的位置。每行 2 个正整数,表示障碍的方格坐标。
(color{#0066ff}{输出格式})
将计算出的共存骑士数输出
(color{#0066ff}{输入样例})
3 2
1 1
3 3
(color{#0066ff}{输出样例})
5
(color{#0066ff}{数据范围与提示})
nothing
(color{#0066ff}{题解})
最大流等于最小割定理
合法情况下,总情况-不成立情况=成立情况
因为最小割等于最大流,所以找到不成立情况的最大流
就得到了答案
现在我们要找不合法情况的最大流
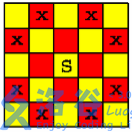
考虑上图的红黄点,一个红点被占据,只会影响黄点,黄点同理
因此,S向所有红点连容量为 1 的边
所用红点向其影响的黄点连容量为 inf 的边(保证被影响,求出所有不合法情况
所有黄点向T连容量为 1 的边
答案就是n*n-m-最大流
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cmath>
#define _ 0
#define LL long long
inline LL in()
{
LL x=0,f=1; char ch;
while(!isdigit(ch=getchar()))(ch=='-')&&(f=-f);
while(isdigit(ch)) x=x*10+(ch^48),ch=getchar();
return x*f;
}
const int inf=0x7fffffff;
struct node{int to,nxt,dis;}e[1050050];
int rx[]={-2,-2,-1,-1,1,1,2,2};
int ry[]={-1,1,-2,2,-2,2,-1,1};
int cnt=1,n,m,s,t;
std::queue<int> q;
int head[505005],cur[505005],dep[500505];
bool mp[250][250];
inline int getid(int x,int y) {return (x-1)*n+y;}
inline void add(int from,int to,int dis)
{
cnt++;
e[cnt].to=to;
e[cnt].dis=dis;
e[cnt].nxt=head[from];
head[from]=cnt;
}
inline void expand(int x,int y)
{
for(int i=0;i<8;i++)
{
int xx=x+rx[i];
int yy=y+ry[i];
if(xx>=1&&xx<=n&&yy>=1&&yy<=n&&!mp[xx][yy])
{
add(getid(x,y),getid(xx,yy),inf);
add(getid(xx,yy),getid(x,y),0);
}
}
}
inline bool bfs()
{
for(int i=s;i<=t;i++) dep[i]=0,cur[i]=head[i];
q.push(s);
dep[s]=1;
while(!q.empty())
{
int tp=q.front(); q.pop();
for(int i=head[tp];i;i=e[i].nxt)
{
int go=e[i].to;
if(!dep[go]&&e[i].dis>0)
{
dep[go]=dep[tp]+1;
q.push(go);
}
}
}
return dep[t];
}
inline int dfs(int x,int change)
{
if(x==t||!change) return change;
int flow=0,ls;
for(int i=cur[x];i;i=e[i].nxt)
{
int go=e[i].to;
cur[x]=i;
if(dep[go]==dep[x]+1&&(ls=dfs(go,std::min(change,e[i].dis))))
{
change-=ls;
flow+=ls;
e[i].dis-=ls;
e[i^1].dis+=ls;
if(!change) break;
}
}
return flow;
}
inline int dinic()
{
int flow=0;
while(bfs()) flow+=dfs(s,inf);
return flow;
}
int main()
{
n=in(),m=in();
t=n*n+1,s=0;
int x,y;
for(int i=1;i<=m;i++)
{
x=in(),y=in();
mp[x][y]=true;
}
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++)
{
if(mp[i][j]) continue;
if((i+j)&1)
{
add(s,getid(i,j),1);
add(getid(i,j),s,0);
expand(i,j);
}
else add(getid(i,j),t,1),add(t,getid(i,j),0);
}
printf("%d",n*n-m-dinic());
return 0;
}