(color{#0066ff}{题目描述})
Linux用户和OSX用户一定对软件包管理器不会陌生。通过软件包管理器,你可以通过一行命令安装某一个软件包,然后软件包管理器会帮助你从软件源下载软件包,同时自动解决所有的依赖(即下载安装这个软件包的安装所依赖的其它软件包),完成所有的配置。Debian/Ubuntu使用的apt-get,Fedora/CentOS使用的yum,以及OSX下可用的homebrew都是优秀的软件包管理器。
你决定设计你自己的软件包管理器。不可避免地,你要解决软件包之间的依赖问题。如果软件包A依赖软件包B,那么安装软件包A以前,必须先安装软件包B。同时,如果想要卸载软件包B,则必须卸载软件包A。现在你已经获得了所有的软件包之间的依赖关系。而且,由于你之前的工作,除0号软件包以外,在你的管理器当中的软件包都会依赖一个且仅一个软件包,而0号软件包不依赖任何一个软件包。依赖关系不存在环(若有m(m≥2)个软件包A1,A2,A3,⋯,Am,其中A1依赖A2,A2依赖A3,A3依赖A4,……,A[m-1]依赖Am,而Am依赖A1,则称这m个软件包的依赖关系构成环),当然也不会有一个软件包依赖自己。
现在你要为你的软件包管理器写一个依赖解决程序。根据反馈,用户希望在安装和卸载某个软件包时,快速地知道这个操作实际上会改变多少个软件包的安装状态(即安装操作会安装多少个未安装的软件包,或卸载操作会卸载多少个已安装的软件包),你的任务就是实现这个部分。注意,安装一个已安装的软件包,或卸载一个未安装的软件包,都不会改变任何软件包的安装状态,即在此情况下,改变安装状态的软件包数为0。
(color{#0066ff}{输入格式})
从文件manager.in中读入数据。
输入文件的第1行包含1个整数n,表示软件包的总数。软件包从0开始编号。
随后一行包含n−1个整数,相邻整数之间用单个空格隔开,分别表示1,2,3,⋯,n−2,n−1号软件包依赖的软件包的编号。
接下来一行包含1个整数q,表示询问的总数。之后q行,每行1个询问。询问分为两种:
install x:表示安装软件包x
uninstall x:表示卸载软件包x
你需要维护每个软件包的安装状态,一开始所有的软件包都处于未安装状态。
对于每个操作,你需要输出这步操作会改变多少个软件包的安装状态,随后应用这个操作(即改变你维护的安装状态)。
(color{#0066ff}{输出格式})
输出到文件manager.out中。
输出文件包括q行。
输出文件的第i行输出1个整数,为第i步操作中改变安装状态的软件包数。
(color{#0066ff}{输入样例})
1、
7
0 0 0 1 1 5
5
install 5
install 6
uninstall 1
install 4
uninstall 0
2、
10
0 1 2 1 3 0 0 3 2
10
install 0
install 3
uninstall 2
install 7
install 5
install 9
uninstall 9
install 4
install 1
install 9
(color{#0066ff}{输出样例})
1、
3
1
3
2
3
2、
1
3
2
1
3
1
1
1
0
1
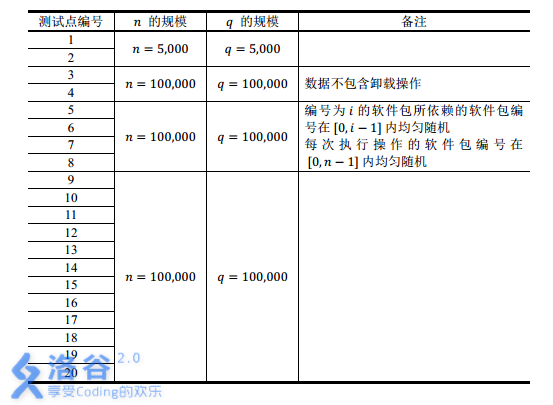
(color{#0066ff}{数据范围与提示})
(color{#0066ff}{题解})
关于查询,一个是到根的0的个数(跳top), 一个是子树查询(线段树直接修改)
修改同上,注意特判0
#include <bits/stdc++.h>
#define LL long long
const int maxn = 1e5 + 20;
LL in() {
char ch; int x = 0, f = 1;
while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
return x * f;
}
struct node {
int to;
node *nxt;
node(int to = 0, node *nxt = NULL) : to(to), nxt(nxt) {}
void *operator new (size_t) {
static node *S = NULL, *T = NULL;
return (S == T) && (T = (S = new node[1024]) + 1024), S++;
}
};
struct sgt {
int l, r;
int val, tag;
sgt *ch[2];
sgt(int l = 0, int r = 0, int val = 0, int tag = -1) : l(l), r(r), val(val), tag(tag) {}
void *operator new (size_t) {
static sgt *S = NULL, *T = NULL;
return (S == T) && (T = (S = new sgt[1024]) + 1024), S++;
}
int siz() {return r - l + 1;}
void upd() { val = ch[0]->val + ch[1]->val;}
void dwn() {
if(!(~tag)) return;
ch[0]->tag = tag;
ch[1]->tag = tag;
ch[0]->val = tag? ch[0]->siz() : 0;
ch[1]->val = tag? ch[1]->siz() : 0;
tag = -1;
}
};
int dep[maxn], son[maxn], top[maxn], siz[maxn], dfn[maxn], fa[maxn];
int cnt, n, q;
node *head[maxn];
sgt *root;
void add(int from, int to) {
node *o = new node(to, head[from]);
head[from] = o;
}
void dfs1(int x, int f) {
fa[x] = f;
dep[x] = dep[f] + 1;
siz[x] = 1;
for(node *i = head[x]; i; i = i->nxt) {
if(i->to == f) continue;
dfs1(i->to, x);
siz[x] += siz[i->to];
if(!son[x] || siz[i->to] > siz[son[x]]) son[x] = i->to;
}
}
void dfs2(int x, int t) {
top[x] = t;
dfn[x] = ++cnt;
if(son[x]) dfs2(son[x], t);
for(node *i = head[x]; i; i = i->nxt)
if(!dfn[i->to]) dfs2(i->to, i->to);
}
void build(sgt *&o, int l, int r) {
o = new sgt(l, r, 0, -1);
if(l == r) return;
int mid = (l + r) >> 1;
build(o->ch[0], l, mid);
build(o->ch[1], mid + 1, r);
o->upd();
}
void lazy(sgt *o, int l, int r, int k) {
if(o->r < l || o->l > r) return;
if(l <= o->l && o->r <= r) {
o->val = k? o->siz() : 0;
o->tag = k;
return;
}
o->dwn();
lazy(o->ch[0], l, r, k), lazy(o->ch[1], l, r, k);
o->upd();
}
int query(sgt *o, int l, int r) {
if(o->r < l || o->l > r) return 0;
if(l <= o->l && o->r <= r) return o->val;
o->dwn();
return query(o->ch[0], l, r) + query(o->ch[1], l, r);
}
char getch() {
char ch;
while(!isalpha(ch = getchar()));
return ch;
}
int querypath(int x) {
int ans = 0;
int fx = top[x];
while(x) {
fx = top[x];
ans += query(root, dfn[fx], dfn[x]);
x = fa[fx];
}
return ans;
}
void addpath(int x) {
int fx = top[x];
while(x) {
fx = top[x];
lazy(root, dfn[fx], dfn[x], 1);
x = fa[fx];
}
}
int main() {
n = in();
int x;
for(int i = 1; i < n; i++) {
x = in();
x = x? x : n;
add(i, x), add(x, i);
}
dfs1(n, 0);
dfs2(n ,n);
build(root, 1, n);
q = in();
while(q--) {
if(getch() == 'i') {
x = in();
x = x? x : n;
if(query(root, dfn[x], dfn[x])) goto noans;
printf("%d
", dep[x] - querypath(x));
addpath(x);
}
else {
x = in();
x = x? x : n;
if(!query(root, dfn[x], dfn[x])) goto noans;
printf("%d
", query(root, dfn[x], dfn[x] + siz[x] - 1));
lazy(root, dfn[x], dfn[x] + siz[x] - 1, 0);
}
continue;
noans:;
puts("0");
}
return 0;
}