(color{#0066ff}{ 题目描述 })
兔子们决定在自己的城堡里安排一些士兵进行防守。
给出 n 个点的坐标,和城堡里一个圆心在原点的圆形的障碍,兔子们希望从中选出 k 个兔子,使得它们两两所在的直线都不与圆相交。
兔子们希望知道最多能选出多少兔子。
(color{#0066ff}{输入格式})
第一行两个整数 N 和 R, 表示兔子的个数和圆的半径接下来 N 行,每行两个整数 xi 和 yi ,表示第 i 只兔子的坐标
保证每只兔子都严格在障碍外部,且两两的所在的直线不与圆相切。
(color{#0066ff}{输出格式})
输出一行一个整数, 表示最多能选出多少兔子
(color{#0066ff}{输入样例})
6 3
0 6
-7 -4
-3 -2
7 -5
-2 3
8 -3
(color{#0066ff}{输出样例})
4
(color{#0066ff}{数据范围与提示})
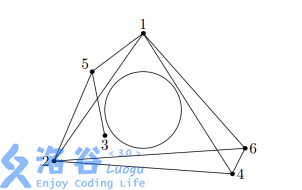
选择第 1, 2, 6, 4 只兔子即可。
- 对于 10% 的测试数据, 1 ≤ n ≤ 20.
- 对于 30% 的测试数据, 1 ≤ n ≤ 100.
- 对于 100% 的测试数据, 1 ≤ n ≤ 2000; 1 ≤ R; xi; yi ≤ 5000.
(color{#0066ff}{ 题解 })
过每一个点做圆的两条切线,每个点占据了圆上的一段劣弧
不难发现,两个点的连线与圆有交,当且仅当两段劣弧不相离且互补包含,即普通的相交
于是我们开始想办法获得这个劣弧
我们该怎么存储这种东西呢
考虑把环断开,以极角作为链上的数值,强制让线段范围为([-pi,pi]),对于不在这个范围上的端点,可以直接(+-2pi),显然没影响
那么怎么获得这两个端点值(角度)呢
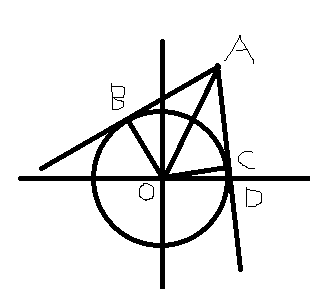
∠AOB=∠AOC, 因此只要让极角∠AOD加减∠AOB即可获得端点值
然后我们把所有区间按左端点排序
然后枚举每个区间作为选择的起始区间,枚举之后选择的区间,那之后选择的区间要满足左端点小于起始区间右端点,右端点大于起始区间右端点,这样才是相交
我们把这些区间放在数组里,左端点是递增的且一定小于起始区间右端点
那么可以发现,最多选择的数量就是这些区间右端点的最长上升子序列!
于是(O(n^2logn))即可解决本题
#include<bits/stdc++.h>
#define LL long long
LL in() {
char ch; LL x = 0, f = 1;
while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
return x * f;
}
const int maxn = 2050;
const double pi = acos(-1);
using std::pair;
using std::make_pair;
int n;
double R;
pair<double, double> e[maxn];
int num, ans;
double f[maxn], t[maxn];
int query() {
int len;
if(!num) return 0;
f[len = 1] = t[1];
for(int i = 2; i <= num; i++) {
if(t[i] > f[len]) f[++len] = t[i];
else *std::upper_bound(f + 1, f + len + 1, t[i]) = t[i];
}
return len;
}
int main() {
n = in(), R = in();
double x, y;
for(int i = 1; i <= n; i++) {
x = in(), y = in();
double bt = atan2(y, x);
double len = sqrt(x * x + y * y);
double af = acos(R / len);
x = bt - af, y = bt + af;
while(x <= -pi) x += 2.0 * pi;
while(y > pi) y -= 2.0 * pi;
if(x > y) std::swap(x, y);
e[i] = make_pair(x, y);
}
std::sort(e + 1, e + n + 1);
for(int i = 1; i <= n; i++) {
num = 0;
for(int j = i + 1; j <= n; j++)
if(e[j].first <= e[i].second && e[j].second >= e[i].second)
t[++num] = e[j].second;
ans = std::max(ans, query());
}
printf("%d", ans + 1);
return 0;
}