P5108 仰望半月的夜空 SAM+线段树覆盖

$ color{#0066ff}{ 题目描述 }$

半月的夜空中，寄托了多少人与人之间的思念啊

曦月知道，这些思念会汇集成一个字符串(S(n = |S|))

由于思念汇集的过于复杂，因此曦月希望提炼出所有的思念

我们定义(Y_S(i))表示对于字符串(S)而言，长度为(i)的子串中，字典序最小的，左端点最小的左端点的值

比如对于串(S = "baa")，(Y_S(1) = 2, Y_S(2) = 2, Y_S(3) = 1)

曦月会告知你(S)串，你只需要告诉曦月(Y_S(i)(1 le i le n))即可

(color{#0066ff}{输入格式})

第一行，两个参数，分别是(sigma in {10, 26, 10^7})和(n)

如果(sigma = 26)，那么第二行将是一个长为(n)的小写字母字符串(S)

其他情况下，第二行将输入(n)个位于([0, sigma]内)的整数

(color{#0066ff}{输出格式})

输出一行，第iii个数表示(Y_S(i))的值

(color{#0066ff}{输入样例})

26 11
remoonqaqac

26 11
txdydkwqaqa


10000000 17
9 9 8 2 4 4 3 5 3 1 9 2 6 0 8 1 7

(color{#0066ff}{输出样例})

8 10 8 8 2 2 2 2 2 2 1
    
9 9 9 5 5 5 5 3 3 1 1
   
14 14 14 14 10 10 10 10 4 4 4 4 4 4 3 2 1

(color{#0066ff}{数据范围与提示})

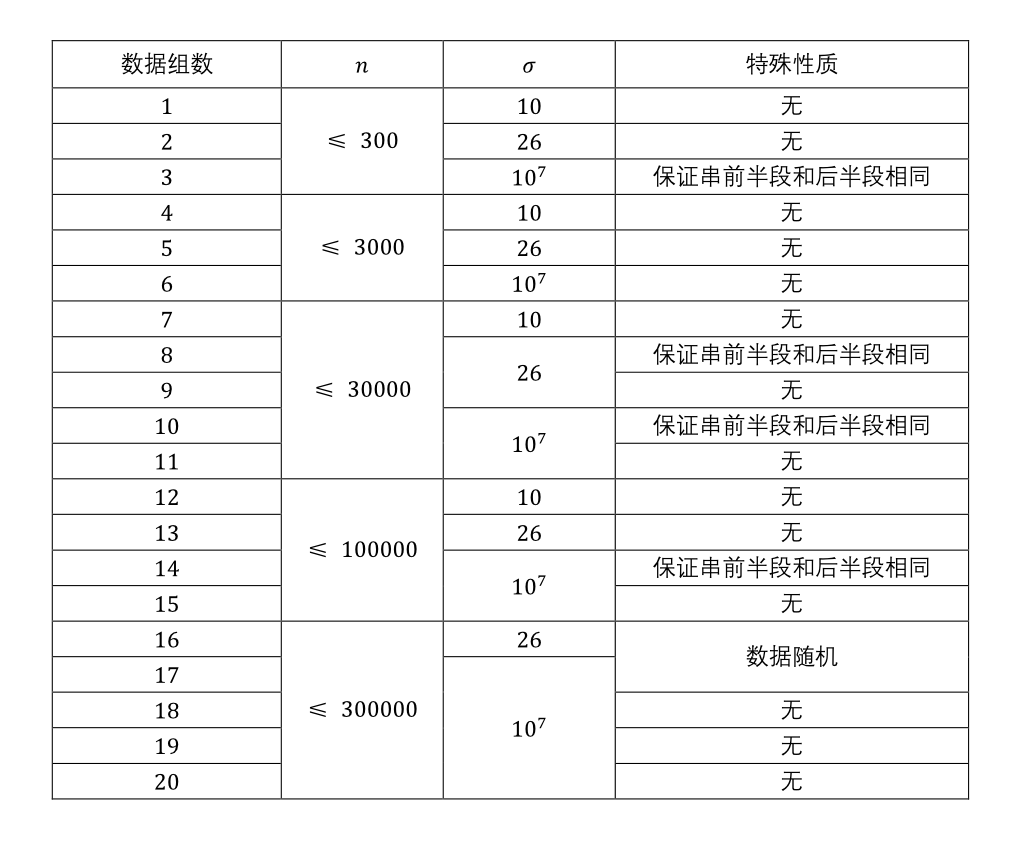
(color{#0066ff}{题解})

建立后缀自动机，要求左端点最小，你需要维护左端点，所以倒着插入，建立后缀树

这样树上的点代表的是某一后缀的前缀

后缀自动机上每个点维护一个pos为起始位置l

然后考虑后缀树上的一条边，它对应的字串长度就是$[父亲len+1，自己的len] $，那么对于这一区间的答案就可以用自己子树的pos最小值来更新

至于字典序最小?，我们可以dfs出后缀树中每个节点是它父亲的那个儿子，然后考虑倒着覆盖，当前字典序是最优的，把原来的覆盖掉，用线段树维护答案就行了

#include<bits/stdc++.h>
#define LL long long
LL in() {
	char ch; LL x = 0, f = 1;
	while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
	return x * f;
}
const int maxn = 3e5 + 10;
const int inf = 0x7fffffff;
struct Tree {
	protected:
		struct node {
			node *ch[2];
			int l, r, val, tag;
			node(int l = 0, int r = 0, int val = 0, int tag = -1): l(l), r(r), val(val), tag(tag) {
				ch[0] = ch[1] = NULL;
			}
			void trn(int v) { val = tag = v; }
			void dwn() {
				if(tag == -1) return;
				ch[0]->trn(tag);
				ch[1]->trn(tag);
				tag = -1;
			}
			int mid() { return (l + r) >> 1; }
		}*root;
		void build(node *&o, int l, int r) {
			o = new node(l, r);
			if(l == r) return;
			build(o->ch[0], l, o->mid());
			build(o->ch[1], o->mid() + 1, r);
		}
		void lazy(node *o, int l, int r, int val) {
			if(l > r) return;
			if(l <= o->l && o->r <= r) return o->trn(val);
			o->dwn();
			if(l <= o->mid()) lazy(o->ch[0], l, r, val);
			if(r > o->mid()) lazy(o->ch[1], l, r, val);
		}
		void out(node *o) {
			if(o->l == o->r) return (void)(printf("%d ", o->val));
			o->dwn();
			out(o->ch[0]); out(o->ch[1]);
		}
	public:
		void build(int n) { build(root, 1, n); }
		void lazy(int l, int r, int val) { lazy(root, l, r, val); }
		void out() { out(root); }
}tree;
struct SAM {
	protected:
		struct node {
			std::map<int, node*> ch, treech;
			node *fa;
			int len, pos;
			node(int len = 0, int pos = 0): len(len), pos(pos) { 
				fa = NULL;
				ch.clear(), treech.clear();
			}
		}pool[maxn << 1], *tail, *root, *lst;
		int s[maxn];
		char ls[maxn];
		void extend(int c, int id) {
			node *o = new(tail++) node(lst->len + 1, id), *v = lst;
			for(; v && !v->ch[c]; v = v->fa) v->ch[c] = o;
			if(!v) o->fa = root;
			else if(v->len + 1 == v->ch[c]->len) o->fa = v->ch[c];
			else {
				node *n = new(tail++) node(v->len + 1, v->ch[c]->pos), *d = v->ch[c];
				n->ch = d->ch, n->fa = d->fa, d->fa = o->fa = n;
				for(; v && v->ch[c] == d; v = v->fa) v->ch[c] = n;
			}
			lst = o;
		}
		void getmin(node *o) {
			for(std::pair<int, node*> i : o->treech) {
				getmin(i.second);
				o->pos = std::min(o->pos, i.second->pos);
			}
		}
		void getans(node *o) {
			tree.lazy((o->fa? o->fa->len + 1 : 1), o->len, o->pos);
			for(std::map<int, node*>::reverse_iterator it = o->treech.rbegin(); it != o->treech.rend(); it++)
				getans(it->second);
		}
	public:
		SAM() {
			tail = pool;
			root = lst = new(tail++) node();
		}
		void init(int bel, int len) {
			if(bel == 26) {
				scanf("%s", ls + 1);
				for(int i = 1; i <= len; i++) s[i] = ls[i] - 'a';
			}
			else {
				for(int i = 1; i <= len; i++) s[i] = in();
			}
			for(int i = len; i >= 1; i--) extend(s[i], i); 
		}
		void build() { 
			for(node *o = pool + 1; o != tail; o++)
				o->fa->treech[s[o->pos + o->fa->len]] = o;
		}
		void getmin() { getmin(root); }
		void getans() { getans(root); }
}s;
int main() {
	int val = in(), n = in();
	s.init(val, n);
	tree.build(n);
	s.build();
	s.getmin();
	s.getans();
	tree.out();
	return 0;
}