题意:$n*m$棋盘上$n*m-1$颗棋子,有且只有一个格子为空白格子,每个棋子大小$1*1$
有些棋子可以移动,而有些棋子固定,任何与空白的格子相邻(有公共的边)的格子上的棋子都可以移动到空白格子上。
游戏的目的是把某个指定位置可以活动的棋子移动到目标位置。
现给定棋盘,q个询问,每次给出起始点,目标点,白块的位置,问最少步数,如果到不了输出-1
输入输出样例
3 4 2 0 1 1 1 0 1 1 0 0 1 0 0 3 2 1 2 2 2 1 2 2 2 3 2
2 -1
【输入输出样例说明】
棋盘上划叉的格子是固定的,红色格子是目标位置,圆圈表示棋子,其中绿色圆圈表示目标棋子。
- 第一次游戏,空白格子的初始位置是(3,2)(图中空白所示),游戏的目标是将初始位置在(1,2)上的棋子(图中绿色圆圈所代表的棋子)移动到目标位置(2,2)(图中红色的格子)上。
移动过程如下:
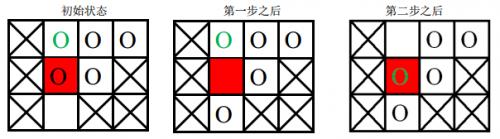
-
第二次游戏,空白格子的初始位置是(1,2)(图中空白所示),游戏的目标是将初始位置在(2,2)上的棋子(图中绿色圆圈所示)移动到目标位置 (3,2)上。
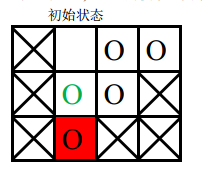
要将指定块移入目标位置,必须先将空白块移入目标位置,空白块要移动到目标位置,必然是从位置(2,2)上与当前图中目标位置上的棋子交换位置,之后能与空白块交换位置的只有当前图中目标位置上的那个棋子,因此目标棋子永远无法走到它的目标位置, 游戏无法完成。
看完题:果断-----爆搜啊
20分。。。。。。TLE QAQ(不过貌似可以70分)
正解:
脑补一下起始棋子移动的画面,起始棋子向终点移动一步,当且仅当空白格子与它相邻且在目标方向上
所以,我们设dis[i][j][k][l][m]表示以i,j为起点,不经过与i,j相邻的m方向上的那个棋子,到各个点的最短路,
考虑一下,白块与起始块交换后,起始块移动了一步,然后白块在起始块原来的位置上,
要想让起始块再向目标前进一步,白块必须在与它相邻且在它目标方向的位置上,再与它交换才行,
而dis数组恰好做到了这一点,找到白块不经过起始块到达起始块目标方向的块的最短路,直接统计,
那一段有居多分支的搜索,我们直接省去了,节省了大量时间
于是,相当于白块带着起始块满图瞎jb乱跑,跑到终点就行了QAQ
#include<cstdio> #include<iostream> #include<cstring> #include<cctype> #include<queue> #include<algorithm> using namespace std; #define int long long #define olinr return #define _ 0 #define love_nmr 0 #define DB double int rx[5]={0,0,0,1,-1}; //四个方向 int ry[5]={0,1,-1,0,0}; int dis[35][35][35][35][5]; //dis[i][j][k][l][m]代表从(i,j)到(k,l)不经过(i,j)m边的那一个格子的最短路(m=上,下,左,右) bool mp[35][35]; //地图 bool viss[35][35]; //spfa的vis bool cop[35][35]; //复制地图 int n; int m; int q; int a,b,c,d,e,f; //空白格子x,y 起始点x,y 终点x,y int ans; //答案 struct node { int x; int y; int dis; }; struct wmy { int dir; int x; int y; int dis; }lv[55]; queue<node> que; int cnt; inline int read() { int x=0,f=1; char ch=getchar(); while(!isdigit(ch)) { if(ch=='-') f=-f; ch=getchar(); } while(isdigit(ch)) { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*f; } inline void put(int x) { if(x<0) { x=-x; putchar('-'); } if(x>9) put(x/10); putchar(x%10+'0'); } inline void spfa(int x,int y,int k) { while(!que.empty()) que.pop(); dis[x][y][x][y][k]=0; que.push((node){x,y,0}); while(!que.empty()) { node tp=que.front(); que.pop(); viss[tp.x][tp.y]=false; for(int i=1;i<=4;i++) { int xx=tp.x+rx[i]; int yy=tp.y+ry[i]; if(xx>=1&&xx<=n&&yy>=1&&yy<=m&&mp[xx][yy]&&dis[x][y][xx][yy][k]>dis[x][y][tp.x][tp.y][k]+1) { dis[x][y][xx][yy][k]=dis[x][y][tp.x][tp.y][k]+1; if(!viss[xx][yy]) { viss[xx][yy]=true; que.push((node){xx,yy,0}); } } } } } inline void bfs() { while(!que.empty()) que.pop(); que.push((node){a,b,0}); cop[a][b]=0; while(!que.empty()) { node tp=que.front(); que.pop(); for(int i=1;i<=4;i++) { int xx=tp.x+rx[i]; int yy=tp.y+ry[i]; if(xx>=1&&xx<=n&&yy>=1&&yy<=m&&cop[xx][yy]) { if(xx==c&&yy==d) { cnt++; //记录白块到起始块的信息 lv[cnt].x=tp.x; lv[cnt].y=tp.y; lv[cnt].dis=tp.dis; lv[cnt].dir=i; } else { cop[xx][yy]=0; que.push((node){xx,yy,tp.dis+1}); } } } } } inline void dfs(int x,int y,int lst1,int lst2,int dir,int tot) { if(tot>=ans) return; if(x==e&&y==f) //找到终点 { ans=tot; return; } mp[x][y]=0; //记为起始块已走过 for(int i=1;i<=4;i++) { int xx=x+rx[i]; int yy=y+ry[i]; if(xx>=1&&xx<=n&&yy>=1&&yy<=m&&mp[xx][yy]&&dis[lst1][lst2][xx][yy][dir]<=1e5) dfs(xx,yy,x,y,i,tot+dis[lst1][lst2][xx][yy][dir]+1); //起始块向目标方向移动距离=白块从原来到现在的距离+1 } mp[x][y]=1; //回溯 } signed main() { n=read(); m=read(); q=read(); memset(dis,1,sizeof dis); //五位数组,赋值1已经很大了 for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) mp[i][j]=read(); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(mp[i][j]) for(int k=1;k<=4;k++) //跑spfa,处理不经过m方向的点的最短路(方法:把那个点变成无法走) { int xx=i+rx[k]; int yy=j+ry[k]; if(xx>=1&&xx<=n&&yy>=1&&yy<=m&&mp[xx][yy]) { mp[xx][yy]=0; spfa(i,j,k); mp[xx][yy]=1; } } while(q--) { cnt=0; for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) cop[i][j]=mp[i][j]; //复制一遍进行操作 a=read(); b=read(); c=read(); d=read(); e=read(); f=read(); if(c==e&&d==f) //起点=终点 { put(0); putchar(' '); continue; } bfs(); //找到初始时空白块到起始块的距离 if(!cnt) //空白块连起始块都到不了QAQ { put(-1); putchar(' '); continue; } ans=0x7ffffffff; //步数初始极大值 for(int i=1;i<=cnt;i++) dfs(c,d,lv[i].x,lv[i].y,lv[i].dir,lv[i].dis); //模拟跑路过程 put(ans==0x7ffffffff? -1:ans); putchar(' '); } olinr ~~(0^_^0)+love_nmr; }