网络流是一个适用范围相当广的模型,相关算法也很多
网络最大流问题
一、定义:假设需要把一些物品从s(源点)运送到t(汇点),可以从其它点中转
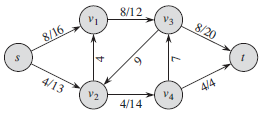
例如上图:$v_2到v_4$最多可以运14个物品,当前运了4个
第二个数字(14)就是上限
我们要求的就是从s最多能有多少物品运送到t
以上就是网络最大流问题
对于一条边,我们记上限为容量:cap
实际运送为流量:flow
不难得出flow(a,b)=-flow(b,a)
也就是说:把flow个物品从a运到b等同于把-flow个物品从b运到a
二、性质:1、容量限制($flow(u,v) le cap(u,v) $)
2、斜对称性($flow(a,b)=-flow(b,a)$)
3、流量平衡:对于除了s和t的节点u $sum_{(u,v) in E}flow(a,b)=0$ (进来的=出去的)QAQ
三、算法实现:
1、Edmonds-Karp算法 $O(m^2n)$
首先,我们定义每条边的残量=这条边的容量-流量
每次,我们跑增广路,从s跑到t,求出这条路上的残量最小值z
然后,让这条路上所有的边都流过z(一定能流过,因为是残量最小值)
让最大流+=z
我们不断跑增广路,直到无法增广,当前一定是最大流
因为一旦存在增广路,最大流就可以再增加
#include<cstdio> #include<iostream> #include<cstring> #include<cctype> #include<vector> #include<queue> #include<algorithm> using namespace std; #define int long long #define olinr return #define _ 0 #define love_nmr 0 #define DB double struct node { int nxt; int to; int cap; int flow; }edge[250505]; int cnt=-1; int head[10505]; int change[10505]; int road[10505]; int n; int m; int s; int t; queue<int>q; inline int read() { int x=0,f=1; char ch=getchar(); while(!isdigit(ch)) { if(ch=='-') f=-f; ch=getchar(); } while(isdigit(ch)) { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*f; } inline void put(int x) { if(x<0) { x=-x; putchar('-'); } if(x>9) put(x/10); putchar(x%10+'0'); } inline void add(int from,int to,int cap,int flow) { cnt++; edge[cnt].to=to; //这条边到的点 edge[cnt].cap=cap; //边的容量 edge[cnt].flow=flow; //边的流量 edge[cnt].nxt=head[from]; //链式前向星。。 head[from]=cnt; } inline int maxflow(int s,int t) //跑最大流 { int flow=0; //最大流 while(5201314+love_nmr) //一直增广直到无法增广 { memset(change,0,sizeof change); //每个点的改变量 while(!q.empty()) q.pop(); q.push(s); change[s]=0x7fffffff; //起点无法增广(最后t的change为一条路的最小残量) while(!q.empty()) //bfs { int tp=q.front(); q.pop(); for(int i=head[tp];i!=-1;i=edge[i].nxt) { int go=edge[i].to; if(!change[go]&&edge[i].cap>edge[i].flow) //没被增广并且有残量 { road[go]=i; //记录路径(最后增广用) change[go]=min(change[tp],edge[i].cap-edge[i].flow); //残量取min q.push(go); } } if(change[t]) break; //成功增广到t(管他从哪条路,反正我到了QAQ) } if(!change[t]) break; //所有路走完依然无法增广 for(int i=t;i!=s;i=edge[road[i]^1].to) //这条边的起点等于反向边的终点 { edge[road[i]].flow+=change[t]; //倒着找回去的路 edge[road[i]^1].flow-=change[t]; //存边技巧,正反互相异或转化(注意从0开始存) } flow+=change[t]; //增广 } return flow; } signed main() { n=read(); m=read(); s=read(); t=read(); int x,y,z; memset(head,-1,sizeof head); for(int i=1;i<=m;i++) { x=read(); y=read(); z=read(); add(x,y,z,0); add(y,x,0,0); } put(maxflow(s,t)); olinr ~~(0^_^0)+love_nmr; }
2、Dinic算法 ($普通图 O(sqrt{2E}) 二分图 O(sqrt{E}) $)
上面的网络流算法,每进行一次增广,都要做 一遍BFS,十分浪费。能否少做几次BFS? 这就是Dinic算法要解决的问题
首先:先利用BFS对残量网络分层--------一个节点的深度,就是源点到它最少要经过的边数。
分完层后,利用DFS从前一层向后一层反复寻找增广路。
要是碰到了汇点,则说明找到了一条增广路径。此时要增加总流量的值,进行增广。
优化:这种dfs的多路增广不是一次一次找路,而是一次性找一张网
对于每一个点,相当于对其进行了彻底的增广,
(即这条已经被增广过的边已经发挥出了它全部的潜力,不可能再被增广了),下一次就不必再检查它,而直接看第一个未被检查的边。
保存一下每个节点正在考虑的边cur[i],已经增广的边就不用走了
#include<cstdio> #include<iostream> #include<cstring> #include<cctype> #include<algorithm> #include<queue> using namespace std; #define int long long #define olinr return #define _ 0 #define love_nmr 0 #define DB double struct node { int nxt; int to; int flow; int cap; }edge[205050]; int head[10505]; int dis[10505]; int cur[205050]; int n; int m; int s; int t; int cnt=-1; queue<int>q; inline int read() { int x=0,f=1; char ch=getchar(); while(!isdigit(ch)) { if(ch=='-') f=-f; ch=getchar(); } while(isdigit(ch)) { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*f; } inline void put(int x) { if(x<0) { x=-x; putchar('-'); } if(x>9) put(x/10); putchar(x%10+'0'); } inline void add(int from,int to,int cap,int flow) { cnt++; edge[cnt].cap=cap; edge[cnt].to=to; edge[cnt].nxt=head[from]; edge[cnt].flow=flow; head[from]=cnt; } inline bool bfs() { for(int i=1;i<=n;i++) //初始化cur cur[i]=head[i]; memset(dis,0x7f,sizeof dis); //找增广路 while(!q.empty()) q.pop(); q.push(s); dis[s]=0; while(!q.empty()) { int tp=q.front(); q.pop(); for(int i=head[tp];i!=-1;i=edge[i].nxt) { int go=edge[i].to; if(dis[go]>1e9&&edge[i].cap>edge[i].flow) //没遍历过并且能流过去 { dis[go]=dis[tp]+1; //更新距离(层) q.push(go); } } } if(dis[t]>1e9) return false; //到不了t return true; } inline int dfs(int now,int change) { if(now==t||!change) return change; //到了终点或者无法增广(改进量为0) int flow=0,ls=0; for(int i=cur[now];i!=-1;i=edge[i].nxt) { cur[now]=i; //记录当前点所遍历的最新边,下次从它开始,避免重复 int go=edge[i].to; if((dis[go]==dis[now]+1)&&(ls=dfs(go,min(change,edge[i].cap-edge[i].flow)))) //找到这条路并且找min的change { flow+=ls; change-=ls; //改进量的限制 edge[i].flow+=ls; //增广修改 edge[i^1].flow-=ls; if(!change) break; } } return flow; } inline int maxflow() { int flow=0; while(bfs()) flow+=dfs(s,0x7fffffff); return flow; } signed main() { n=read(); m=read(); s=read(); t=read(); int x,y,z; memset(head,-1,sizeof head); for(int i=1;i<=m;i++) { x=read(); y=read(); z=read(); add(x,y,z,0); add(y,x,0,0); } put(maxflow()); olinr ~~(0^_^0)+love_nmr; }
然而还有更快的QAQ
3、Isap算法(渐进时间复杂度和dinic相同,但是非二分图的情况下isap更具优势。)
ISAP也是基于分层思想的最大流算法。
所不同的是,它省去了Dinic每次增广后需要重新构建分层图的麻烦,而是在每次增广完成后自动更新每个点的标号(也就是所在的层)
最短增广路算法是一种运用距离标号使寻找增广路的时间复杂度下降的算法。
-
-
每次沿可行边进行增广, 可行边即dis[from]=dis[go]+1
-
找到增广路后,将路径上所有边的流量更新.
-
遍历完当前结点的可行边后更新当前结点的标号为 dis[now] = min( dis[now] , dis[go])+1 (E(now,go)的cap>flow), 使下次再搜的时候有路可走。
-
图中不存在增广路后即退出程序,此时得到的流量值就是最大流。
由于可行边定义为:(now,next) | h[now] = h[next]+1,所以若标号出现“断层”即有的标号对应的顶点个数为0,则说明剩余图中不存在增广路,此时便可以直接退出,降低了无效搜索。
举个锤子:若结点标号为3的结点个数为0,而标号为4的结点和标号为2的结点都大于 0,那么在搜索至任意一个标号为4的结点时,便无法再继续往下搜索,说明图中就不存在增广路。
此时即可结束
#include<cstdio> #include<iostream> #include<cstring> #include<cctype> #include<algorithm> #include<queue> using namespace std; #define int long long #define olinr return #define _ 0 #define love_nmr 0 #define DB double struct node { int flow; int cap; int nxt; int to; }edge[205050]; int head[10505]; int cur[10505]; int cnt=-1; int dis[10505]; int tong[10505]; int lst[10505]; int n; int m; int s; int t; int maxflow; queue<int> q; inline int read() { int x=0,f=1; char ch=getchar(); while(!isdigit(ch)) { if(ch=='-') f=-f; ch=getchar(); } while(isdigit(ch)) { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*f; } inline void put(int x) { if(x<0) { x=-x; putchar('-'); } if(x>9) put(x/10); putchar(x%10+'0'); } inline void add(int from,int to,int cap,int flow) { cnt++; edge[cnt].to=to; edge[cnt].nxt=head[from]; edge[cnt].flow=flow; edge[cnt].cap=cap; head[from]=cnt; } inline void bfs() { q.push(t); for(int i=1;i<=n;i++) dis[i]=n; dis[t]=0; while(!q.empty()) { int tp=q.front(); q.pop(); for(int i=head[tp];i;i=edge[i].nxt) { int go=edge[i].to; if(dis[go]==n&&edge[i^1].cap>edge[i^1].flow) //反向找求dis { dis[go]=dis[tp]+1; q.push(go); } } } } inline int add_flow() { int change=0x7ffffff; //改变量为路径最小残量 int now=t; while(now!=s) { change=min(change,edge[lst[now]].cap-edge[lst[now]].flow); //找最小残量 now=edge[lst[now]^1].to; //往回跳 } now=t; while(now!=s) { edge[lst[now]].flow+=change; //改变流量 edge[lst[now]^1].flow-=change; now=edge[lst[now]^1].to; } return change; } inline void isap() { for(int i=1;i<=n;i++) cur[i]=head[i]; //同DINIC int now=s; for(int i=1;i<=n;i++) tong[dis[i]]++; //开桶,记录当前合法路径的点的深度,优化断层情况 while(dis[s]<n) { if(now==t) { maxflow+=add_flow(); //最大流+ now=s; //再从s跑增广路 } bool flag=0; for(int i=cur[now];i!=-1;i=edge[i].nxt) { int go=edge[i].to; if(dis[now]==dis[go]+1&&edge[i].cap>edge[i].flow) { flag=true; lst[go]=i; cur[now]=i; //找到能增广的边就行,不用管是哪条 now=go; break; //找到就break继续 } } if(!flag) //当前点此时从cur开始的边都无法增广 { int minn=n-1; for(int i=head[now];i!=-1;i=edge[i].nxt) { int go=edge[i].to; if(edge[i].cap>edge[i].flow) minn=min(minn,dis[go]); //重新编号,找最小的+1 } tong[dis[now]]--; //改变编号 if(!tong[dis[now]]) break; //断层!!!!! dis[now]=minn+1; //重新编号 tong[dis[now]]++; cur[now]=head[now]; //更新 if(now!=s) now=edge[lst[now]^1].to; //当前点处理完,往回跳 } } } signed main() { n=read(); m=read(); s=read(); t=read(); int x,y,z; memset(head,-1,sizeof head); for(int i=1;i<=m;i++) { x=read(); y=read(); z=read(); add(x,y,z,0); add(y,x,0,0); } isap(); put(maxflow); olinr ~~(0^_^0)+love_nmr; }
透彻~~~~~