对于已经得到的样本集,核密度估计是一种可以求得样本的分布的概率密度函数的方法:
通过选取核函数和合适的带宽,可以得到样本的distribution probability,在这里核函数选取标准正态分布函数,bandwidth通过AMISE规则选取
具体原理及定义:传送门 https://en.wikipedia.org/wiki/Density_estimation
MATLAB 代码实现如下:
% Kernel Density Estimation
% 只能处理正半轴密度
function [t, y_true, tt, y_KDE] = KernelDensityEstimation(x)
% clear
% x = px_last;
% x = px_last_tu;
%%
%参数初始化
Max = round(max(x)); %数据中最大值
Min = round(min(x)); %数据中最小值
Ntotal = length(x); %数据个数
tt = 0 : 0.1 : Max; %精确x轴
t = 0 : Max; %粗略x轴
y_KDE = zeros(10 * Max+1, 1); %核密度估计值
sum1 = 0; %求和的中间变量
%%
%计算带宽h
R = 1/(2*sqrt(pi));
m2 = 1;
h = 3;
% h = (R)^(1/5) / (m2^(2/5) * R^(1/5) * Ntotal^(1/5));
%%
%计算核密度估计
for i = 0 : 0.1 : Max
for j = 1 : Ntotal
sum1 = sum1 + normpdf(i-x(j));
end
y_KDE(round(i*10+1)) = sum1 / (h * Ntotal);
sum1 = 0;
end
sum2 = sum(y_KDE)*0.1; %归一化KDE密度
for i = 0 : 0.1 : Max
y_KDE(round(i*10+1)) = y_KDE(round(i*10+1))/sum2;
end
%%
%计算真实密度的分布
y_true = zeros(Max+1,1);
for i = 0 : Max
for j = 1 : Ntotal
if (x(j) < i+1)&&(x(j) >= i)
y_true(i+1) = y_true(i+1) + 1;
end
end
y_true(i+1) = y_true(i+1) / Ntotal;
end
%%
%绘图
% figure(1) %真实密度的分布图象
% bar(t, y_true);
% axis([Min Max+1 0 max(y_true)*1.1]);
%
% figure(2) %核密度估计的密度分布图象
% plot(tt, y_KDE);
% axis([Min Max 0 max(y_true)*1.1]);
给定测试数据:
data = [1,2,3,4,5,2,1,2,4,2,1,4,7,4,1,2,4,9,8,7,10,1,2,3,1,0,0,3,6,7,8,9,4]
样本的条形统计图和KDE密度分布图分别如下,可以看到KDE可以较好的还原样本的分布情况:
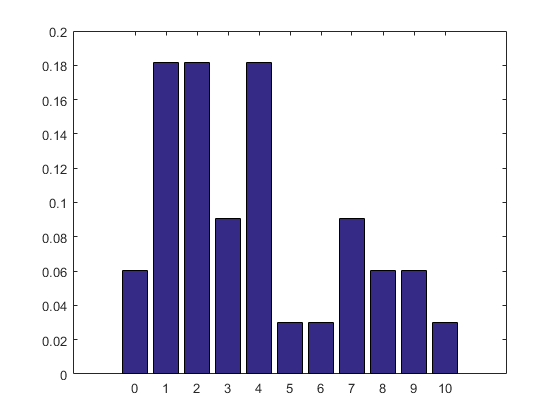
真实概率分布图
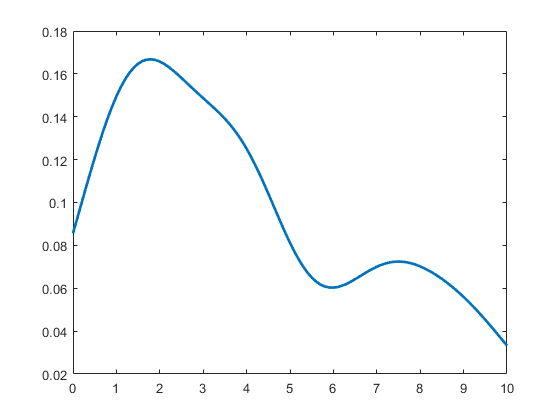
KDE密度分布图