回归 Regression ,可以理解为倒推,由结果推测出原因。
线性回归 是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,表达形式为:
y= ax+b+e
e为误差服从均值为0的正态分布。


通过已有的大量数据,x和y的值,计算得到表达式y=ax+b+e的关系,表达这种关系。
然后通过x值,可推断出y的值。

拟合:把平面上一系列的点用一条光滑的曲线链接起来的过程;
利用最小二乘法来进行曲线拟合,残差平方和,如下图;

最小二乘法
我们以最简单的一元线性模型来解释最小二乘法。什么是一元线性模型呢? 监督学习中,如果预测的变量是离散的,我们称其为分类(如决策树,支持向量机等),如果预测的变量是连续的,我们称其为回归。回归分析中,如果只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。对于二维空间线性是一条直线;对于三维空间线性是一个平面,对于多维空间线性是一个超平面...
对于一元线性回归模型, 假设从总体中获取了n组观察值(X1,Y1),(X2,Y2), …,(Xn,Yn)。对于平面中的这n个点,可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看,这条直线处于样本数据的中心位置最合理。 选择最佳拟合曲线的标准可以确定为:使总的拟合误差(即总残差)达到最小。有以下三个标准可以选择:
(1)用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。
(2)用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。
(3)最小二乘法的原则是以“残差平方和最小”确定直线位置。用最小二乘法除了计算比较方便外,得到的估计量还具有优良特性。这种方法对异常值非常敏感。
最常用的是普通最小二乘法( Ordinary Least Square,OLS):所选择的回归模型应该使所有观察值的残差平方和达到最小。(Q为残差平方和)- 即采用平方损失函数。
参考:http://blog.csdn.net/qll125596718/article/details/8248249
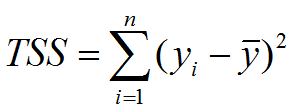
ESS: Explained Sum of Squares 回归平方和/解释平方和
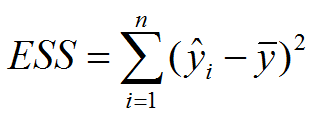
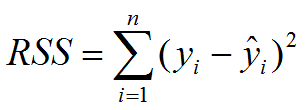
最小二乘法与梯度下降法
最小二乘法跟梯度下降法都是通过求导来求损失函数的最小值,那它们有什么区别呢。
相同
1.本质相同:两种方法都是在给定已知数据(independent & dependent variables)的前提下对dependent variables算出出一个一般性的估值函数。然后对给定新数据的dependent variables进行估算。
2.目标相同:都是在已知数据的框架内,使得估算值与实际值的总平方差尽量更小(事实上未必一定要使用平方)
不同
1.实现方法和结果不同:最小二乘法是直接对求导找出全局最小,是非迭代法。而梯度下降法是一种迭代法,先给定一个,然后向下降最快的方向调整,在若干次迭代之后找到局部最小。梯度下降法的缺点是到最小点的时候收敛速度变慢,并且对初始点的选择极为敏感,其改进大多是在这两方面下功夫。
过拟合
我们通过对数据样本的观察和抽象,最后归纳得到一个完整的数据映射模型。但是在归纳的过程中,可能为了迎合所有样本向量点甚至是噪声点而使得模型描述过于复杂。
过拟合的危害有以下几点:
1.描述复杂 模型的描述非常复杂--参数繁多,计算逻辑多。
2.失去泛华能力 所谓泛华能力就是通过机器学习得到的模型对未知数据的预测能力,即应用于其他非训练样本的向量时的分类能力。
造成过拟合的原因:
1.训练样本太少 训练样本少,训练出来的模型非常不准确
2.追求完美 对于所有的训练样本向量点都希望用拟合的模型覆盖,但在实际的训练样本中却存在很多噪声。
欠拟合
与过拟合相反,叫做欠拟合。建模不当产生的误差,主要是对线性回归中的因素考虑不足。
原因如下:
1.参数过少 对于训练样本向量的维度提取太少导致训练描述的不准确。
2.拟合不当 通常是拟合方法的不正确
非线性回归的情况太过复杂,在生产实践中也尽量避免使用这种模型。多采取线性回归
例子
数据文件内容:
29,female,27.94,1,yes,southeast,19107.7796 49,female,27.17,0,no,southeast,8601.3293 37,female,23.37,2,no,northwest,6686.4313 44,male,37.1,2,no,southwest,7740.337 18,male,23.75,0,no,northeast,1705.6245 20,female,28.975,0,no,northwest,2257.47525 44,male,31.35,1,yes,northeast,39556.4945 47,female,33.915,3,no,northwest,10115.00885 26,female,28.785,0,no,northeast,3385.39915 19,female,28.3,0,yes,southwest,17081.08 52,female,37.4,0,no,southwest,9634.538 32,female,17.765,2,yes,northwest,32734.1863 38,male,34.7,2,no,southwest,6082.405 59,female,26.505,0,no,northeast,12815.44495 61,female,22.04,0,no,northeast,13616.3586 53,female,35.9,2,no,southwest,11163.568 19,male,25.555,0,no,northwest,1632.56445 20,female,28.785,0,no,northeast,2457.21115 22,female,28.05,0,no,southeast,2155.6815 19,male,34.1,0,no,southwest,1261.442 22,male,25.175,0,no,northwest,2045.68525 54,female,31.9,3,no,southeast,27322.73386 22,female,36,0,no,southwest,2166.732 34,male,22.42,2,no,northeast,27375.90478 26,male,32.49,1,no,northeast,3490.5491 34,male,25.3,2,yes,southeast,18972.495 29,male,29.735,2,no,northwest,18157.876
......
执行过程分析:
> insurance <- read.csv("insurance.csv", stringsAsFactors = TRUE) #读取数据 > str(insurance) #查看data.frame结构 'data.frame': 1338 obs. of 7 variables: $ age : int 19 18 28 33 32 31 46 37 37 60 ... $ sex : Factor w/ 2 levels "female","male": 1 2 2 2 2 1 1 1 2 1 ... $ bmi : num 27.9 33.8 33 22.7 28.9 ... $ children: int 0 1 3 0 0 0 1 3 2 0 ... $ smoker : Factor w/ 2 levels "no","yes": 2 1 1 1 1 1 1 1 1 1 ... $ region : Factor w/ 4 levels "northeast","northwest",..: 4 3 3 2 2 3 3 2 1 2 ... $ charges : num 16885 1726 4449 21984 3867 ...> library("psych") #加载包 > ins_model <- lm(charges ~ age + children + bmi + sex + smoker + region, data=insurance) #使用包的线性回归方法训练数据集 > summary(ins_model) #查看训练集汇总信息 Call: lm(formula = charges ~ age + children + bmi + sex + smoker + region, data = insurance) Residuals: Min 1Q Median 3Q Max -11304.9 -2848.1 -982.1 1393.9 29992.8 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -11938.5 987.8 -12.086 < 2e-16 *** age 256.9 11.9 21.587 < 2e-16 *** #*多代表显著特征 children 475.5 137.8 3.451 0.000577 *** bmi 339.2 28.6 11.860 < 2e-16 *** sexmale -131.3 332.9 -0.394 0.693348 smokeryes 23848.5 413.1 57.723 < 2e-16 *** regionnorthwest -353.0 476.3 -0.741 0.458769 regionsoutheast -1035.0 478.7 -2.162 0.030782 * regionsouthwest -960.0 477.9 -2.009 0.044765 * --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 6062 on 1329 degrees of freedom Multiple R-squared: 0.7509, Adjusted R-squared: 0.7494 F-statistic: 500.8 on 8 and 1329 DF, p-value: < 2.2e-16 > lmstep<- step(ins_model) #用于去除不显著的特征 Start: AIC=23316.43 charges ~ age + children + bmi + sex + smoker + region Df Sum of Sq RSS AIC - sex 1 5.7164e+06 4.8845e+10 23315 #sex特征被删除 <none> 4.8840e+10 23316 - region 3 2.3343e+08 4.9073e+10 23317 - children 1 4.3755e+08 4.9277e+10 23326 - bmi 1 5.1692e+09 5.4009e+10 23449 - age 1 1.7124e+10 6.5964e+10 23717 - smoker 1 1.2245e+11 1.7129e+11 24993 Step: AIC=23314.58 #用AIC最小值来评估 charges ~ age + children + bmi + smoker + region Df Sum of Sq RSS AIC <none> 4.8845e+10 23315 - region 3 2.3320e+08 4.9078e+10 23315 - children 1 4.3596e+08 4.9281e+10 23325 - bmi 1 5.1645e+09 5.4010e+10 23447 - age 1 1.7151e+10 6.5996e+10 23715 - smoker 1 1.2301e+11 1.7186e+11 24996 > predict.lm(lmstep,data.frame(age=70,children=4,bmi=31.5,smoker='yes',region='northeast'),interval="prediction",level=0.95) #使用预测方法对数据进行预测 fit lwr upr 1 42400.38 30429.87 54370.89 #预测结果 42400.38 置信区间 30429.87~54370.89
查看图:
> plot(lmstep)

X轴预测值,Y轴残值;反映预测值和真实值的距离;异常值 243、1301、578

QQ图 X理论分为区间;Y标准化残差值 判断是否符合正态分布, 粗略判断大于2及小于-2的点为离群点

X轴预测值,Y轴标准化残差值开方

X轴杠杆比率,Y轴标准化残差值 leverage=d(预测值)/ d(真实值)