牛顿法用到了目标函数的1、2阶导数,可能会更高效。
1.思想:构造目标函数的近似函数:

1.2泰勒展开到二阶,可以得到函数f(x)的近似函数:
![]()
1.3对近似函数q(x)求极小值,得到迭代形式:
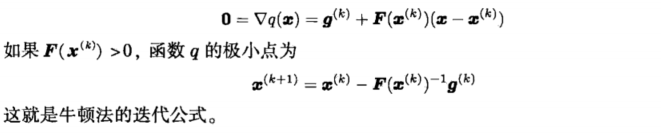
1.4流程:
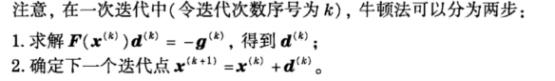
2.二次型中牛顿法
二次型中,牛顿法只需一次迭代即可从任意初始点x(0)收敛到f的极小的x*,满足在x*的梯度=0。

问题,有时候随机初始点离极小/大点较远时,并不一定收敛,有时候黑塞矩阵为奇异矩阵,则完全无法使用了,有一些修正方法。
1)开展一次一维搜索:
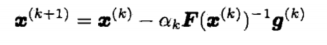

问题是这种方法在维数n太大时,计算黑塞矩阵计算量太大,还需要解F(x(k))-1,得到方向d,这是牛顿法的重要缺陷之一。(后续10、11章的共轭方法、拟牛顿法可以避免求黑塞矩阵的逆以解决这一问题)
2)Levenberg-Marquardt修正
加入uk倍单位矩阵,使得修正后的矩阵G总保存正定,加入ak,开展一维搜索:

3. 牛顿法拟合非线性最小二乘函数:9.4