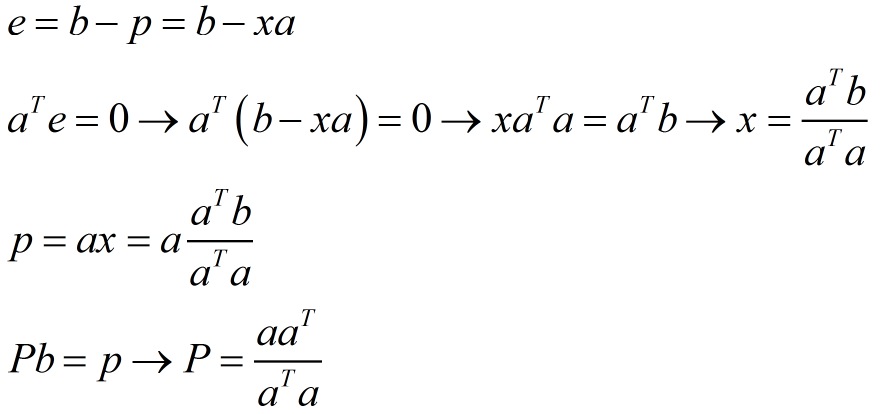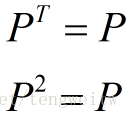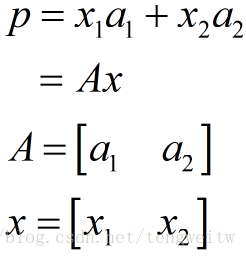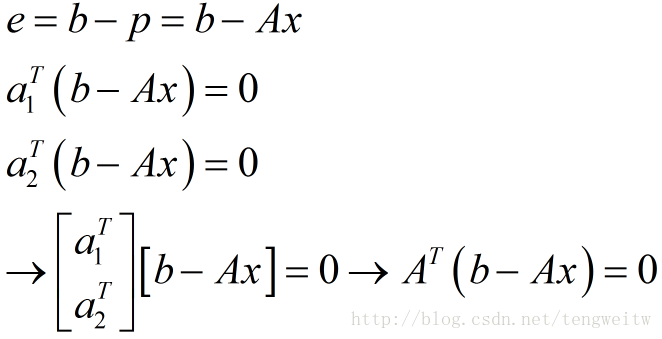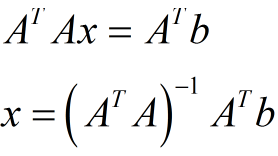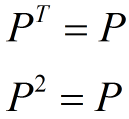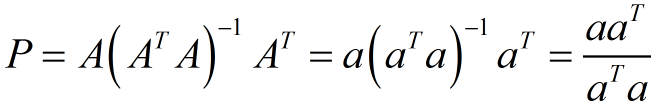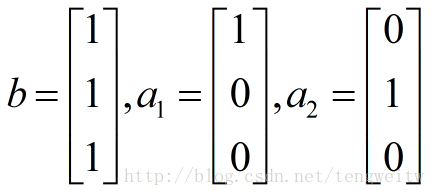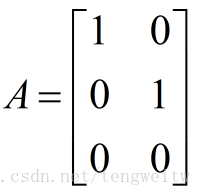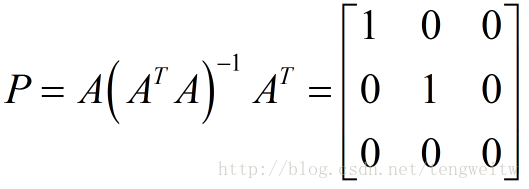来自:https://blog.csdn.net/tengweitw/article/details/41174555
二维投影
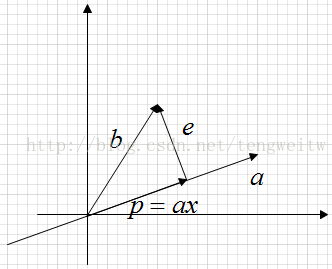
上图表示的是,向量b在向量a上的投影。显然有例如以下表达式:
当中,P为投影矩阵,由P的表达式能够看出,它具有例如以下性质:
三维投影
三维投影,就是将一个向量投影到一个平面上。同上面一样,如果是将b向量投影到平面上的p向量,则有表达式:
e是垂直与平面的向量。
因为p向量在平面上。则p向量能够由该平面的2个线性无关向量(正如。在xy平面的不论什么向量都能够由x轴,y轴表示)表示:
因为e垂直平面,则e向量垂直与平面中的随意向量。则有:
将上式化简求得x:
又由于p=Ax,Pb=p,则得到投影矩阵为:
由P的表达式能够看出,它具有例如以下性质:
上面的投影矩阵是通式。当投影在一维情况时,数值的逆是它的倒数,A即为直线上的随意一个向量a,投影矩阵为:
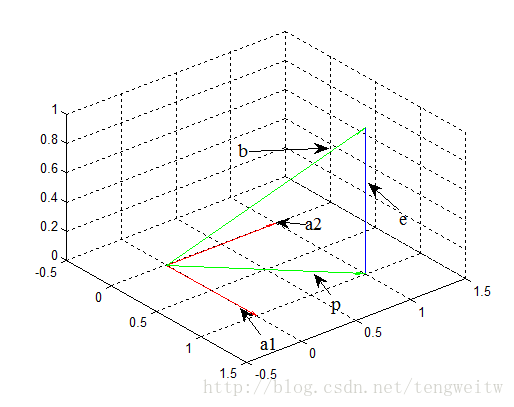
实例说明:
如上图,如果我们要将向量b投影到水平面上。其投影为p,a1,a2为水平面的两个线性无关向量,它们的參数分别为:
那么A=[a1 a2]即:
由上面我们求得的通式,可得投影矩阵P:
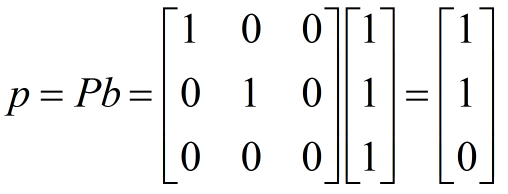
知道投影矩阵P后。我们能够得到b在水平面上的投影p为:
显然,p与我们图中所看到的的结果同样。这里我们是以三维情况进行举例的,更高维情况。我们无法用图像来描写叙述,可是通式也是成立的。