典型问题－－连通性

１．问题示例

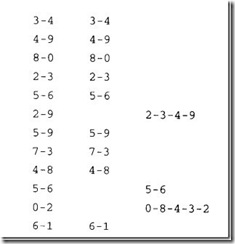
如果新输入的对，可以由以前的输入对连通，就不会输出；如果不能由以前的对连通，就输出这个对。例如2-9不在输出之列，因为前面的对存在2-3-4-9的连通。

２．算法实现

抽象操作：

·查找已有的数据项集合

·将结果合并到数据项集合中

２.１ 快速查找算法

#include <stdio.h>
#define N 10000
void main()
{
    int i, p, q, t, id[N];
    for(i = 0; i < N; i++)
        id[i] = i;
    while (scanf("%d-%d\n", &p, &q) == 2)
    {
        if(id[p] == id[q])
            continue;

        //遍历数组，把所有值等于id[q]的元素的值改为id[p]。
        for(t = id[p], i = 0; i < N; i++)
            if(id[i] == t)
                id[i] = id[q];
        printf(" %d-%d\n", p, q);
    }
}

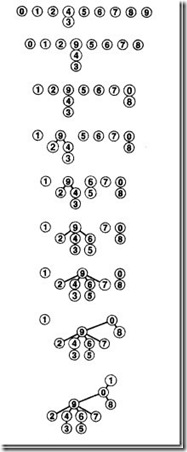
          图2-1 快速查找示例(慢速合并)

当id[p] = id[q]时，表示p和q连通。

２.２  快速合并算法

#include <stdio.h>
#define N 10000
main()
{
    int i, j, p, q, id[N];
    for(i = 0; i < N; i++)
        id[i] = i;
    while (scanf("%d-%d\n", &p, &q) == 2)
    {
        for(i = p; i != id[i]; i = id[i]) ;   //查找p所在树1的根节点
        for(j = q; j != id[j]; j = id[j]) ;   //查找q所在树2的根节点 
        if(i == j)
            continue;
        id[i] = j;   //树2连入树1

        printf(" %d-%d\n", p, q);
    }
}

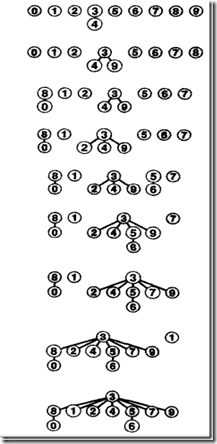
      图2-2 快速合并算法示例（不是太快的查找）

２.３ 加权快速合并算法

利用数组sz[N]记录了树的节点数，保证每次合并时将较小的树根连到较大的树根上面，避免产生太深的树，减少查找遍历次数。

#include <stdio.h>
#define N 10000
void main()
{
    int i, j, p, q, id[N], sz[N];
    for(i = 0; i < N; i++)
    {
        id[i] = i;
        sz[i] = 1;
    }
    while (scanf("%d-%d\n", &p, &q) == 2)
    {
        for(i = p; i != id[i]; i = id[i]) ;
        for(j = q; j != id[j]; j = id[j]) ;
        if(i == j)
            continue;
        if(sz[i] < sz[j])
        {
            id[i] = j;
            sz[j] += sz[i];
        }
        else
        {
            id[j] = i;
            sz[i] += sz[j];
        }
        printf(" %d %d\n", p, q);
    }
}

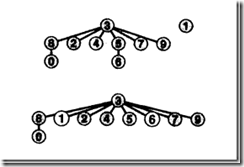
　图2-3 加权快速合并算法的树型表示

这颗树中每个节点到根节点的距离变小，因而查找更高效。

２.３ 等分路径压缩

代替2.2中的for循环，通过使每条链接跳跃到树中向上的路径的下一个节点实现压缩。

for(i = p; i != id[i]; i = id[i]) 
    id[i] = id[id[i]];
for(j = q; j != id[j]; j = id[j]) 
    id[j] = id[id[j]];

　　图2-3  等分路径压缩

当处理1和6的时候，让1、5、6都指向3，得到的树比上面的算法更扁平。

２.４ 完全路径压缩

在合并操作的过程中，添加经过每条路径的另一个指针，使沿路遇见的每个顶点对应的id元素指向树的根节点。

#include <stdio.h>
#include <stdlib.h>
#define BUFFER_MAX_SIZE 16
int main(int argc, char *argv[]) 
{
    int con[BUFFER_MAX_SIZE];
    int con_cnt[BUFFER_MAX_SIZE];
    int elem[BUFFER_MAX_SIZE][BUFFER_MAX_SIZE];
    int elem_cnt[BUFFER_MAX_SIZE];
    int p, q, r, i, j, k;
    for(r=0; r<BUFFER_MAX_SIZE; r++) 
    {
        con[r]=r;
        con_cnt[r]=1;
        elem[r][0]=r;
        elem_cnt[r]=1;
    }
    
    while(scanf("%d-%d", &p, &q)==2) 
    {
        if(p>=BUFFER_MAX_SIZE||q>=BUFFER_MAX_SIZE)
            exit(EXIT_FAILURE);
        for(i=p; i!=con[i]; i=con[i]);
        for(j=q; j!=con[j]; j=con[j]);
        if(i==j)
            continue;
        if(con_cnt[i]<con_cnt[j]) 
        {
            k=elem_cnt[j];
            for(r=0; r<elem_cnt[i]; r++)
                elem[j][elem_cnt[j]++]=elem[i][r];
            for(r=k; r<elem_cnt[j]; r++)
                con[elem[j][r]]=j;
            con_cnt[j]+=con_cnt[i];
        }
        else 
        {
            k=elem_cnt[i];
            for(r=0; r<elem_cnt[j]; r++)
                elem[i][elem_cnt[i]++]=elem[j][r];
            for(r=k; r<elem_cnt[i]; r++)
                con[elem[i][r]]=i;
            con_cnt[i]+=con_cnt[j];
        }
        printf("%d-%d\n", p, q);
        for(r=0; r<BUFFER_MAX_SIZE; r++)
            printf("%d\t", con[r]);
        printf("\n");
    }
    exit(EXIT_SUCCESS);
}