最大子段和
例题:http://acm.sdut.edu.cn/onlinejudge2/index.php/Home/Contest/contestproblem/cid/3015/pid/3664
题目解析:最大子段和,从三种角度来解决。
算法一:分治算法
算法思路:
1. 我们先来考虑一下如何求 [2,-1,2] / [2,-4,3] 这两个的最大子段。
第一个的最大子段,是 2+(-1)+2;第二个的最大子段是 3。
2. 分治算法处理:
我们把一个大问题分为很多小问题,而大化小最好的办法是二分法。
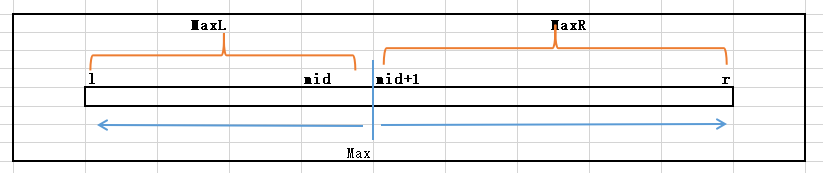
看上图,我们一共求三块,前两块(MaxL,MaxR)是递归求解出来的真正的左边最大子段,右边最大子段;而Max是判断这两个子段是否能合并在一起。
如果能合并在一起,则Max=MaxL+MaxR,否则是独立的。
你应该明确一个前提,左边最大,右边最大,连接起来并不一定最大,举个极端的例子 [ 1,-1,-1,-1,-1,-1,1]。如果否定前提,则这个子段最大和应该为2,但显然是错误的。
实际上:左边最大,右边最大,则它们和可能更小,可能更大,也可能一样;其取决于连接在一起之后的结果。
解决方案:从[l <-- mid],试探性相加,每次相加判断是否满足最大,如果是则记录,直到最后则求出的肯定是"从mid开始到l的最大子段"(并非最大子段,是从mid开始,因为要连接在一起连接口必须在mid),右边同理。
左右都计算出来结果为Max,然后分别与MaxR与MaxL比较(并非MaxR+MaxL,因为我们之前强调过这个思想是错误的)。
源代码:
1 // 算法.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。 2 // 3 4 #include "pch.h" 5 #include <iostream> 6 #include <map> 7 #include <math.h> 8 #include <algorithm> 9 using namespace std; 10 11 int a[100000]; 12 int cnt; 13 14 int MaxSegment(int l,int r){ 15 cnt++; 16 int sum = 0; 17 if (l == r) { 18 if (a[l] >= 0)sum = a[l]; 19 else sum = 0; 20 } 21 else { 22 int mid = (l + r)/ 2; 23 int MaxL = MaxSegment(l, mid); 24 int MaxR = MaxSegment(mid+1, r); 25 int s1 = 0,s2=0, ss = 0; 26 // 开始向左计算 27 for (int i = mid; i >=l;i-- ) { 28 ss += a[i]; 29 if (ss > s1)s1 = ss; 30 } 31 32 // 开始向右计算 33 ss = 0; 34 for (int i = mid + 1; i <= r; i++) { 35 ss += a[i]; 36 if (ss > s2)s2 = ss; 37 } 38 39 sum = s1 + s2; 40 sum = max(sum, MaxL); 41 sum = max(sum, MaxR); 42 } 43 return sum; 44 } 45 int main() { 46 int n; 47 cin >> n; 48 for (int i = 0; i < n; i++) 49 scanf_s("%d",&a[i]); 50 int Max = MaxSegment(0, n - 1); 51 printf("%d %d", Max, cnt); 52 }
算法二:递推法