[动态规划]石子合并问题

https://acm.sdut.edu.cn/onlinejudge2/index.php/Home/Contest/contestproblem/cid/3016/pid/1729

石子合并问题

Time Limit: 1000 ms Memory Limit: 65536 KiB

 

Problem Description

在一个圆形操场的四周摆放着n堆石子。现要将石子有次序地合并成一堆。规定每次只能选相邻的2 堆石子合并成新的一堆，并将新的一堆石子数记为该次合并的得分。试设计一个算法，计算出将n堆石子合并成一堆的最小得分和最大得分。
对于给定n堆石子,计算合并成一堆的最小得分和最大得分。

Input

输入数据的第1行是正整数n，1≤n≤100，表示有n堆石子。第二行有n个数，分别表示每堆石子的个数。

Output

输出数据有两行，第1行中的数是最小得分，第2行中的数是最大得分。

Sample Input

4
4 4 5 9

Sample Output

43
54

---

算法考试考完了(题目有点简单侥幸AK..),但这个问题当时困扰我了很久，网上解答的很模糊，因此还是在这里记录一下吧。

这题的难点是：如果将环形转换为直线（直线的网上有很多解答，这里不做赘述）。

其核心思想就是：通过将数量变为 2n-1 来转换成直线问题。

当时看到这几行字困惑了很久，一直不太理解，但之后画图就懂了。

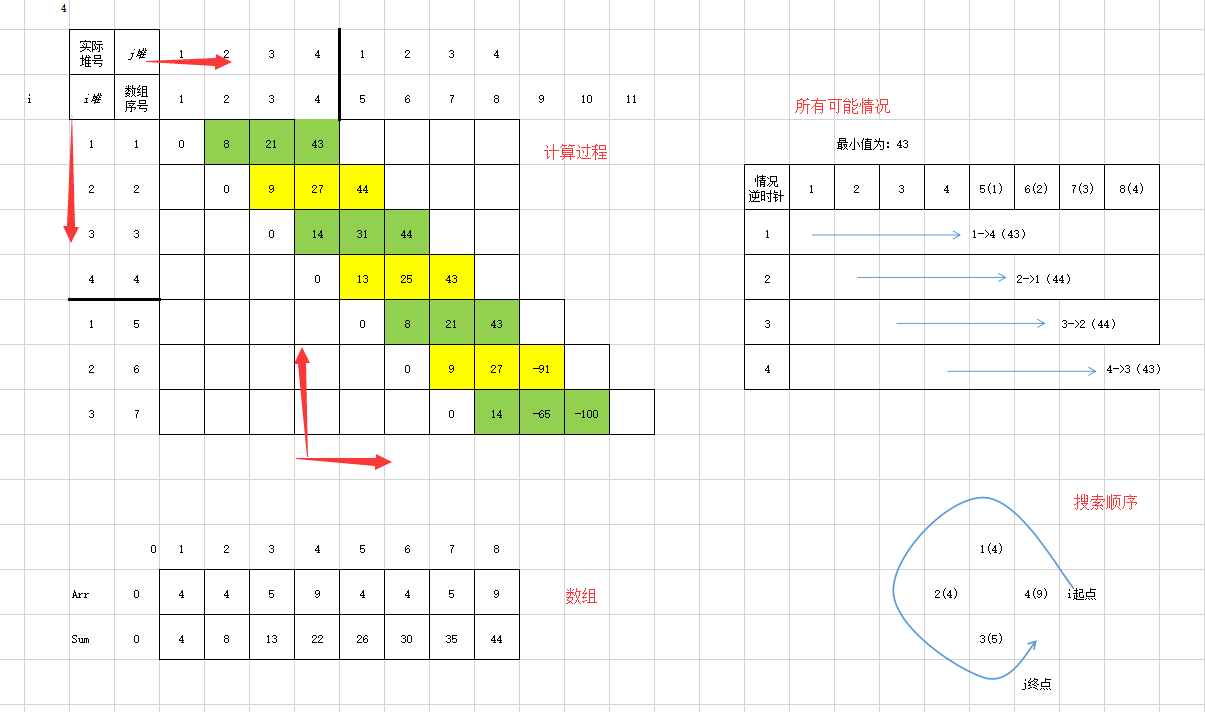
1. 我们为了将环形变为直线，必须规定转动顺序，这里采用逆时针转动，且以 i 作为起点，j作为终点。(右下图）

2. 当规定好终点了，那么这环形有4种情况，我们求在这四种情况下最下的。(右上图）

3. 关于转换成直线，比如存在 a(0) -> b(1) -> c(2) -> d(3) 与 d(3) -> a(4) -> b(5) -> c(6)。

　　第一条是 i=0,j=3的数组，第二条是 i=3,j=6 的数组。 这样，我们就不用返回去计算了( 3->0->1->2 ???)。

4. 四种情况分别是数组中的四行，每行最后一个代表遍历的结果，我们最后只需要遍历这四个值，找到最小值即可。

---

源代码：

#include <iostream>
#include <stdio.h>
#include <algorithm>
#define INF 0x3f3f3f3f
using namespace std;
int Arr[300],Sum[300];
int Min[300][300], Max[300][300];
int main() {
    int n;
    cin >> n;

    // 初始化数组
    for (int i = 1; i <= n; i++) {
        cin >> Arr[i];
        Arr[i + n] = Arr[i];
    }

    // 计算最大和
    for (int i = 1; i <= 2 * n; i++) {
        Sum[i] = Sum[i - 1] + Arr[i];
    }

    // 开始递归循环
    for (int i = 2 * n-1; i >= 1; i--) {
        for (int j = i + 1; j < i + n; j++) {
            Min[i][j] = INF;
            for (int k = i; k < j; k++) {
                Min[i][j] = min(Min[i][j], Min[i][k] + Min[k + 1][j] + Sum[j] - Sum[i - 1]);
                Max[i][j] = max(Max[i][j], Max[i][k] + Max[k + 1][j] + Sum[j] - Sum[i - 1]);
            }
        }
    }

    // 遍历找到最大与最小值
    int MaxValue = 0, MinValue = INF;
    for (int i = 1; i <= n; i++) {
        MaxValue = max(MaxValue, Max[i][i + n - 1]);
        MinValue = min(MinValue, Min[i][i + n - 1]);
    }

    cout << MinValue << endl << MaxValue << endl;

}