【BZOJ】2705: [SDOI2012]Longge的问题

【题意】给定n，求∑gcd(i,n),(1<=i<=n)，n<=2^32

【算法】数论（欧拉函数，gcd）

【题解】批量求gcd的题目常常可以反过来枚举gcd的值。

记f(g)为gcd(i,n)=g的i的个数，则有ans=∑f(g)*g，g|n。

gcd(i,n)=g即gcd(i/g,n/g)=1，f(g)转化为φ(n/g)。

所以，ans=∑g*φ(n/g)，g|n。

当然，这种纯数论问题也可以用公式法直接求解。

引用自：clover_hxy

gcd分解：d|gcd(a,b)=d|a&&d|b

过程中，[d|i]表示d是否整除i。

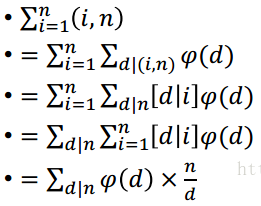
(图片来源：clover_hxy）

解释：第一步，用公式∑_d|nφ(d)=n转化出欧拉函数。第二步，分解gcd，d|gcd(i,n)=d|i&&d|n，选择枚举d|n并依次判断d|i是否成立。

第三步，交换顺序。第四步，对于每个d，1~n中能被d整除的数字个数为n/d，得到ans=φ(d)*n/d，d|n。这个公式和之前的一致。

具体实现：

1.枚举1~sqrt(n)寻找n的因数

2.枚举2~sqrt(n)寻找n的素因数，n每次除尽已枚举到的质因数，最后x>1则x是大质数。

#include<cstdio>
#include<algorithm>
#define ll long long
using namespace std;
ll n,ans;
ll phi(ll x){
    ll num=x;
    for(ll i=2;i*i<=x;i++)if(x%i==0){
        num=num*(i-1)/i;
        while(x%i==0)x/=i;
    }
    if(x>1)num=num*(x-1)/x;
    return num;
}
int main(){
    scanf("%lld",&n);
    ans=0;
    for(ll i=1;i*i<=n;i++)if(n%i==0){
        ans+=phi(n/i)*i;
        if(i*i!=n)ans+=phi(i)*n/i;
    }
    printf("%lld",ans);
    return 0;
}