最大流练习

伊基的故事 I - 道路重建

求关键边的数量
跑一遍最大流，在残留网络中，预处理出源点可以到达的点和可以到达汇点的点
枚举每一条满流的边，如果它的起点可以从源点到达，终点可以到达汇点，则该边是关键边
注：预处理可到汇点的点的时候，可以沿着残留网络的反向边走，但判断是否能走要用正向边容量

#include <bits/stdc++.h>
using namespace std;

const int N = 500 + 10;
const int M = (5000 + 10) * 2;
const int INF = 1e9;

int n, m, S, T;
struct Edge
{
	int to, nxt, flow;	
}line[M];
int fist[N], idx;
int cur[N], d[N];
bool vis_s[N], vis_t[N];

void add(int x, int y, int z)
{
	line[idx] = {y, fist[x], z};
	fist[x] = idx ++;
	line[idx] = {x, fist[y], 0};
	fist[y] = idx ++;
}

bool bfs()
{
	queue<int> q;
	memset(d, -1, sizeof d);
	q.push(S), d[S] = 0, cur[S] = fist[S];
	while(!q.empty()) 
	{
		int u = q.front(); q.pop();
		for(int i = fist[u]; i != -1; i = line[i].nxt)
		{
			int v = line[i].to;
			if(d[v] == -1 && line[i].flow)
			{
				d[v] = d[u] + 1;
				cur[v] = fist[v];
				if(v == T) return 1;
				q.push(v);
			}
		}
	}
	return 0;
}

int find(int u, int limit)
{
	if(u == T) return limit;
	int flow = 0;
	for(int i = cur[u]; i != -1 && flow < limit; i = line[i].nxt)
	{
		cur[u] = i; 
		int v = line[i].to;
		if(d[v] == d[u] + 1 && line[i].flow)
		{
			int t = find(v, min(line[i].flow, limit - flow));
			if(!t) d[v] = -1;
			line[i].flow -= t;
			line[i ^ 1].flow += t;
			flow += t;
		} 
	}	
	return flow;
}

int dinic()
{
	int res = 0, flow;
	while(bfs()) while(flow = find(S, INF)) res += flow;
	return res;
}

void dfs(int u, bool st[], int t)
{
	st[u] = 1;
	for(int i = fist[u]; i != -1; i = line[i].nxt)
	{
		int v = line[i].to;
		if(line[i ^ t].flow && !st[v])
			dfs(v, st, t);
	}
}

int main()
{
	scanf("%d%d", &n, &m);
	S = 0, T = n - 1;
	memset(fist, -1, sizeof fist); 
	for(int i = 1; i <= m; ++ i)
	{
		int a, b, c;
		scanf("%d%d%d", &a, &b, &c);
		add(a, b, c);
	}
	dinic();
	dfs(S, vis_s, 0);
	dfs(T, vis_t, 1);
	
	int res = 0;
	for(int i = 0; i < idx; i += 2)
	{
		int u = line[i ^ 1].to, v = line[i].to;
		if(!line[i].flow && vis_s[u] && vis_t[v]) ++ res;
	}
	printf("%d
", res);
	return 0;
}

秘密挤奶机

(N) 个点， (P) 条边的无向图，从 (1) 到 (N) 完成 (T) 次行程，每条边只能走一次
求 (T) 条路径中必须使用的最长的边的最小可能值

最大流判定
二分答案，判定是否可以只用不超过答案长度的边满足题意
按照原图建双向边，容量都是 (1)，若正向边反向边都流一次，等价于不流
对于两个点之间，没有必要建 (4) 条边，可以将相同的边容量合并
从 (1) 到 (n) 的最大流就是路径的数量， 判断是否满足题意即可

#include <bits/stdc++.h>
using namespace std;

const int N = 200 + 10;
const int M = (40000 + 10) * 2;
const int INF = 1e9;

int n, m, k, S, T;
struct Edge
{
	int to, nxt, flow, w;
}line[M];
int fist[N], idx;
int cur[N], d[N];

void add(int x, int y, int z)
{
	line[idx] = {y, fist[x], 0, z};
	fist[x] = idx ++;
	line[idx] = {x, fist[y], 0, z};
	fist[y] = idx ++;	
}

bool bfs()
{
	queue<int> q;
	memset(d, -1, sizeof d);
	q.push(S), d[S] = 0, cur[S] = fist[S];
	while(!q.empty())
	{
		int u = q.front(); q.pop();
		for(int i = fist[u]; i != -1; i = line[i].nxt)
		{
			int v = line[i].to;
			if(d[v] == -1 && line[i].flow)
			{
				d[v] = d[u] + 1;
				cur[v] = fist[v];
				if(v == T) return 1;
				q.push(v);
			}
		}
	}
	return 0;
}

int find(int u, int limit)
{
	if(u == T) return limit;
	int flow = 0;
	for(int i = cur[u]; i != -1 && flow < limit; i = line[i].nxt)
	{
		cur[u] = i;
		int v = line[i].to;
		if(d[v] == d[u] + 1 && line[i].flow)
		{
			int t = find(v, min(line[i].flow, limit - flow));
			if(!t) d[v] = -1;
			line[i].flow -= t;
			line[i ^ 1].flow += t;
			flow += t;
		}
	}	
	return flow;
}

int dinic()
{
	int res = 0, flow;
	while(bfs()) while(flow = find(S, INF)) res += flow;
	return res;	
}

bool check(int mid)
{
	for(int i = 0; i < idx; ++ i)
		if(line[i].w > mid) line[i].flow = 0;
		else line[i].flow = 1;
	
	return dinic() >= k;	
}

int main()
{
	scanf("%d%d%d", &n, &m, &k);
	S = 1, T = n;
	memset(fist, -1, sizeof fist);
	for(int i = 1; i <= m; ++ i)
	{
		int a, b, c;
		scanf("%d%d%d", &a, &b, &c);
		add(a, b, c);
	} 
	
	int l = 1, r = 1e6, res;
	while(l <= r)
	{
		int mid = l + r >> 1;
		if(check(mid))
		{
			res = mid;
			r = mid - 1;
		}
		else l = mid + 1;
	}
	printf("%d
", res);
	return 0;
}

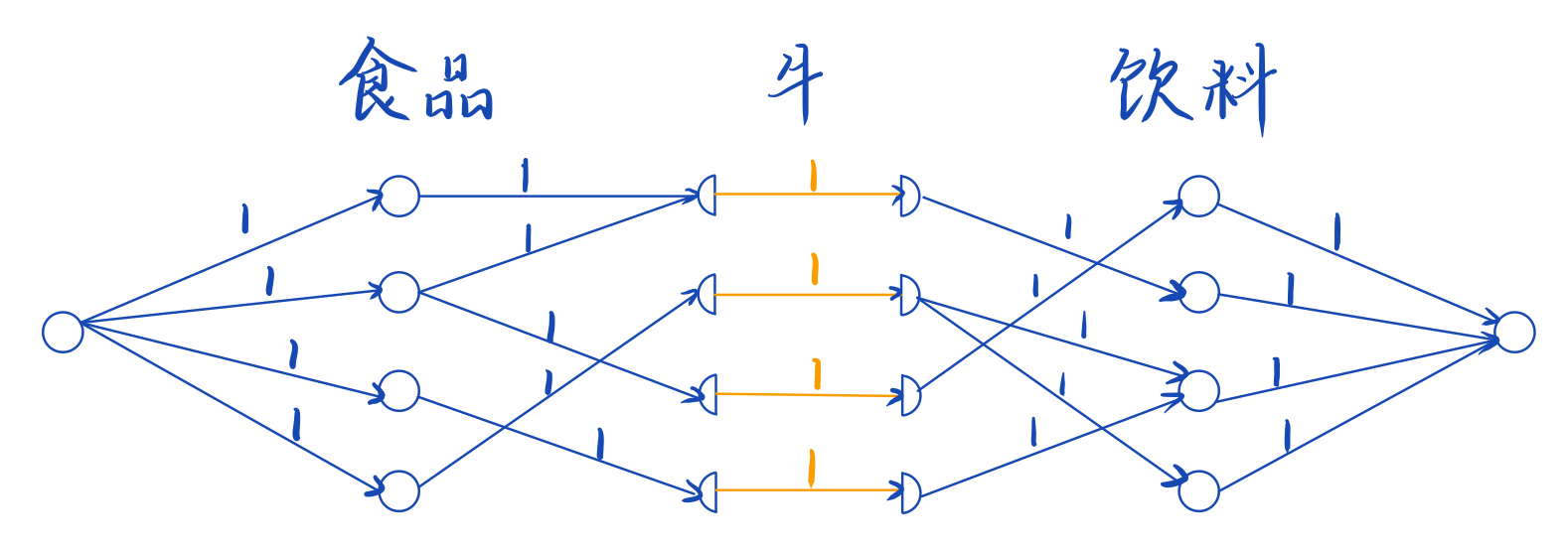
餐饮

三分图匹配（拆点）
建图方式与二分图匹配类似
防止一头牛被多次选择，把牛拆成两个点，入点和出点，限制加在入点和出点的边上，即设置容量为 (1)
(把对点的限制转化到入点到出点的边的容量上）

#include <bits/stdc++.h>
using namespace std;

const int N = 400 + 10;
const int M = (20000 + 300 + 10) * 2;
const int INF = 1e9;

int n, F, D, S, T;
struct Edge
{
	int to, nxt, flow;
}line[M];
int fist[N], idx;
int cur[N], d[N];

void add(int x, int y, int z)
{
	line[idx] = {y, fist[x], z};
	fist[x] = idx ++;
	line[idx] = {x, fist[y], 0};
	fist[y] = idx ++;
} 

bool bfs()
{
	queue<int> q;
	memset(d, -1, sizeof d);
	q.push(S), d[S] = 0, cur[S] = fist[S];
	while(!q.empty())
	{
		int u = q.front(); q.pop();
		for(int i = fist[u]; i != -1; i = line[i].nxt)
		{
			int v = line[i].to;
			if(d[v] == -1 && line[i].flow)
			{
				d[v] = d[u] + 1;
				cur[v] = fist[v];
				if(v == T) return 1;
				q.push(v);
			}
		}
	} 
	return 0;
}

int find(int u, int limit)
{
	if(u == T) return limit;
	int flow = 0;
	for(int i = cur[u]; i != -1 && flow < limit; i = line[i].nxt)
	{
		cur[u] = i;
		int v = line[i].to;
		if(d[v] == d[u] + 1 && line[i].flow)
		{
			int t = find(v, min(line[i].flow, limit - flow));
			if(!t) d[v] = -1;
			line[i].flow -= t;
			line[i ^ 1].flow += t;
			flow += t;
		}
	}
	return flow;
}

int dinic()
{
	int res = 0, flow;
	while(bfs()) while(flow = find(S, INF)) res += flow;
	return res;	
}

int main()
{
	scanf("%d%d%d", &n, &F, &D);
	S = 0, T = n * 2 + F + D + 1;
	memset(fist, -1, sizeof fist);
	for(int i = 1; i <= F; ++ i) add(S, n * 2 + i, 1);
	for(int i = 1; i <= D; ++ i) add(n * 2 + F + i, T, 1);
	for(int i = 1; i <= n; ++ i)
	{
		add(i, n + i, 1);
		int a, b, t;
		scanf("%d%d", &a, &b);
		while(a -- )
		{
			scanf("%d", &t);
			add(n * 2 + t, i, 1);
		}
		while(b -- )
		{
			scanf("%d", &t);
			add(n + i, n * 2 + F + t, 1);
		}
	}
	printf("%d
", dinic());
	return 0;
} 

企鹅游行

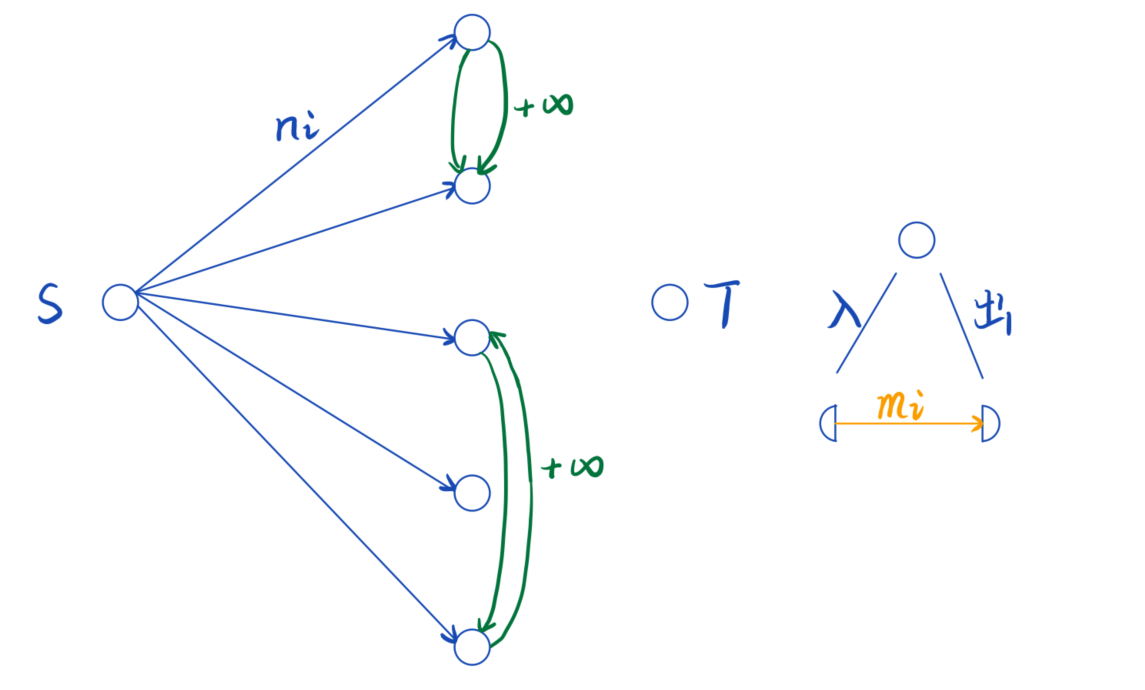
把冰块当做点， 企鹅当成流量， 起跳限制在点上， 考虑拆点

• 从源点向每个冰块连一条容量为初始企鹅数量的边
• 可以相互到达的冰块之间连两条容量为 (+infty) 的边
• 考虑每个冰块的起跳限制，把每个冰块拆成入点和出点，从入点向出点连一条容量为起跳限制的边
• 枚举每个点作为汇点， 判断最大流是否满流
  

#include <bits/stdc++.h>
using namespace std;

#define x first
#define y second
typedef pair<int, int> PII;

const int N = 100 * 2 + 10;
const int M = (100 * 2 + 100 * 100 + 10) * 2;
const int INF = 1e9;
const double eps = 1e-8;

int n, S, T;
double D;
struct Edge
{
	int to, nxt, flow;
}line[M];
int fist[N], idx;
int cur[N], d[N];
PII p[N];

bool check(PII a, PII b)
{
	double dx = a.x - b.x, dy = a.y - b.y;
	return dx * dx + dy * dy < D * D + eps;
}

void add(int x, int y, int z)
{
	line[idx] = {y, fist[x], z};
	fist[x] = idx ++;
	line[idx] = {x, fist[y], 0};
	fist[y] = idx ++;
}

bool bfs()
{
	queue<int> q;
	memset(d, -1, sizeof d);
	q.push(S), d[S] = 0, cur[S] = fist[S];
	while(!q.empty())
	{
		int u = q.front(); q.pop();
		for(int i = fist[u]; i != -1; i = line[i].nxt)
		{
			int v = line[i].to;
			if(d[v] == -1 && line[i].flow)
			{
				d[v] = d[u] + 1;
				cur[v] = fist[v];
				if(v == T) return 1;
				q.push(v);
			} 
		} 
	}
	return 0;
}

int find(int u, int limit)
{
	if(u == T) return limit;
	int flow = 0;
	for(int i = cur[u]; i != -1 && flow < limit; i = line[i].nxt)
	{
		cur[u] = i;
		int v = line[i].to;
		if(d[v] == d[u] + 1 && line[i].flow)
		{
			int t = find(v, min(line[i].flow, limit - flow));
			if(!t) d[v] = -1;
			line[i].flow -= t;
			line[i ^ 1].flow += t;
			flow += t;
		}
	}
	return flow;
}

int dinic()
{
	int res = 0, flow;
	while(bfs()) while(flow = find(S, INF)) res += flow;
	return res;
}

int main()
{
	int __;
	scanf("%d", &__);
	while(__ -- )
	{
		memset(fist, -1, sizeof fist);
		idx = 0;
		scanf("%d%lf", &n, &D);
		S = 0;
		int tot = 0;
		for(int i = 1; i <= n; ++ i)
		{
			int x, y, a, b;
			scanf("%d%d%d%d", &x, &y, &a, &b);
			p[i] = {x, y};
			tot += a;
			add(S, i, a);
			add(i, i + n, b);
		}
		for(int i = 1; i <= n; ++ i)
			for(int j = i + 1; j <= n; ++ j)
				if(check(p[i], p[j]))
				{
					add(i + n, j, INF);
					add(j + n, i, INF);
				}
		int cnt = 0;
		for(int i = 1; i <= n; ++ i)
		{
			T = i;
			for(int j = 0; j < idx; j += 2)
			{
				line[j].flow += line[j ^ 1].flow;
				line[j ^ 1].flow = 0;
			} 
			if(dinic() == tot) 
			{
				printf("%d ", i - 1);
				++ cnt; 
			} 
		}
		if(!cnt) puts("-1");
		else puts("");
	}
	return 0;
}

猪

把猪舍看成点， 猪看做流量

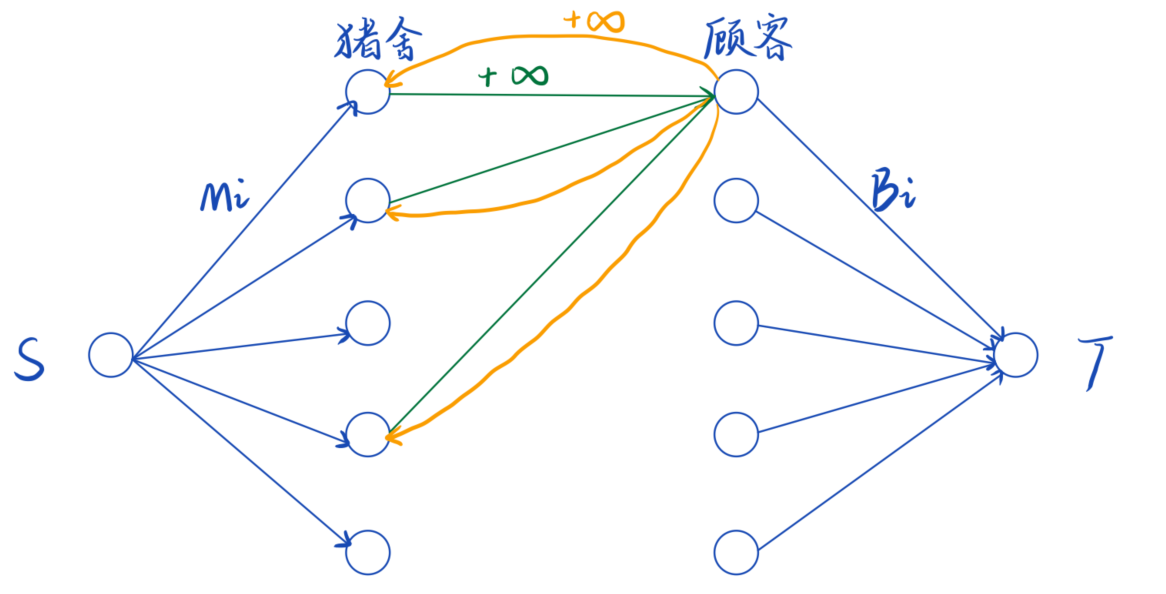
考虑一种建图方式：

• 从源点向每个猪舍连一条容量为初始猪的数量的边
• 从每个顾客向汇点连一条容量为购买数量的边
• 从顾客可以打开的猪舍向该顾客连一条容量为 (+infty) 的边， 再从顾客向这些猪舍连一条容量为 (+infty) 的边
  

上述的建图方式没有考虑时序性，造成后来的顾客可以先调整猪舍
考虑一种考虑时序的新的建图方式，不考虑猪舍， 认为顾客可以把猪暂存， 使猪在顾客间流动

• 若某猪舍第一次被打开， 则该顾客可以取的就是初始猪的数量， 从源点向顾客连一条容量为初始猪的边
• 若某猪舍不是第一次被打开， 就从上一个打开这个猪舍的顾客向当前顾客连一条容量为 (+infty) 的边
• 从每个顾客向汇点连一条容量为购买数量的边
  

#include <bits/stdc++.h>
using namespace std;

const int N = 100 + 10;
const int M = (100 * 1000 + N + 10) * 2;
const int INF = 1e9;

int n, m, S, T;
struct Edge
{
	int to, nxt, flow;
}line[M];
int fist[N], idx;
int cur[N], d[N];
int w[1010], last[1010];

void add(int x, int y, int z)
{
	line[idx] = {y, fist[x], z};
	fist[x] = idx ++;
	line[idx] = {x, fist[y], 0};
	fist[y] = idx ++; 
} 

bool bfs()
{
	queue<int> q;
	memset(d, -1, sizeof d);
	q.push(S), d[S] = 0, cur[S] = fist[S];
	while(!q.empty())
	{
		int u = q.front(); q.pop();
		for(int i = fist[u]; i != -1; i = line[i].nxt)
		{
			int v = line[i].to;
			if(d[v] == -1 && line[i].flow)
			{
				d[v] = d[u] + 1;
				cur[v] = fist[v];
				if(v == T) return 1;
				q.push(v); 
			}
		}
	}
	return 0;
}

int find(int u, int limit)
{
	if(u == T) return limit;
	int flow = 0;
	for(int i = cur[u]; i != -1 && flow < limit; i = line[i].nxt)
	{
		cur[u] = i;
		int v = line[i].to;
		if(d[v] == d[u] + 1 && line[i].flow)
		{
			int t = find(v, min(line[i].flow, limit - flow));
			if(!t) d[v] = -1;
			line[i].flow -= t;
			line[i ^ 1].flow += t;
			flow += t;
		}
	}
	return flow;
}

int dinic()
{
	int res = 0, flow;
	while(bfs()) while(flow = find(S, INF)) res += flow;
	return res;
}

int main()
{
	scanf("%d%d", &m, &n);
	S = 0, T = n + 1;
	memset(fist, -1, sizeof fist);
	for(int i = 1; i <= m; ++ i) scanf("%d", &w[i]);
	for(int i = 1; i <= n; ++ i)
	{
		int a, k, b;
		scanf("%d", &a);
		while(a -- )
		{
			scanf("%d", &k);
			if(!last[k]) add(S, i, w[k]);
			else add(last[k], i, INF);
			last[k] = i;
		}
		scanf("%d", &b);
		add(i, T, b);
	}
	printf("%d
", dinic());
	return 0;
}