堆排序
堆排序(Heap Sort)算法是基于选择排序思想的算法,其利用堆结构和二叉树的一些性质来完成数据的排序。
什么是堆结构
堆排序的关键是首先构造堆结构。那么什么是堆结构呢?堆结构是一种树结构,准确地说是一个完全二叉树。在这个树中每个结点对应于原始数据的一个记录,并且每个结点应满足以下条件:
・如果按照从小到大的顺序排序,要求非叶结点的数据要大于或等于其左、右子结点的数据。
・如果按照从大到小的顺序排序,要求非叶结点的数据要小于或等于其左、右子结点的数据。
堆排序过程
一个完整的堆排序需要经过反复的两个步骤:构造堆结构和堆排序输出。下面首先分析如果构造堆结构。
构造堆结构
构造堆结构就是把原始的无序数据按前面堆结构的定义进行调整。首先,需要将原始的无序数据放置到一个完全二叉树的各个结点中,这可以按照前面介绍的方法来实现。
然后,由完全二叉树的下层向上层逐层对父子结点的数据进行比较,使父结点的数据大于子结点的数据。这里需要使用“筛”运算进行结点数据的调整,直到所有结点最后满足堆结构的条件为止。筛运算主要针对非叶结点进行调整。
例如,对于一个非叶结点Ai,假定Ai的左子树和右子树均已进行筛运算,也就是说其左子树和右子树均已构成堆结构。对Ai进行筛运算,操作步骤如下:
(1)比较Ai的左子树和右子树的最大值,将最大值放在Aj中。
(2)将Ai的数据与Aj的数据进行比较,如果Ai大于等于Aj,表示以Ai为根的子树已构成堆结构。便可以终止筛运算。
(3)如果Ai小于Aj,则将Ai与Aj互换位置。
(4)经过第(3)步后,可能会破坏以Ai为根的堆,因为此时Ai的值为原来的Aj。下面以Aj为根重复前面的步骤,直到满足堆结构的定义,即父结点数据大于子结点。这样,以Aj为根的子树就被调整为一个堆。
在执行筛运算时,值较小的数据将逐层下移,这就是其称为“筛”运算的原因。
堆排序
(1)根据堆结构的特点,堆结构的根结点也就是最大值。这里按照从小到大排序,因此将其放到数组的最后。
(2)对除最后一个结点外的其他结点重新执行前面介绍的构造堆过程。
(3)重复上述过程,取此时堆结构的根结点(最大值)进行交换,放在数组的后面。
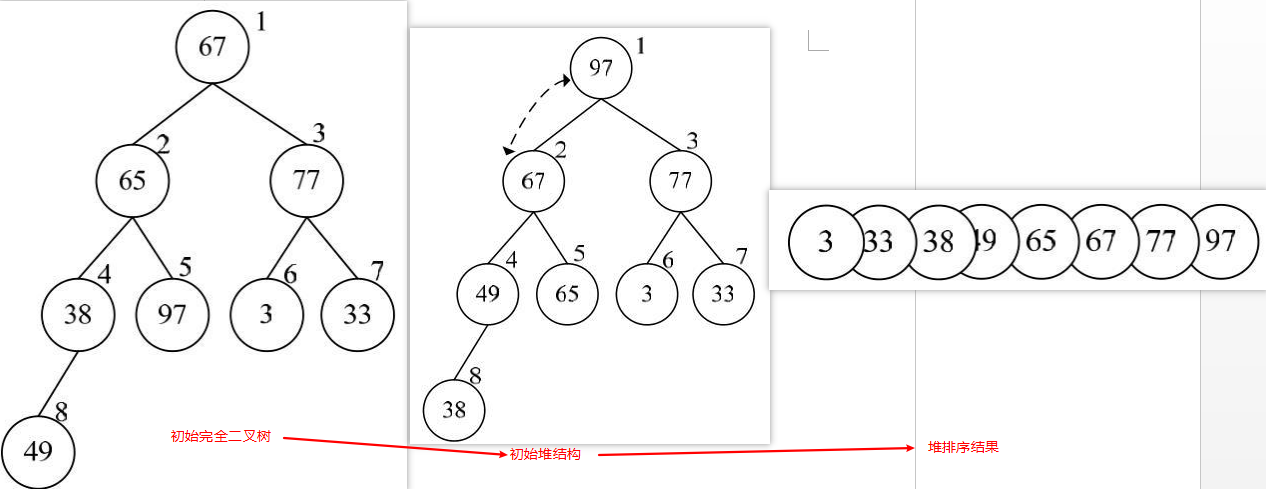
动图演示

示例:
public class ClassP4_6 { static void constructHeap(int[] arr, int length_n) { int j, temp; // 构建堆结构 for (int i = length_n / 2 - 1; i >= 0; i--) {//i为 非叶子节点 while (2 * i + 1 < length_n) {//i节点有左子树 j = 2 * i + 1;//j为 左子树 if (j + 1 < length_n) { if (arr[j] < arr[j + 1]) {//左子树 小于 右子树,则需要比较右子树 j++;//指向右子树 } } if (arr[i] < arr[j]) { //交换 非叶子节点 和 左右树节点中的最大值 temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; System.out.println("i:" + i + ",j:" + j + "交换:" + ArrayUtils.toString(arr)); i = j;//堆被破坏,重新调整 } else { break; } } } } static void heapSort(int[] arr) { int length = arr.length; int temp; constructHeap(arr, length); for (int i = length - 1; i > 0; i--) { System.out.println(i + ArrayUtils.toString(arr)); // 交换 根节点(最大值) 和最后1个节点 temp = arr[0]; arr[0] = arr[i]; arr[i] = temp;//每次都把最大值放到 剩下节点的最后1个节点 constructHeap(arr, i);//对剩下的节点 构建堆结构 } System.out.println(ArrayUtils.toString(arr)); } public static void main(String[] args) { // constructHeap(new int[]{0, 1, 2, 3, 4, 5, 6, 7}, 8); heapSort(new int[]{0, 1, 2, 3, 4, 5, 6, 7}); } }
结果:
i:3,j:7交换:{0,1,2,7,4,5,6,3}
i:2,j:6交换:{0,1,6,7,4,5,2,3}
i:1,j:3交换:{0,7,6,1,4,5,2,3}
i:3,j:7交换:{0,7,6,3,4,5,2,1}
i:0,j:1交换:{7,0,6,3,4,5,2,1}
i:1,j:4交换:{7,4,6,3,0,5,2,1}
7{7,4,6,3,0,5,2,1}
i:0,j:2交换:{6,4,1,3,0,5,2,7}
i:2,j:5交换:{6,4,5,3,0,1,2,7}
6{6,4,5,3,0,1,2,7}
i:0,j:2交换:{5,4,2,3,0,1,6,7}
5{5,4,2,3,0,1,6,7}
i:0,j:1交换:{4,1,2,3,0,5,6,7}
i:1,j:3交换:{4,3,2,1,0,5,6,7}
4{4,3,2,1,0,5,6,7}
i:0,j:1交换:{3,0,2,1,4,5,6,7}
i:1,j:3交换:{3,1,2,0,4,5,6,7}
3{3,1,2,0,4,5,6,7}
i:0,j:2交换:{2,1,0,3,4,5,6,7}
2{2,1,0,3,4,5,6,7}
i:0,j:1交换:{1,0,2,3,4,5,6,7}
1{1,0,2,3,4,5,6,7}
{0,1,2,3,4,5,6,7}
参考:Java常用算法手册4.7