大约是一颗李超线段树

%%%李超

由于观看Joe大神颓废学习发现了这种高级数据结构

才引来了这场灾难（我先改完T2才改完T1

说明书：

用途：维护最优一次函数

复杂度：$Theta (n log_{2}n^{2})$

食使用指南:

我们先把线段树节点中存储的信息改为存储一条线

存储的线段不一定在区间的每个点上都最有,但是应该是在该区间最优的

有没有感觉很像二维MLE线段树

当然也可能有这么两条线分别在同一区间不同位置最优

此时维护优的区间更长的

(以下假设维护最大值

区间修改:

　　我们考虑两根线段

　　首先我们要将线段在线段树上定位,此时会有$ log_{2}n$个区间需要修改

　　接下来我们只考虑一个区间了哈

　　经对两根线段的相对位置大力分类讨论得:

　　一共有四种情况

　　1.

　　　　

 　   线段$a$(蓝色)的斜率比当前最优线段$b$(或许是橙色)小

　　且两线段交点在中点右侧

　　那么显然对于当前区间以及左侧区间线段$a$更优,

　　递归到这里就可以停了(当前区间已经被修改后再去修改左侧区间毫无意义

　　但是对于右侧区间

　　线段$b$仍可能更优

　　此时应以线段$b$为参数递归修改右侧区间

　　2.

　　　

 　   线段$a$(同上)的斜率比当前最优线段$b$(同上)小

　　且两线段交点在中点左侧

　　线段$a$仅在左侧区间可能更优

　　此时应以线段$a$为参数递归修改左侧区间

　　3.

　　

       线段$a$(同上)的斜率比当前最优线段$b$(同上)大

　　且两线段交点在中点右侧

　　线段$a$仅在右侧区间可能更优

　　此时应以线段$a$为参数递归修改右侧区间

　　4.

　　

 　　

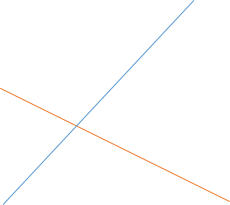
       线段$a$(同上)的斜率比当前最优线段$b$(同上)大

　　且两线段交点在中点左侧

　　对于当前区间以及左侧区间线段$b$更优,

　　此时应以线段$b$为参数递归修改左侧区间

单点查询:

　　正常查询即可

　　注意应在每个节点取一次最值

　　因为最优解及可能来自叶节点

　　也有可能来自祖先节点

另附本次考试T1代码:

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define cin(k) scanf("%lld",&k)
#define l(k) ((k)<<1)
#define r(k) (l(k)|1)
const int maxn=64646,base=32323;
struct line{int k,b;};
struct Tree{
	struct tree{
		int bo;
		line li;
	}t[base<<3];
	bool cmp(int p,line x,line y)
	{
		p-=base;
		return x.k*p+x.b>=y.k*p+y.b;
	}
	void add(int k,int l,int r,line li)
	{
		if(l==r)
		{
			if(cmp(l,li,t[k].li))	t[k].li=li;
			return;
		}
		int mid=(l+r)>>1;
		if(t[k].li.k<=li.k)
		{
			if(cmp(mid,li,t[k].li))
			{
				add(l(k),l,mid,t[k].li);
				t[k].li=li;
			}
			else
				add(r(k),mid+1,r,li);
		}
		else
		{
			if(cmp(mid,li,t[k].li))
			{
				add(r(k),mid+1,r,t[k].li);
				t[k].li=li;
			}
			else
				add(l(k),l,mid,li);
		}
	}
	int query(int k,int l,int r,int p,int res)
	{
		int ans=t[k].li.k*(p-base)+t[k].li.b;
		if(l==r)	return ans;
		int mid=(l+r)>>1;
//		if(res)
		{
			if(p<=mid)	return max(ans,query(l(k),l,mid,p,res));
			else		return max(ans,query(r(k),mid+1,r,p,res));
		}
/*		else
		{
			if(p<=mid)	return min(ans,query(l(k),l,mid,p,res));
			else		return min(ans,query(r(k),mid+1,r,p,res));
		}
*/	}
}S,T;
int n,qu;
int ans[maxn+1];
signed main()
{
	freopen("A.in","r",stdin);
	freopen("A.out","w",stdout);
	cin(n);cin(qu);
	for(int q=1;q<=n;q++)
	{
		int a,b;cin(a),cin(b);
		S.add(1,base+1,maxn,(line){a,b});
		T.add(1,1,base-1,(line){-a,-b});
	}
	for(int q=-32322;q<=32322;q++)
	{
		if(q>0)			ans[q+base]=S.query(1,base+1,maxn,q+base,1)*q;
		else if(q<0)	ans[q+base]=-T.query(1,1,base-1,q+base,0)*q;
		else			ans[q+base]=0;
	}
	for(int q=1;q<=qu;q++)
	{
		int x;cin(x);
		printf("%lld
",ans[x+base]);
	}
}

区间查询:

　　好像和二维线段树区间查询很像,自己yy吧(其实是我懒

作者已死(死因:调上方代码所致