最小二乘法拟合三维直线
在《高等数学》的书中给出了最小二乘法拟合直线的具体实例,但是那个例子是拟合二维直线的f(t)=at+b,那么三维直线怎么使用最小二乘法来拟合呢?我们先来看看《高等数学》书中的例子,由于任何实数的平方都是正数或零,因此我们可以考虑选取常数a, b,使
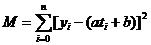
M最小来保证每个偏差的绝对值都很小,这种根据偏差的平方和为最小的条件来选择常数a, b的方法叫做最小二乘法(Least Square)。因为M是平方和,所以M的最小值在导数等于零的时候取得,即:

根据这个条件计算得到的最小值就是最小二乘解。因为拟合函数是二维直线方程f(t)=at+b是线性的,所以二维直线的拟合是线性最小二乘问题。对于三维直线,如果选择其代数方程,是两个平面的交线来表达的:

可以看出待确定的参数有8个,不是一个好办法。可以采用直线的参数表达,根据直线的对称式方程导出直线的参数方程:
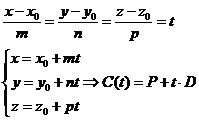
我们要做的是根据N个采样点Pi确定参数方程的P和D,使所有采样点到直线的距离的平方和最小。对于三维点到三维直线的距离我们可以使用矢量方法来计算,可以参考《点向直线投影》,
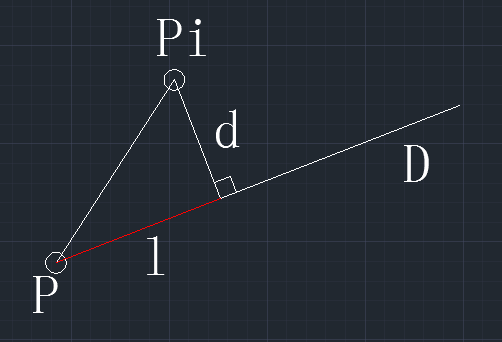
向量V为P到采样点Pi的向量,向量D为直线的方向向量,是单位向量。V和D点乘得到V向D的投影长度,即图中红色标示部分的长度l。则采样点到直线的距离的平方是向量V的模的平方减去投影长度l的平方。从而得到采样点到直线的距离平方和方程:
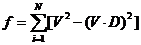
参考“最小二乘法三维(k维)直线拟合http://www.whudj.cn/?p=72”可知,最小二乘法拟合的直线通过所有采样点的中心点。即可以确定直线参数方程中的P。这样最小二乘方程就是只有方向矢量的一个多元函数。使用类math_MultipleVarFunctionWithGradient来建立上述最小二乘方程:
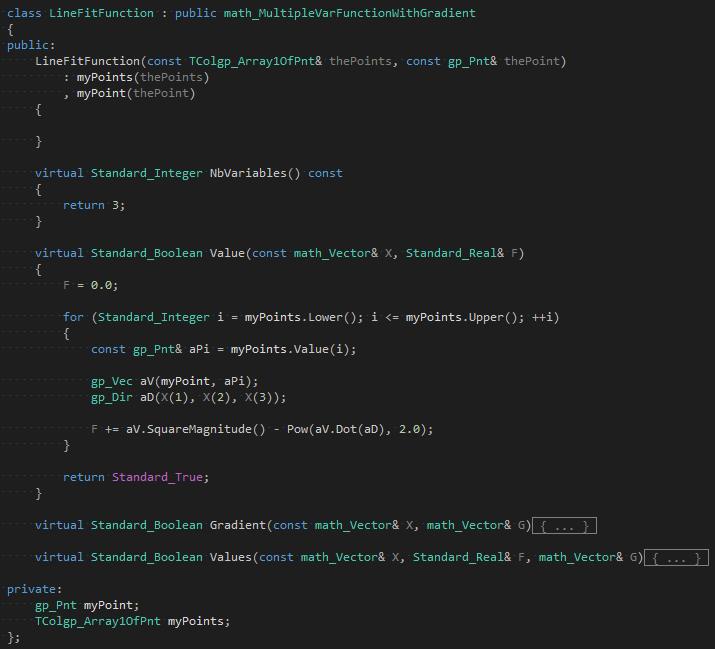
其中成员变量myPoint是直线的中心点,myPoints是所有的采样点。最小二乘方程为确定直线参数方程中的方向矢量(dx, dy, dz)的三个变量方程。使用math_BFGS之类的非线性极值计算类来对这个最小二乘方程进行求解。下面给出几个测试用例:
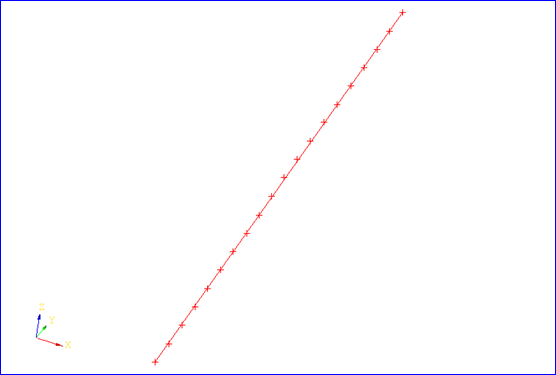
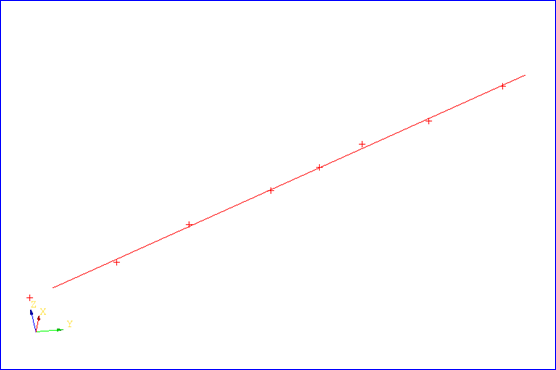
综上所述,拟合三维直线的最小二乘方程中点到直线的距离为点到直线的垂直距离,而书中二维直线拟合只是两个y值之间的差值:
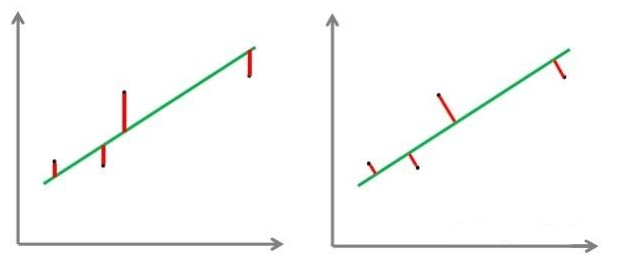
图 点到直线的距离 (来自:https://zhuanlan.zhihu.com/p/36429715)
上述拟合过程也可看出三维直线的拟合是一个非线性的优化问题,处理这类问题的一般步骤就是先建立目标方程,再使用相关优化求解类来对方程进行求解。