Mesh BRep Shapes
Abstract. 当对OpenCASCADE的BRep表示法的数据结构有了一定的理解后,建议可以自己实现一个显示数据生成的功能,即网格剖分功能。
Key Words. BRep, Mesh, Triangulation
1. Introduction
在OpenCASCADE中网格剖分功能是很重要的一个模块,他可用于生成模型的可视化数据,还可用于HLR消隐,对于离散求交算法也是基于网格数据。OpenCASCADE开源版本中的模块TKMesh可以用来生成网格的显示数据,主要的类为BRepMesh_IncrementalMesh。
在使用BRepMesh_IncrementalMesh的过程中发现其剖分精度高,且精度不便于控制。如对一个球进行网格剖分,想得到一个粗糙的效果,即一个多边形,使用BRepMesh_IncrementalMesh是不容易得到的。
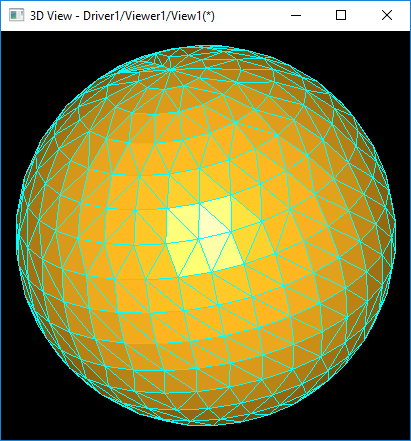
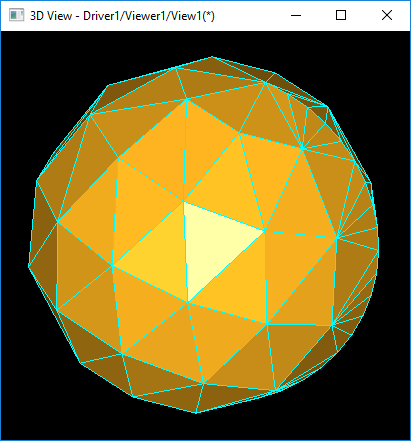
如上图所示为同一个球的不同的剖分精度得到的模型。为了能精确控制网格剖分精度,以便后期使用LOD等优化算法,自己实现一个网格剖分功能。
网格剖分的主要思路就是遍历每个TopoDS_Face的TopoDS_Wire,根据Wire找到边界或面上的孔洞。将Wire对应到二维参数空间,并对二维参数空间中的边界先进行一次三角网格剖分。对于平面来说,只需要这一步就可以满足可视化的要求。对于其他曲面来说,就需要在二维参数空间中额外插入一些点,以使最终生成的网格满足剖分精度要求。最后将二维参数空间的三角剖分映射到三维空间。
2. Mesh Boundary Region
因为使用BRepBuilderAPI_MakeFace可以通过Add(TopoDS_Wire)来添加面上的开孔,所以一个TopoDS_Face会有大于1个的TopoDS_Wire。找出外边界和内孔Wire后可进行一次三角剖分,如下图所示:
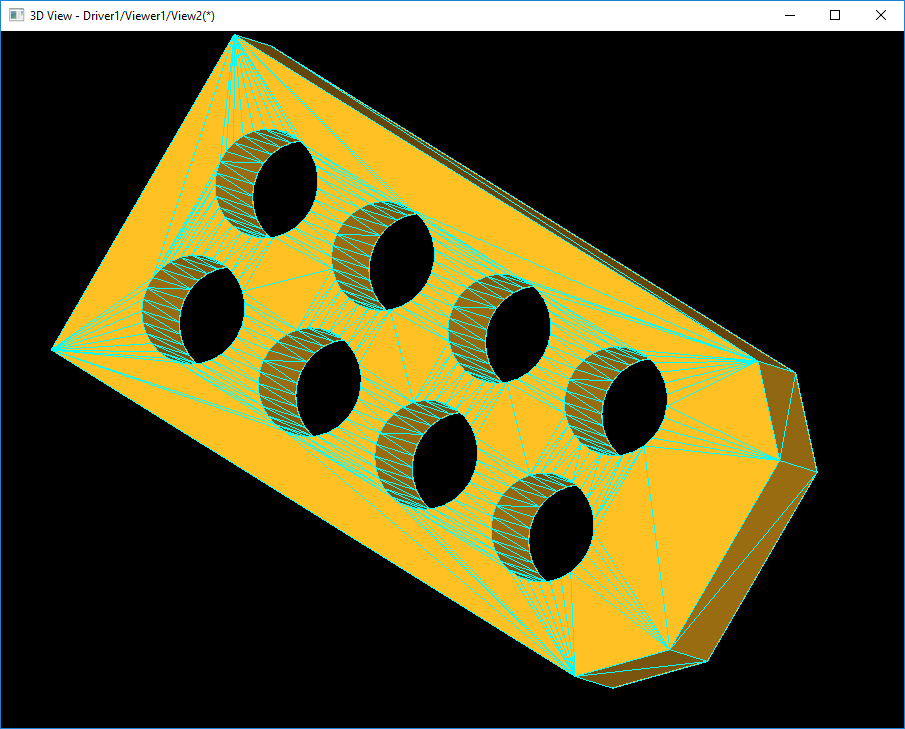
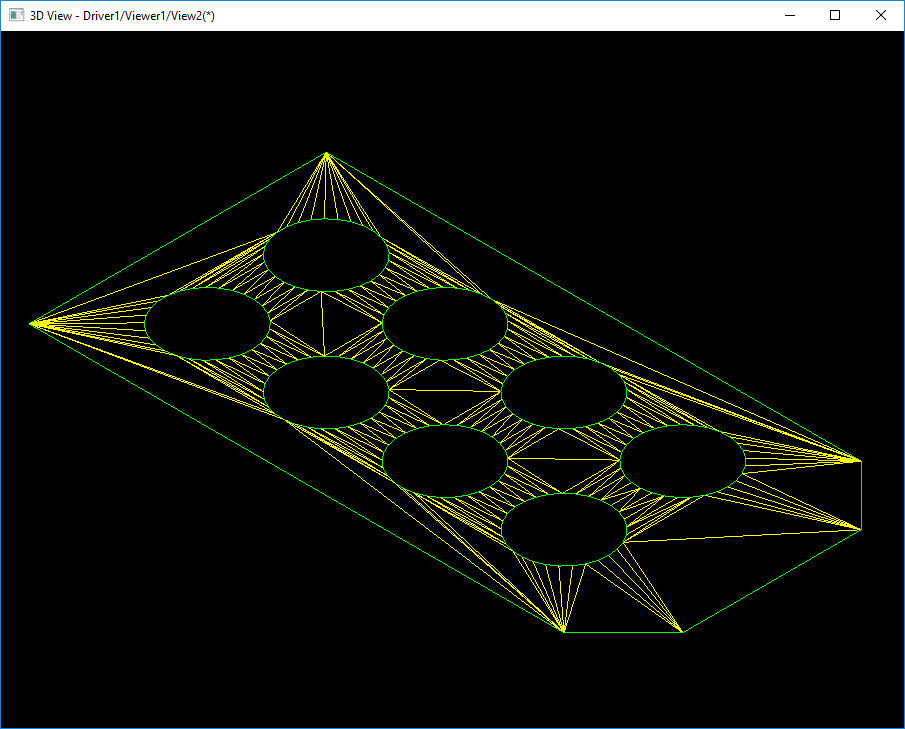
如上图所示,对于平面而言,直接对边界及内孔进行一次三角剖分即可以得到满意的网格数据。对于曲面而言,这显然是不满足精度要求的。
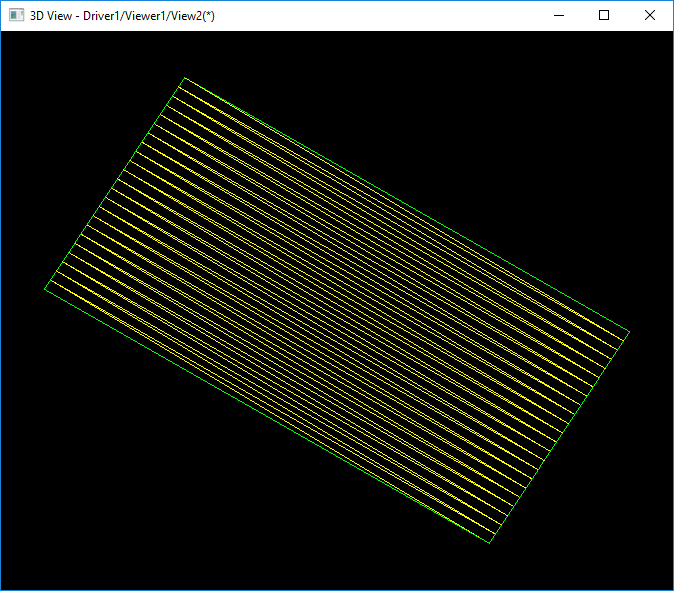
如上图所示为球面的第一次对边界进行三角剖分得到的效果。因为在一个参数上的边是退化Degenerated边,所以退化边的参数空间上没有均分。将参数空间的三角剖分映射到三维空间后,得到的是一条线,其实是两个非退化边。
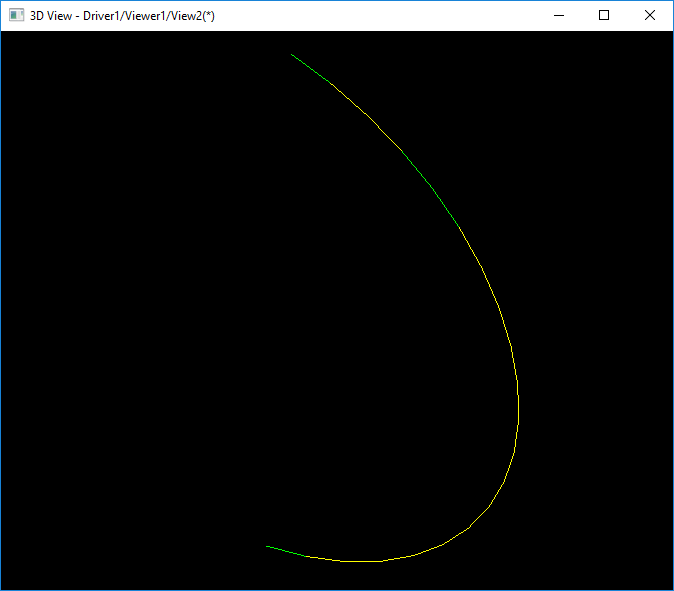
3. Deflection Control
对于曲面来说,如果直对边界进行一次三角剖分,是达不到精度要求。为了使曲面网格剖分效果更好,就需要对按边界剖分后的网格进行插入点继续剖分。对于上面球面的参数空间区域,根据精度要求插入点剖分后的结果如下图所示:
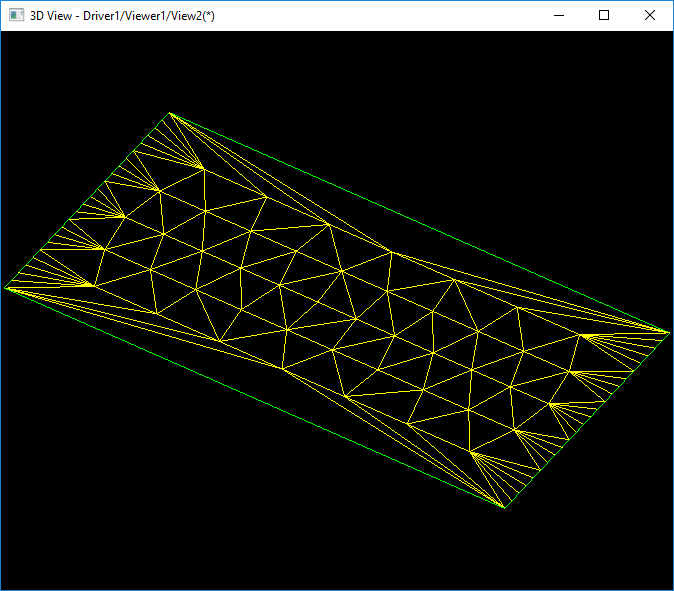
得到的三维效果如下图所示:
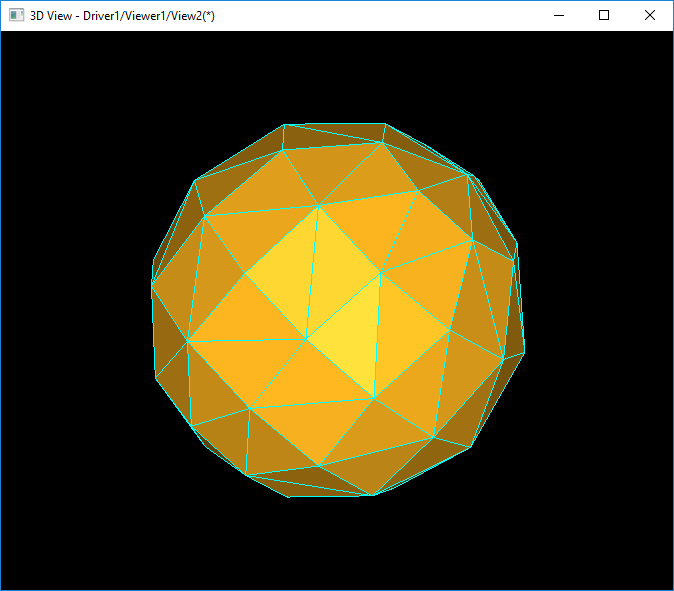
4. Demo
下面给出几个自己实现网格剖分的结果与OpenCASCADE的TKMesh作个对比:
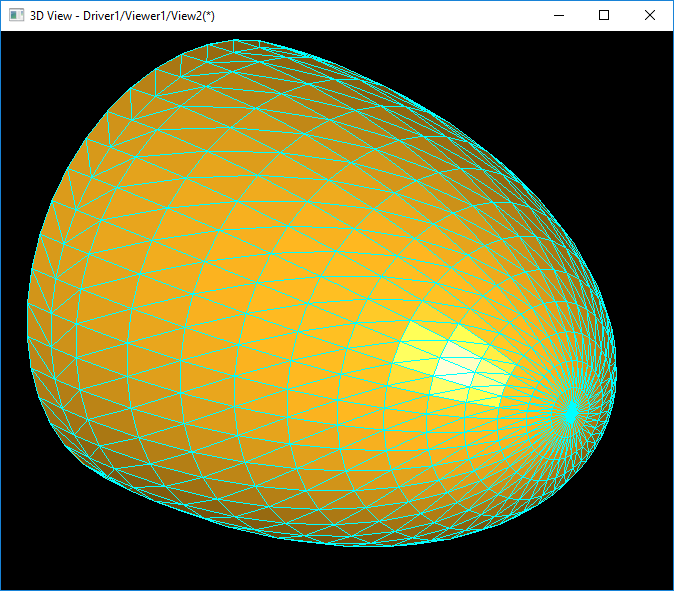
上图为自己实现网格剖分算法对椭球面的网格剖分结果
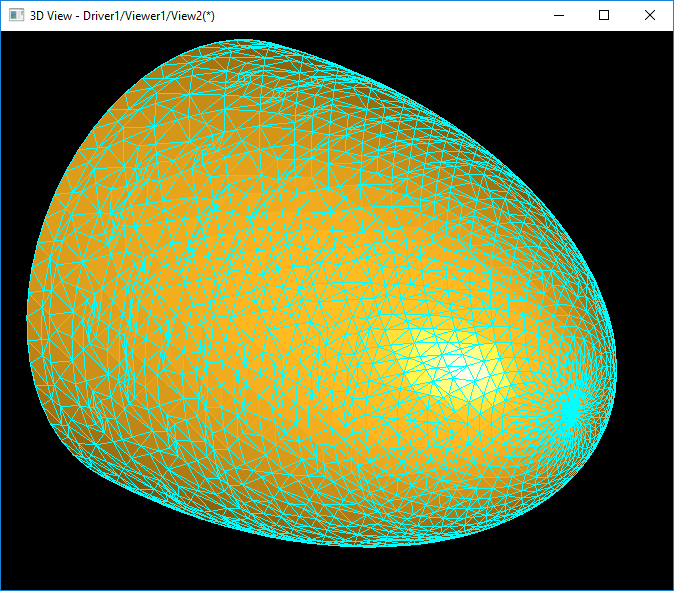
上图为TKMesh网格剖分算法对椭球面的网格剖分结果
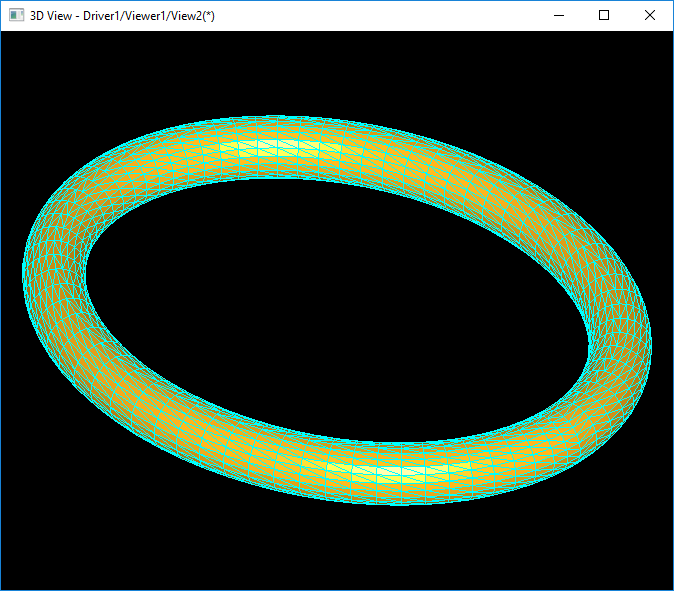
上图为自己实现网格剖分算法对椭圆环面的网格剖分结果
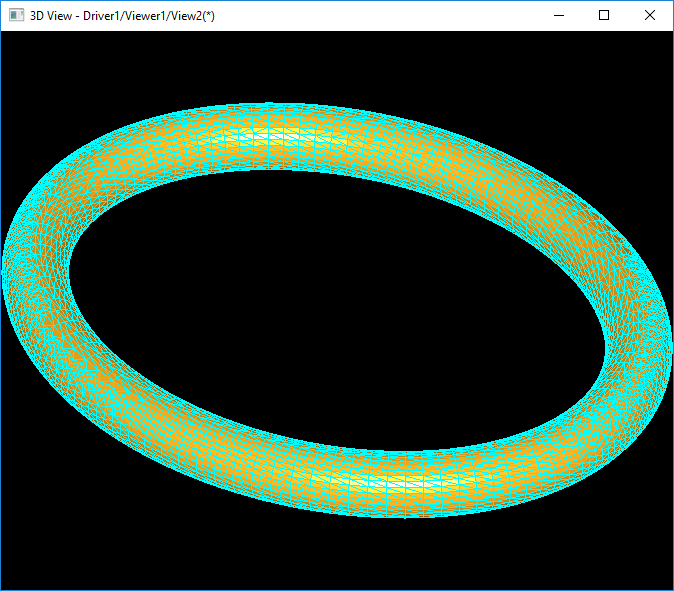
上图为TKMesh网格剖分算法对椭圆环面的网格剖分结果
通过上面的对比可以发现,在大致相同的显示效果情况下,OpenCASCADE产生了更多的顶点和三角形数据。自己实现的网格剖分产生的网格质量相对可控且性能高。
5. Conclusion
OpenCASCADE中开源的网格剖分库TKMesh可以实现模型的可视化数据生成功能,但是对于网格剖分的精度可控性差。为了对模型的网格精度进行更好地控制,自己实现一套网格剖分功能,且性能要优于TKMesh。在程序的编写过程中,可以加深BREP数据结构中一些概念的理解。有兴趣的读者在熟悉BREP数据结构后,也可以尝试下网格剖分功能的实现。