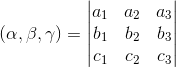设两向量分别为 α 和 β,
- 数量积
α • β = |α| |β| cosθ (θ 为向量 α 和 β 的夹角)
通过公式我们可以发现,两个向量的数量积就是一个数量。
数量积又称为点积或者内积。
ex: 在直角坐标系 {O; i, j, k} 中,设 α = (a1, a2, a3), β = (b1, b2, b3),
α • β = (a1i + a2j + a3k) • (b1i + b2j + b3k) = a1b1 + a2b2 + a3b3
即两向量的数量积之和等于它们对应坐标的乘积之和。
- 向量积
向量积是一个向量,通常表示为 α χ β ,
1. 它的模(即长度)为 |α χ β| = |α| |β| sinθ (θ 为向量 α 和 β 的夹角)
2. 方向垂直于向量 α 和 β,且 (α, β, α χ β) 构成右手系。
向量积又称为叉积和外积。
ex: 在直角坐标系 {O; i, j, k} 中,设 α = (a1, a2, a3), β = (b1, b2, b3),
α χ β = (a1i + a2j + a3k) χ (b1i + b2j + b3k)
= (a2b3 - a3b2)i - (a1b3 - a3b1)j + (a1b2 - a2b1)k
行列式表示为
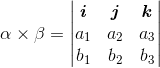
即
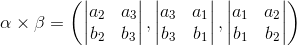
- 混合积
向量α 与 β 的向量积,再与向量 γ 作数量积,其结果为一个数量,称这个数量为
三向量的 α, β, γ 的混合积,记为 (α, β, γ), 即
(α, β, γ) = (α χ β) • γ
1. 三向量共面的充要条件为 (α, β, γ) = 0
2. (空间向量基本定理)任意给定空间中三个不共面向量 α, β, γ,则空间中任一
向量 ν 可以用 α, β, γ 唯一线性表示,即存在唯一一组实数 x, y, z 使
ν = xα + yβ + zγ
ex: 空间向量运算
在直角坐标系 {O; i, j, k} 中,设 α = (a1, a2, a3), β = (b1, b2, b3),
γ = (c1, c2, c3)
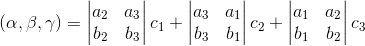
即