本文实例讲述了C#中yield return用法,并且对比了使用yield return与不使用yield return的情况,以便读者更好的进行理解。具体如下:
yield关键字用于遍历循环中,yield return用于返回IEnumerable<T>,yield break用于终止循环遍历。
有这样的一个int类型的集合:
|
1
2
3
4
|
static List<int> GetInitialData(){ return new List<int>(){1,2,3,4};} |
需要打印出所有值大于2的元素。
不使用yield return的实现
|
1
2
3
4
5
6
7
8
9
10
11
12
|
static IEnumerable<int> FilterWithoutYield(){ List<int> result = new List<int>(); foreach (int i in GetInitialData()) { if (i > 2) { result.Add(i); } } return result;} |
客户端调用:
|
1
2
3
4
5
6
7
8
|
static void Main(string[] args){ foreach (var item in FilterWithoutYield()) { Console.WriteLine(item); } Console.ReadKey(); } |
输出结果:3,4
使用yeild return实现
|
1
2
3
4
5
6
7
8
9
10
11
12
|
static IEnumerable<int> FilterWithYield(){ foreach (int i in GetInitialData()) { if (i > 2) { yield return i; } } yield break; Console.WriteLine("这里的代码不执行");} |
客户端调用:
|
1
2
3
4
5
6
7
8
|
static void Main(string[] args){ foreach (var item in FilterWithYield()) { Console.WriteLine(item); } Console.ReadKey(); } |
输出结果:3,4
总结:
通过单步调试发现:
虽然2种方法的输出结果是一样的,但运作过程迥然不同。第一种方法,是把结果集全部加载到内存中再遍历;第二种方法,客户端每调用一次,yield return就返回一个值给客户端,是"按需供给"。
第一种方法,客户端调用过程大致为:
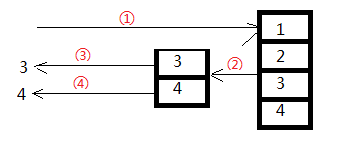
使用yield return,客户端调用过程大致为:

使用yield return为什么能保证每次循环遍历的时候从前一次停止的地方开始执行呢?
--因为,编译器会生成一个状态机来维护迭代器的状态。
简单地说,当希望获取一个IEnumerable<T>类型的集合,而不想把数据一次性加载到内存,就可以考虑使用yield return实现"按需供给"。