一、PTA题目
6-4 十进制转换二进制
1.设计思路
定义一个整数a,代表n对2取余的余数。
若(n<2)
则为递归出口,输出a。
否则
递归公式,dectobin(n/2)
输出a。
2.代码截图

3.调试问题
- 一开始对递归函数的位置与输出的位置放的不对。
解决方法:改变位置,先进入递归再输出。
二、学生成绩管理系统
1.画函数模块图,简要介绍函数功能。
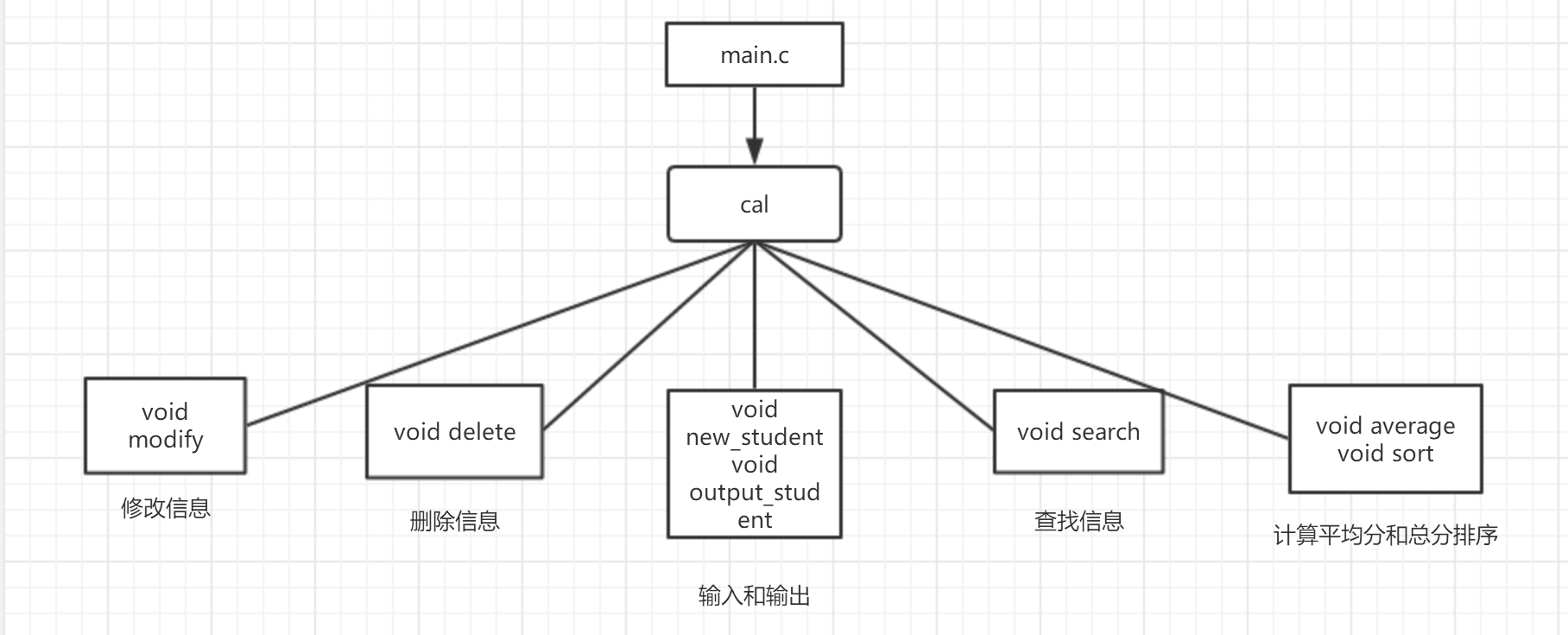
2.截图展示你的工程文件
3.函数代码部分截图
main.c
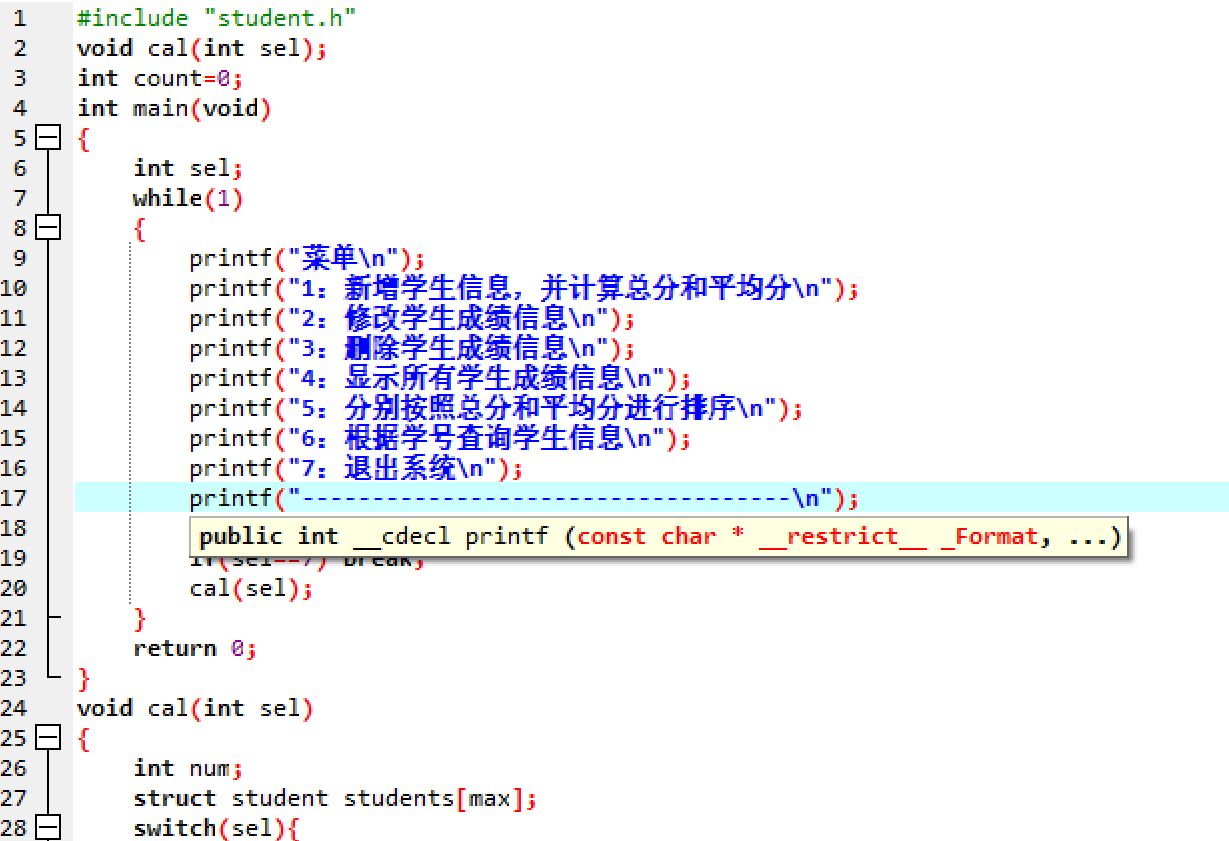
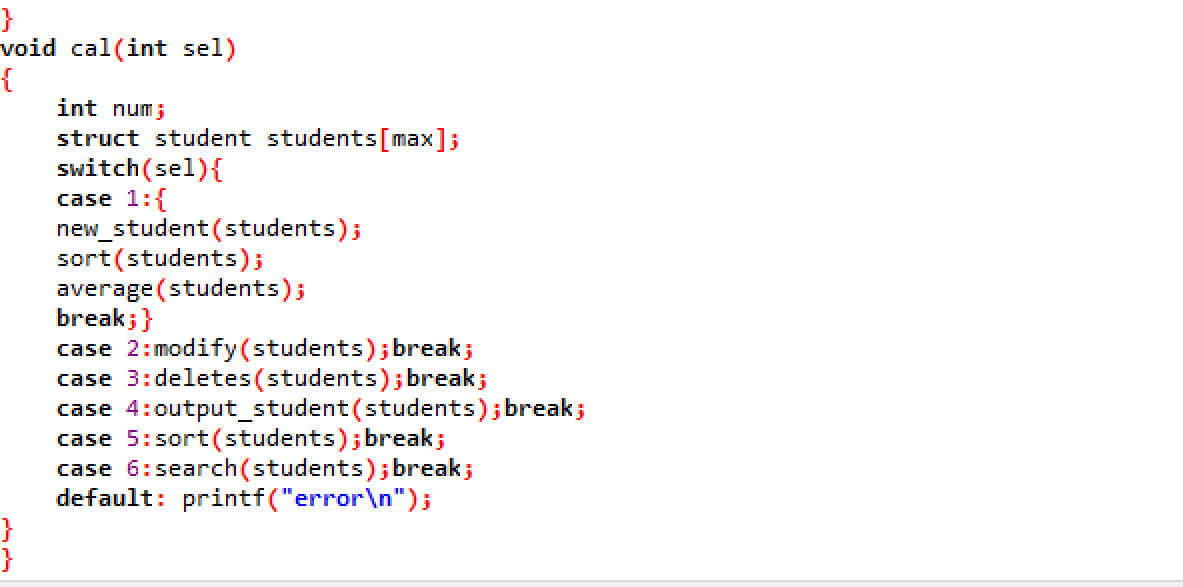
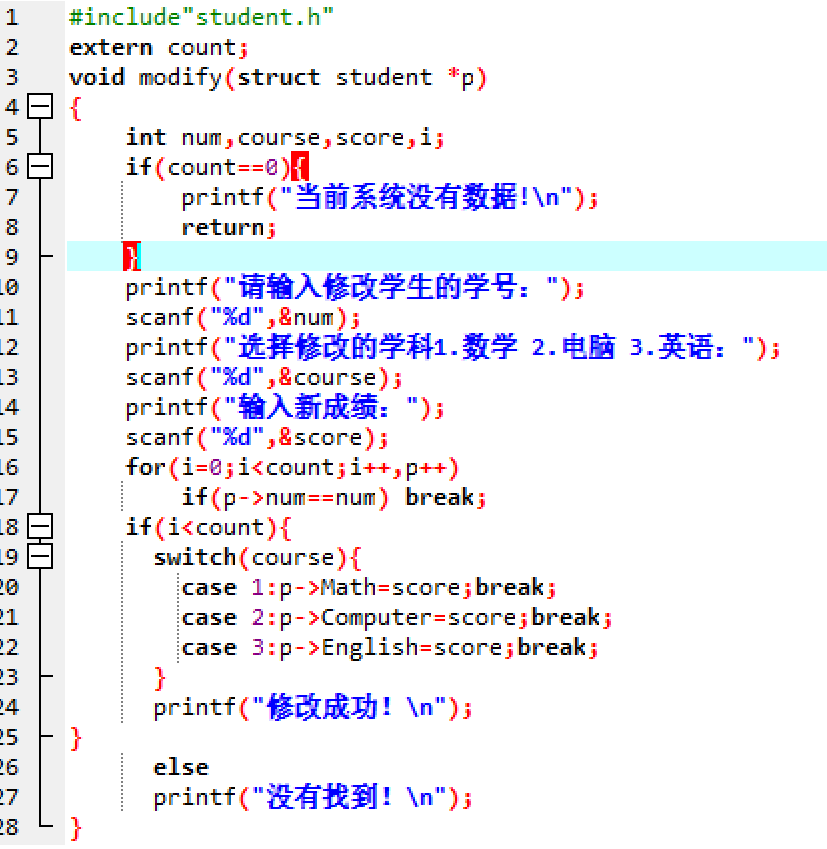
modify.c
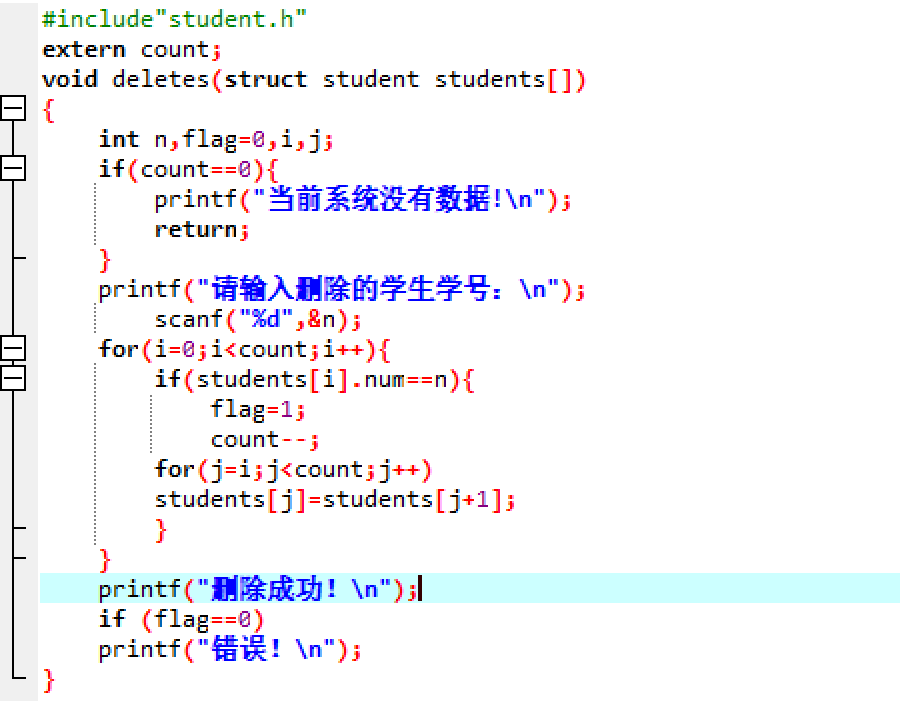
delete.c
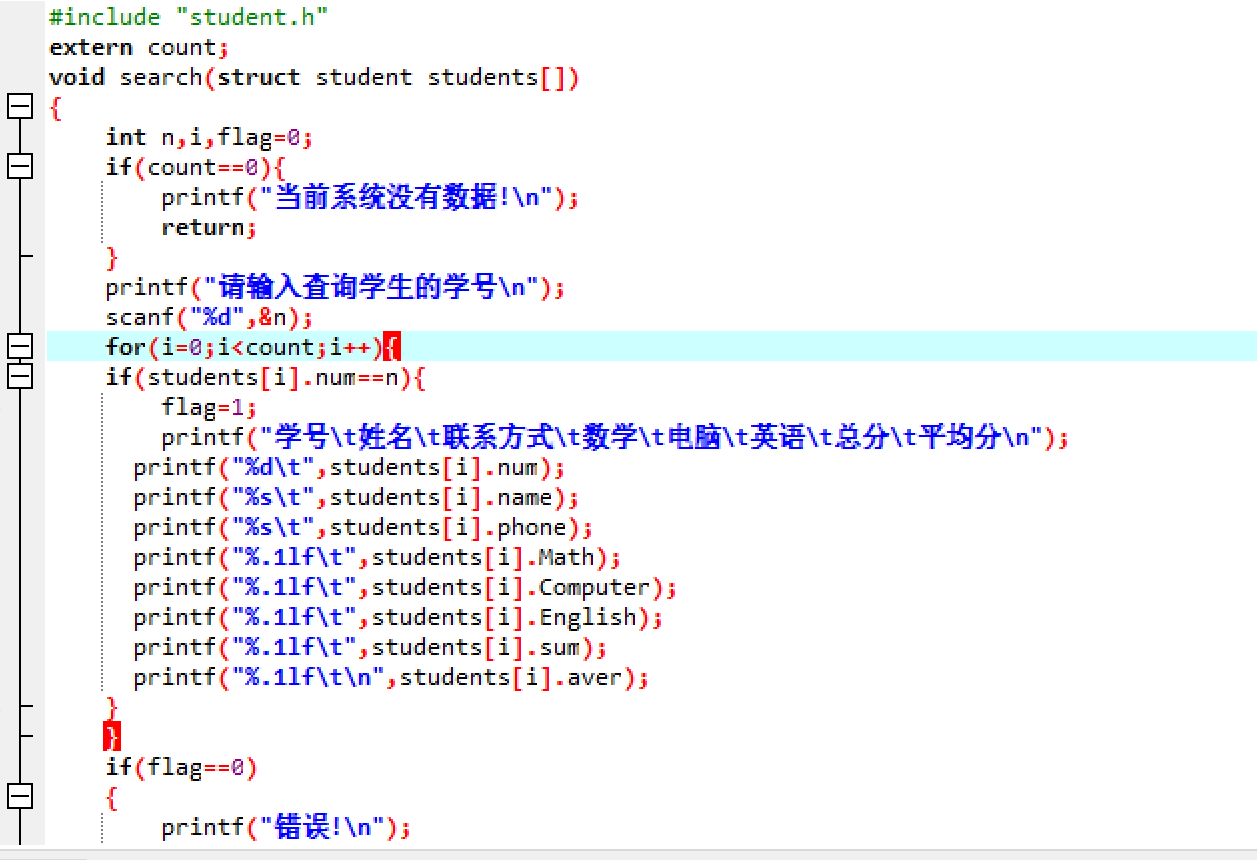
search.c
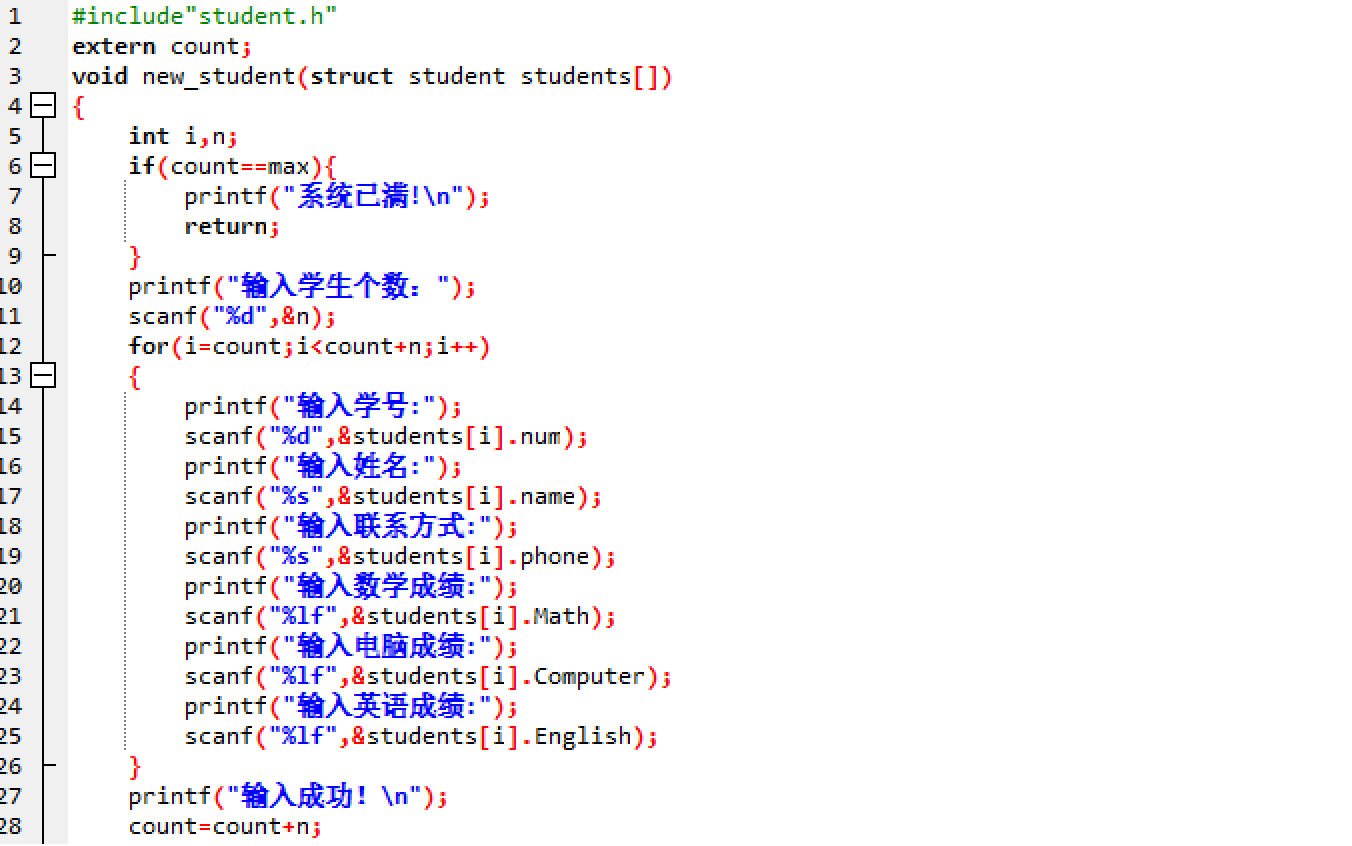
input_output.c
aver_sort.c
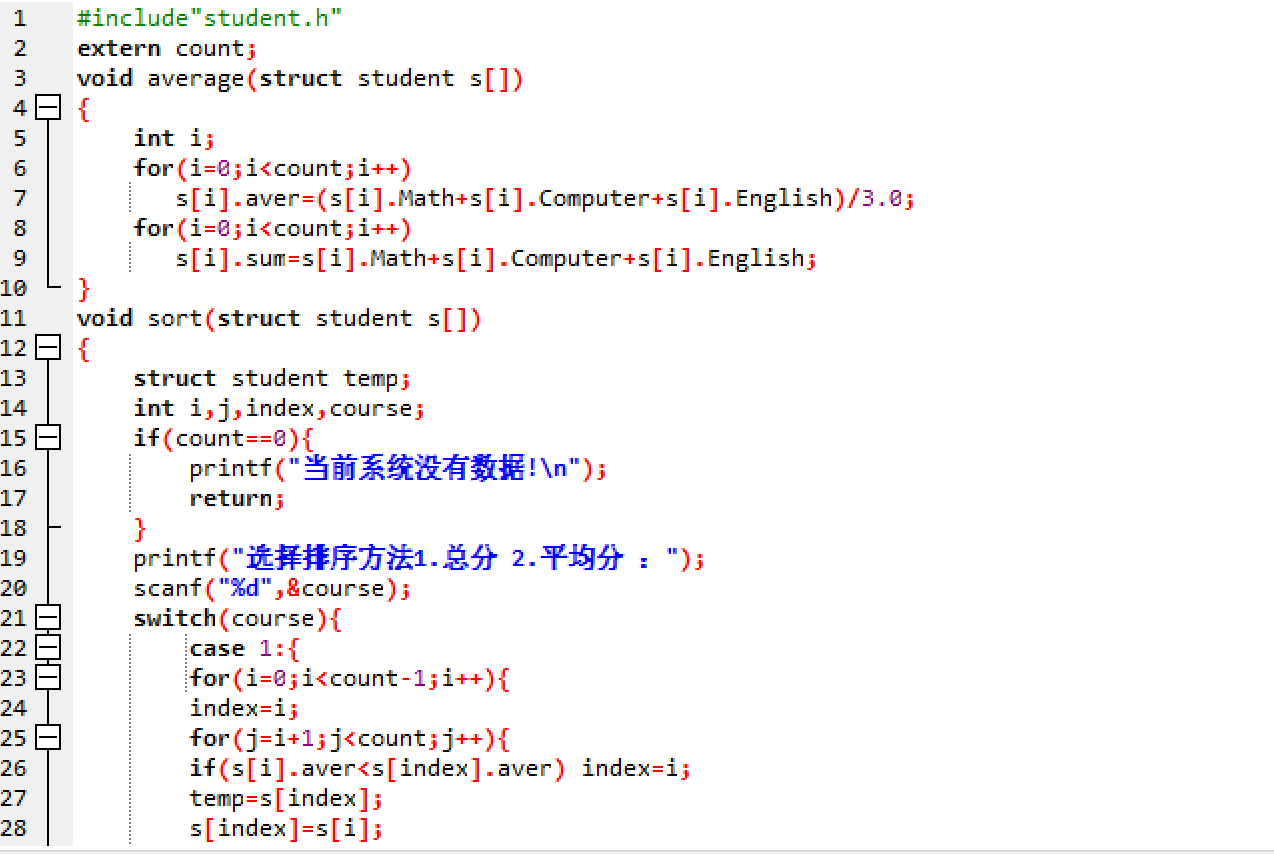
- 本系统代码总行数:250
4.调试结果展示
输入
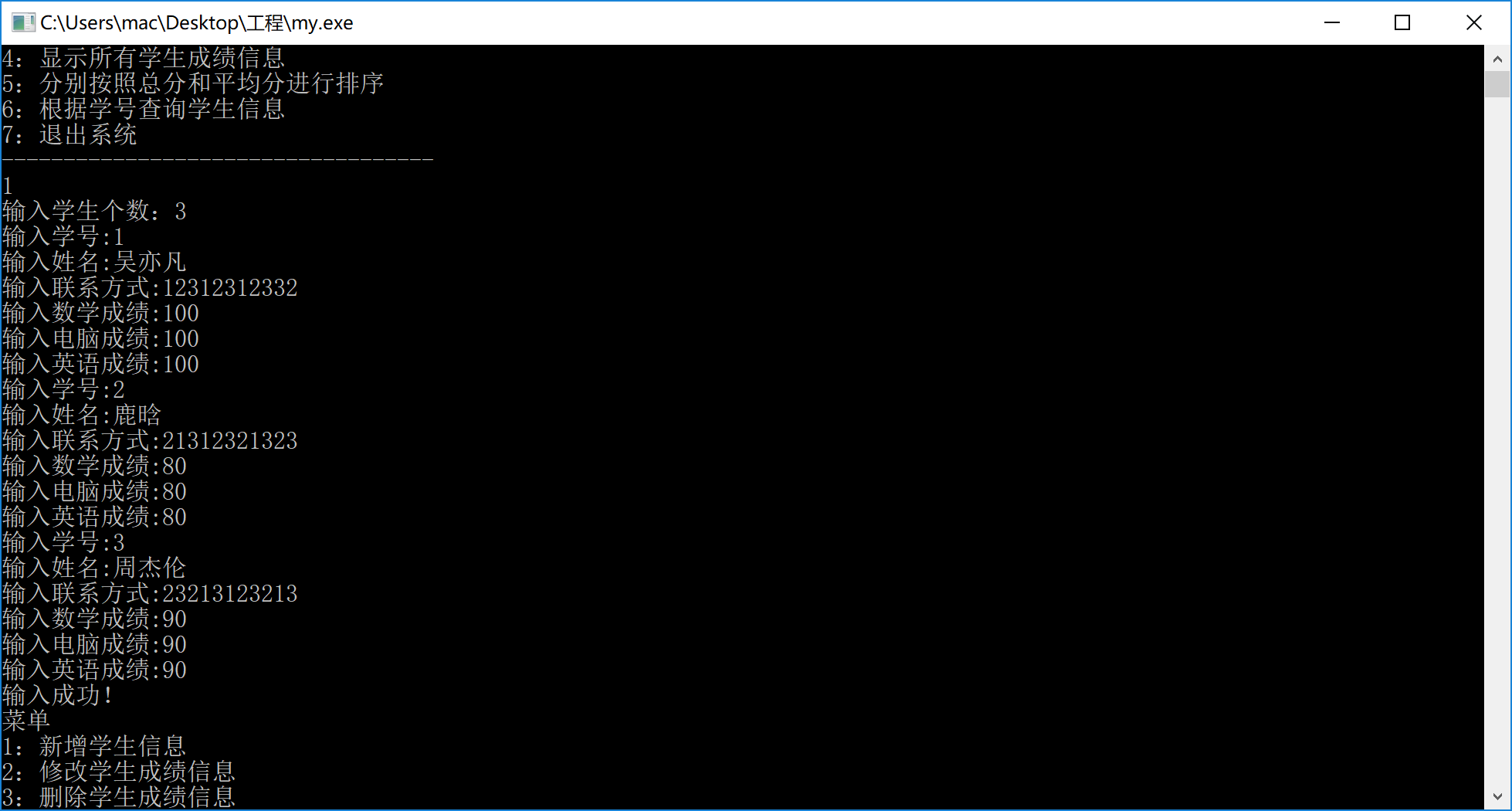
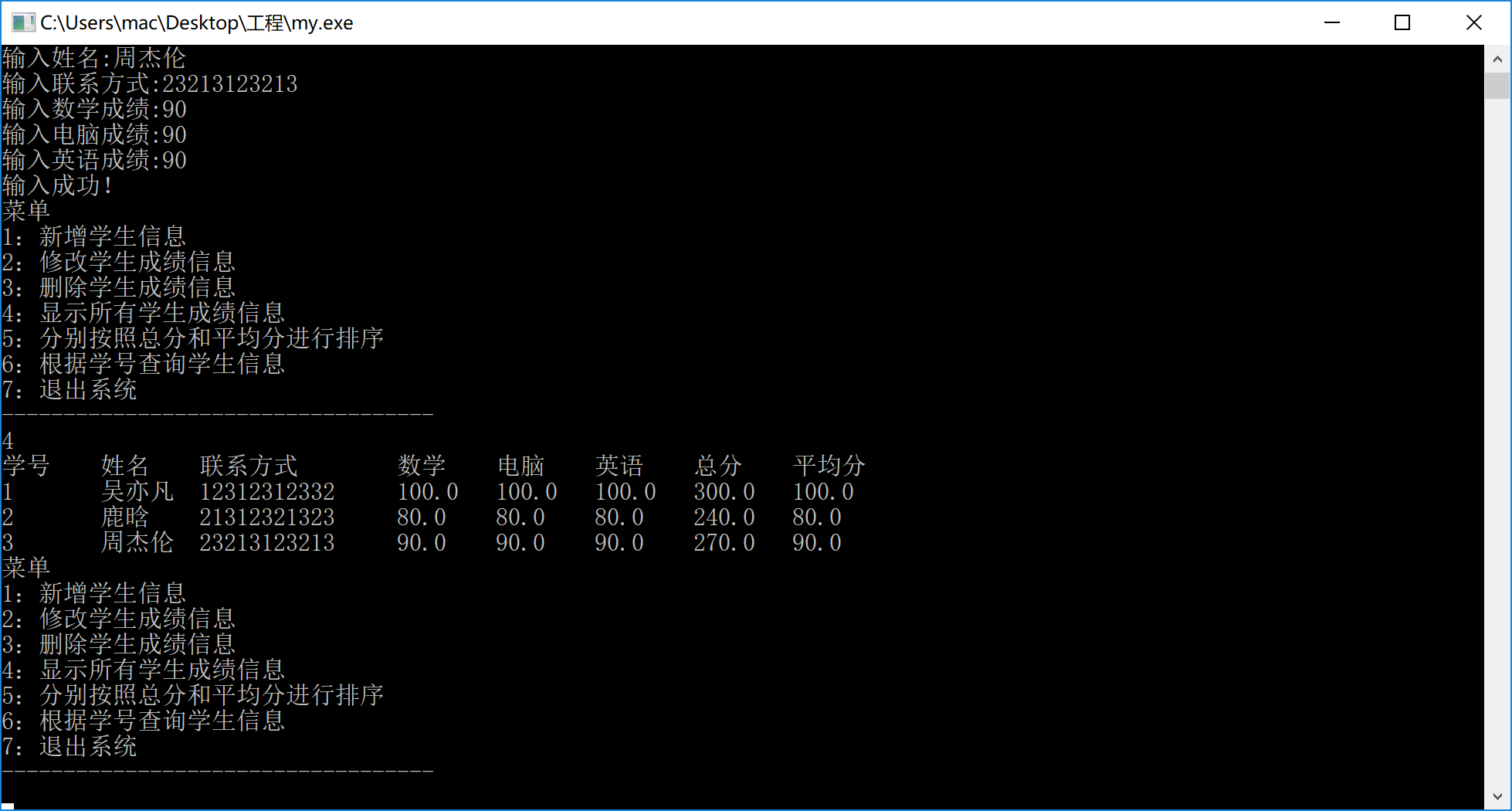
显示
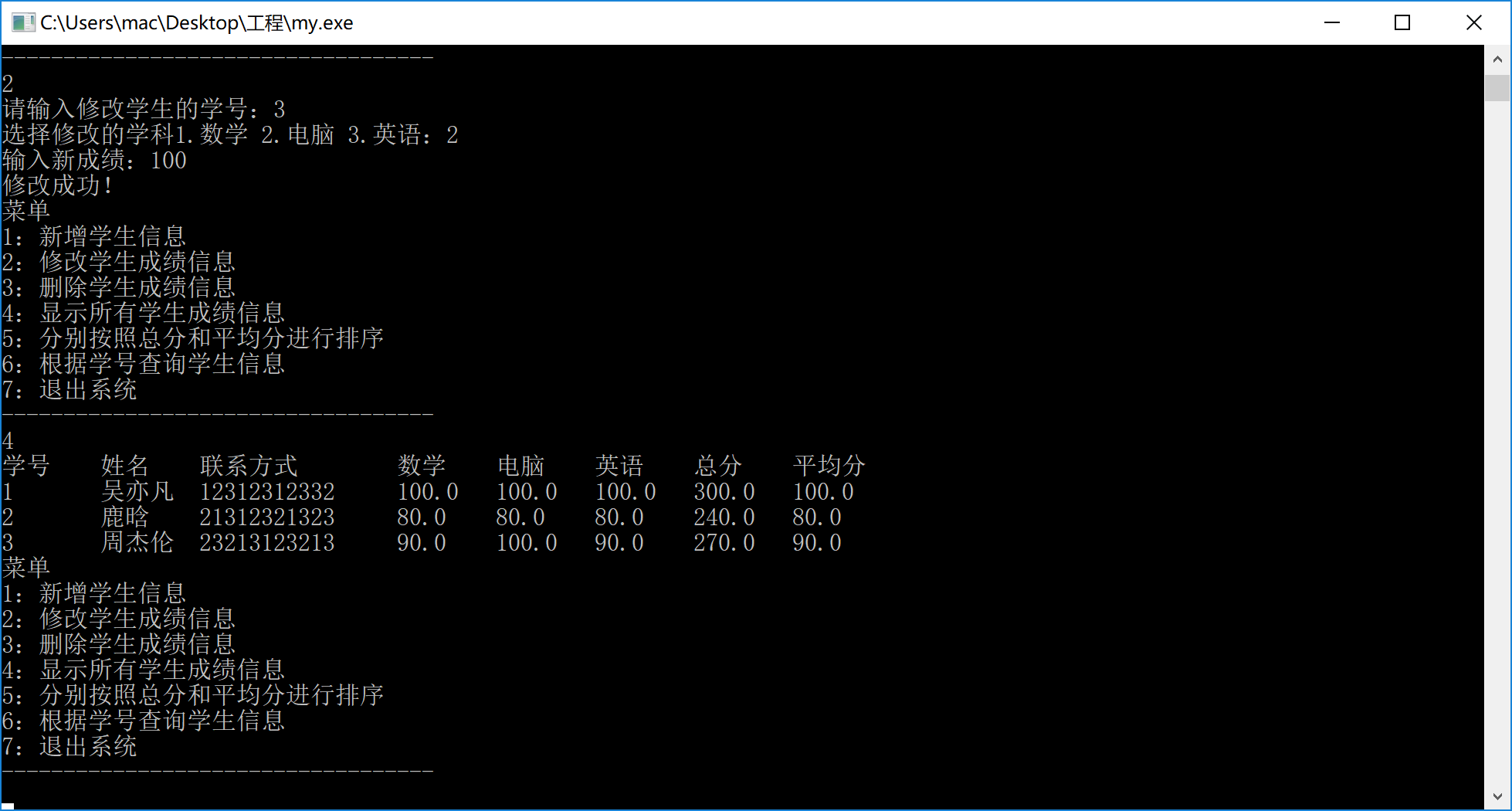
修改成绩
根据学号查询学生信息
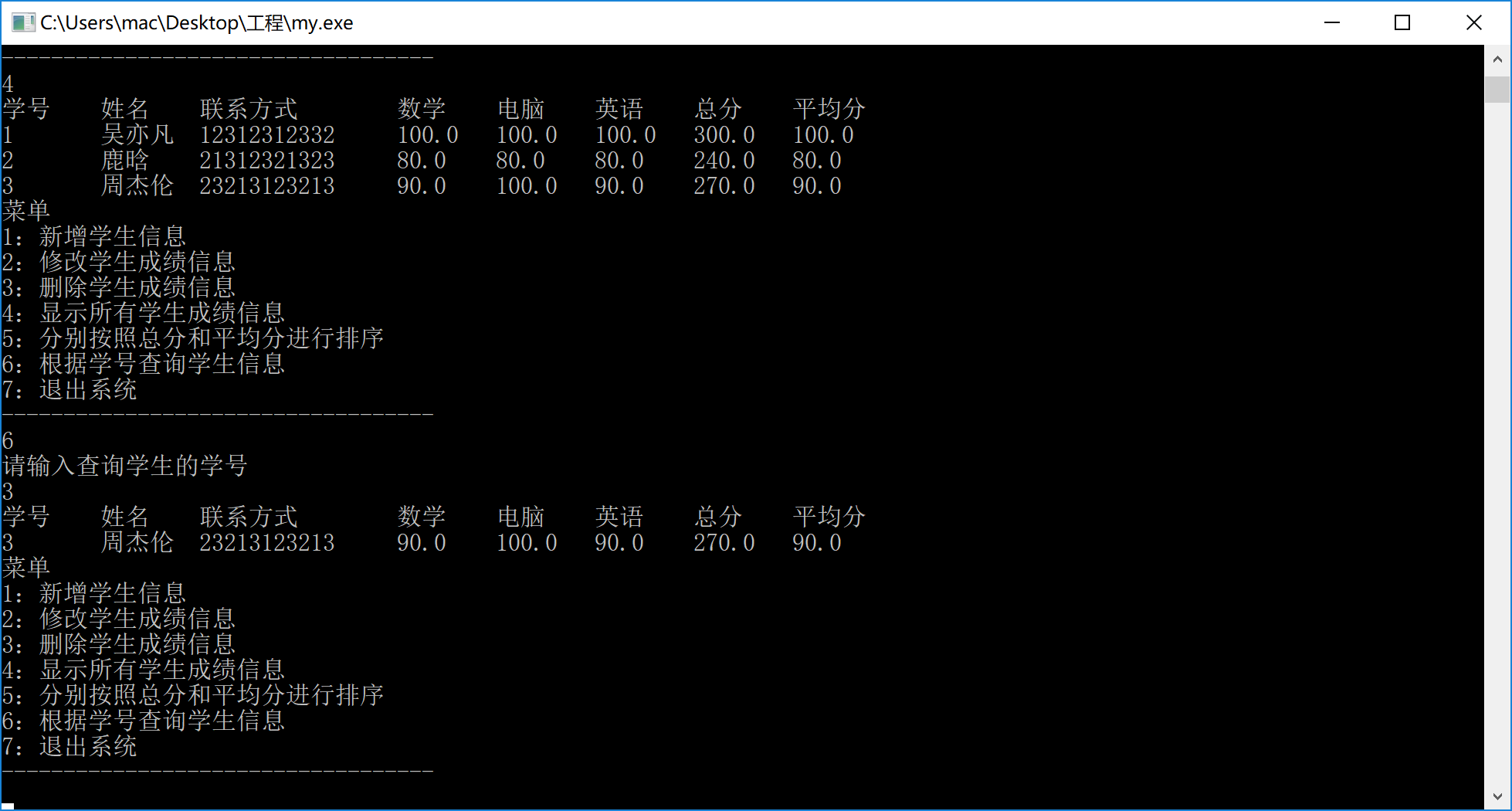
删除学生信息
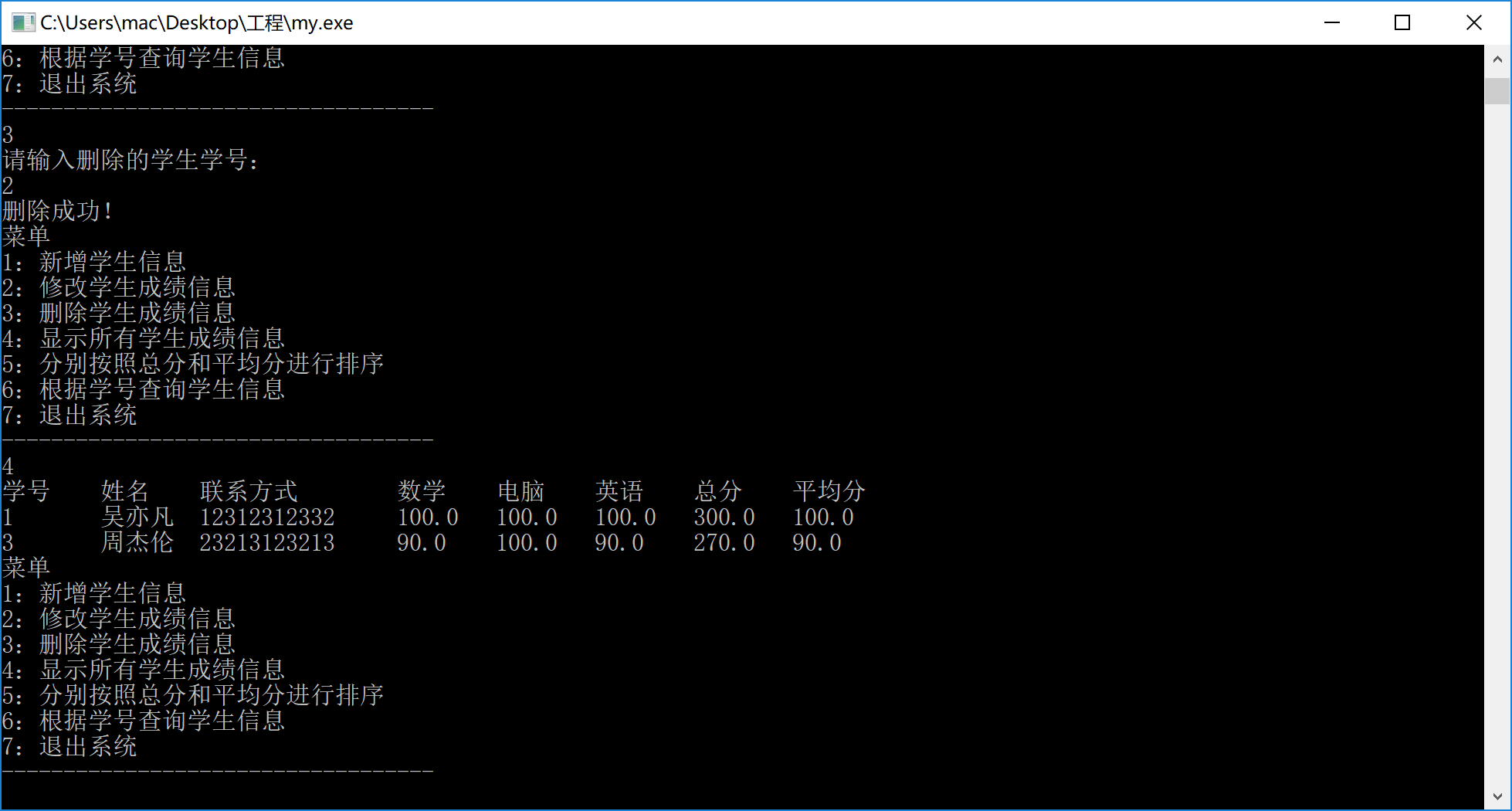
5.调试碰到问题及解决办法
- 1.在创建工程的过程中由于工程建立的不当已经过多的c文件互相影响导致工程无法运行。
解决方法:询求老师帮助,建立了基本的工程。 - 2.新建信息一开始i=0,导致创建新信息之后之前的信息就会消失。
解决方法:将i=0改为i=count,i<count+n。 - 3.排序功能和按学号排序还未完善。
- 4.对于一些非法输入还未健全判断方法,以及系统的交互还不够友好,操作失误就要重新输入。
三、截图本周题目集的PTA最后排名。

四、阅读代码
写一个计算斐波那契数列的通项f(n),已知f1=1,f2=1,以后每项都是前两项的和。
template <typename T>
T f(T n) //递归函数
{
if (n == 1 || n == 2)
{
return 1;
}
else
{
return f(n - 1) + f(n - 2);
}
}
int _tmain(int argc, _TCHAR* argv[])
{
int n;
cout << "Please input n:" << endl;
cin >> n;
cout << "n! = " << f(n) << endl;
return 0;
}
本题通过递归函数计算斐波那契数列,有了递归的算法, 用程序实现实在再简单不过了,很直观的表示出了各个通项之间的关系,不仅简洁而且不会出错。如果使用正常的函数写法会使代码量增加。递归虽然较为难以理解,但很多东西用递归却更加简单,这就是递归的重要之处。
五、本周学习总结
1.介绍本周学习内容
- 1.学会了基本的函数嵌套调用,懂得如何模块化使得代码可读性增强,实现复杂问题结构化程序。
- 2.递归函数中递归出口和递归式子是要点,掌握式子的关系即可不要深究过程,不然会混乱。
- 3.宏定义格式 #define 宏名 宏定义字符串
宏还能实现简单的函数功能。宏替换不做计算,只做替换。 - 4.一个程序中只允有一个主模块,为了能调用写在其他文件模块中的函数,可以使用文件包含。
全局变量只能在某个模块中定义一次,如果其他模块需要则需要通过外部变量声明 etern 变量名表。
2.学习体会
- 本周的学习内容很多,也相对的复杂和零碎,在学习上有一定的困难,特别是递归函数和工程,无法快速的理解。c语言的一些基础概念和知识容易忽略或者混淆,接下来还是会认真的阅读书本和相关的代码,梳理其中的内容。