Introduction
(1)背景知识:
① 人脸识别是具有高可靠性的生物识别技术,但在低解析度(resolution)和姿态变化下效果很差.
② 步态(gait)是全身行为的生物识别特征,大部分步态识别方法是基于轮廓而不受外貌影响,但在复杂的背景和遮挡下轮廓难以提取.
(2)问题场景:
假设行人在不同的相机中不更换衣服,结合人体外貌特征和步态特征进行识别.
难点:行人重识别受到姿态、视角、光照、遮挡的影响,空间对齐(spatial alignment)通过处理不同部位的样貌来解决该问题. 然而人体部位在不同阶段也有变化,如游泳时手臂样貌会变化,且会遮挡躯干等.
(3)本文工作:
提出了一个时空表示方法,对人体部位空间布局和动作原语(action primitive)的时间序列进行编码(关注的重点在于“行走”,忽略了其余动作),具体来说:
对于一个视频序列,裁剪成若干步行周期. 在时间上,将步行周期分割成不同的动作阶段;在空间上,将不同的身体部位按姿态划分. 由此得到众多的视频标记点(video blobs),每一个标记点对应一个动作原语,也称为人体动作单元(body-action unit).
从body-action units中提取出Fisher vectors(一种广义的Bag-of-Words类型的特征),由此构建出特征向量对行人的样貌进行表示.
(什么是BoW特征?【传送门】)
Proposed Method

(1)时空人体动作模型(Spatio-Temporal Body-Action Model)
① 提取步行周期:
对于一个视频 Q = (I1, I2, ..., It),每一帧 I 的运动能量强度计算为:
![]()
由于通常行人的下半身运动最突出和连续,U 是图片的下半部分的像素集,vx 和 vy 是水平和竖直方向上的 optic flow. (什么是optic flow?)
流动能量分布(Flow Energy Profile, FEP):E = (e1, e2, ..., et).
当 E 最大时,对应两腿重合的情况;当 E 最小时,对应两腿分开最远的情况.
但是没有规格化的 FEP 噪声比较大,需要通过离散傅里叶变化进行规格化,如上图的(b).
(离散傅里叶变化如何工作?)
每一个步行周期包含2段正弦曲线,即每条腿走一步是一段曲线.
将一个步行周期截取成更小的段(segments),对应不同的动作原语,S = (s1, s2, ..., sN).
② 确定Body-Action Unit:
将人体分为6部分:P = (p1, p2, ..., pM),pi 是某一帧上的一个区域,其中 M 设置为6.
结合在①中得出的步行周期的动作原语,得到规格为 M*N 的Body-Action Units,即人体的6个部位在步行的4个阶段不同的动作,定义如下:
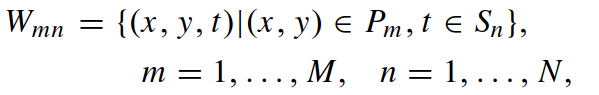
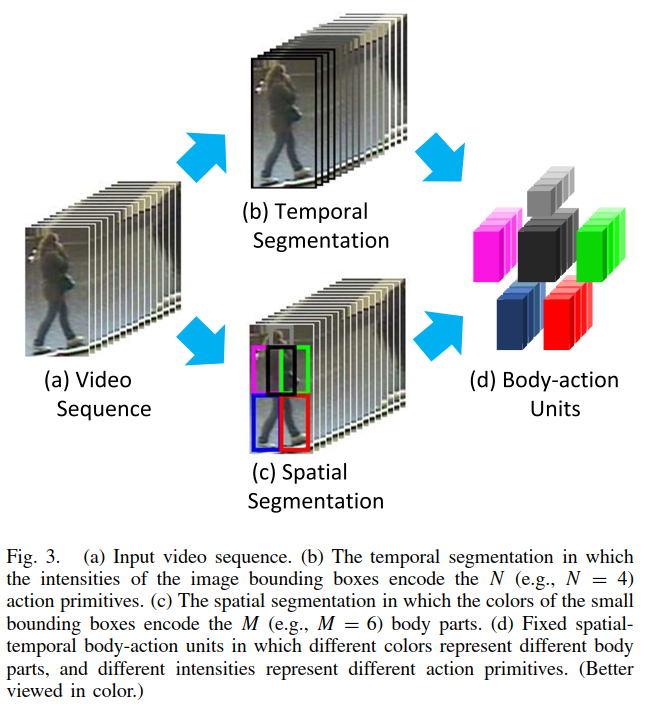
③ 自适应人体动作单元(adaptive Body-Action Units):
由于步行的动态性,识别的人体部位可能不准确,比如两只腿可能会重叠,如下图:

解决方法:对模板进行改进,分为两种:基于插值函数(interpolation function)和基于越阶函数(step function),调整后的结果如下图:
个人理解:前者的模板框是连续变换的,后者是离散变换的.

效果如下图:interpolation function 是逐渐变化,而 step function 的变化形式单一.

(2)Fisher vector的学习与提取:
特征构成:
![]()
其中 x~, y~, t~ 表示在这个unit中的像素点相对坐标,I(x,y,t) 为像素强度,由于图片有3个通道,因此 I 和它的偏导均为3维,每个像素点的特征总维数为 D = 3 + 7*3 = 24.
利用训练集得出 W,并提取出相应的特征,训练出GMM(高斯混合模型).
什么是高斯混合模型?【传送门】
训练得到的模型构成:![]() ,K设置为32.
,K设置为32.
μk、σk、πk 分别表示均值、协方差、高斯成分的先验概率(prior probability).
高斯成分(Gaussian component):
![]()
计算第 i 个像素特征描述的第 k 个高斯成分的后验概率为:
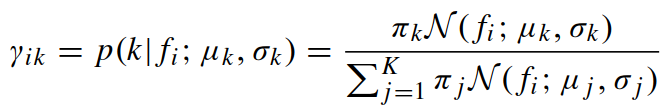
Fisher vector由wk、uk、vk 构成(其中 w 为标量,u 和 v 是向量),即 Θ(W) = [w1, u1, v1, ..., wK, uK, vK],计算如下:
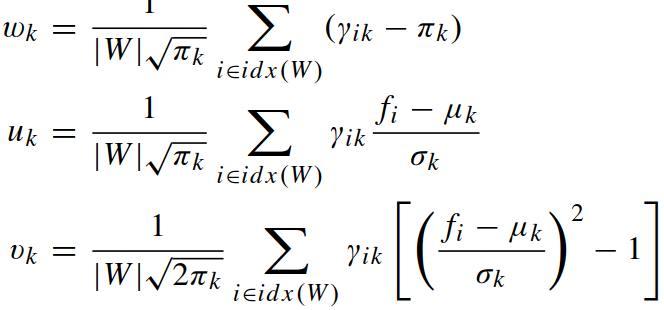
一段视频含有若干步行周期,对于任意一个周期,划分为 N 个动作原语,M 个人体动作部位,使用的GMM由 K 个高斯成分构成,每帧每部位的每个高斯成分有 2D+1 个特征构成,由此得出Fisher vector的维度是:(2D+1)KMN.
(w、u、v三个量的意义是什么?)
(3)结合监督学习:
结合样貌表征和监督距离矩阵,如KISSME.
KISSME简介:
查询集中的行人 x,有 nx 个特征 xi(i = 1, ..., nx);
视频库中的行人 y,有 ny 个特征 yj(j = 1, ..., ny).
特征的差记为 dij = xi - yj.
d 的行人内(intrapersonal)协方差矩阵为 ΣI, 行人间(extrapersonal)协方差矩阵 ΣE.
两个向量之比的对数为:![]()
实验中的两个协方差矩阵可以估算为:
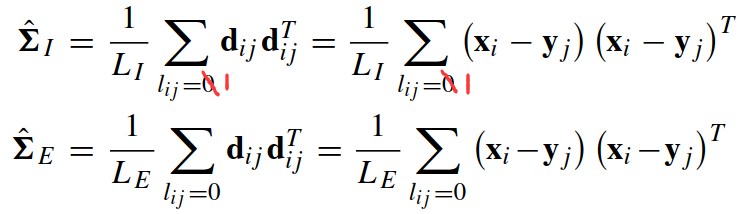
其中 lij = 1表示 xi 和 xj 属于同一个人,lij = 0表示 xi 和 xj 不属于同一个人. LI 和 LE 分别是相同特征对和不同特征对的数量.(感觉上面公式出错了,1写成了0)
KISSME度量矩阵 ψ 为:![]() ,使得满足如下条件(第二个距离公式比第一个效果更好):
,使得满足如下条件(第二个距离公式比第一个效果更好):
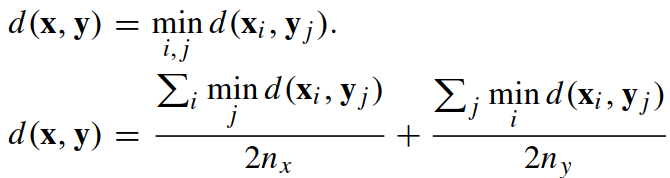
其中:![]()
(KISSME怎么理解?)
(4)方法概览:
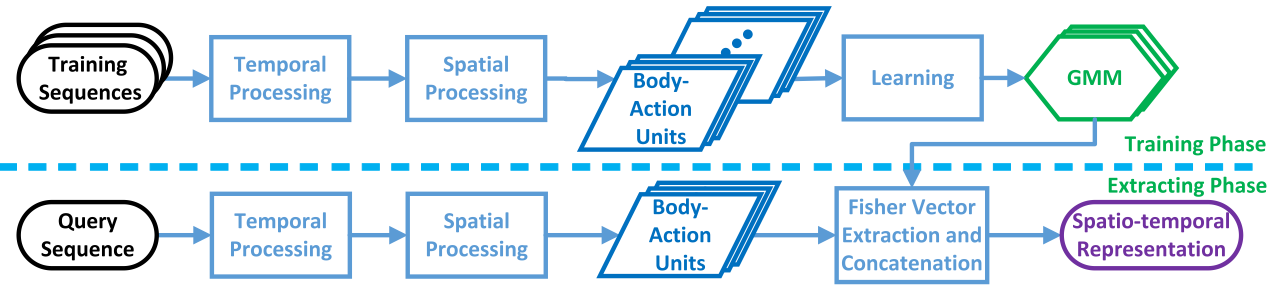
Experiments
(1)数据集和实验设置:
① 数据集:iLIDS-VID、PRID2011、SDU-VID(新引入)
iLIDS-VID、PRID2011的介绍在【前文】中介绍过;
SDU-VID数据集包含了300个行人的600个图像序列,每个序列包含16-346帧,平均130帧.
【数据集链接】
② 实验设置:
M = 6
N = 4
K = 32
由于不同的视频序列含有不同数量的步行周期,每一个周期提取出特征后,选用距离最近的来表示.(这段话没有理解作者确切的意思,暂且这么理解)
实验使用了24维和12维特征,24维是上文中 f 所提特征,12维是删去了颜色和二阶导数的特征.
(2)实验结果:
(实验结果的分析看得不是很明白,略过)