基础算法总结
对于算法总结,在证明等方面不做深究(大多数还未深刻理解),主要记录:结论,使用条件,适用问题等,并附上一些总结的较好的博主的博客。由于内容较多,时间少,先罗列清单,慢慢补上。
数学
Lucas定理(用于m,n较大时,求C(m,n)%P)
Miller Robin算法(大素数判定)
欧拉函数(求不大于n且与n互质的数的个数)、费马小定理、欧拉定理(用于求逆元)
扩展欧几里得算法(用于解二元一次方程,求逆元等)
欧拉降幂公式(用于b较大时,求a^b%mod):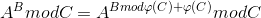
康拓展开(求全排列中的位次)
容斥原理(用于计数)
划分数
离散化
矩阵快速幂
博弈论
Bash博弈
Nim博弈
Wythoff博弈
Fibonacci博弈
SG函数
字符串
KMP算法(字符串匹配)
Manancher算法(最大回文串)
AC自动机(多模匹配)
字典树
图论
带权并查集
Dijkstra最短路
Bellman-Ford最短路
Tarjan算法(求强连通分量)
二分图(关于其若干性质)
匈牙利算法(二分图匹配)
LCA(最近公共祖先的若干算法)
数据结构
线段树
树状数组
主席树
Treap
动态规划
背包模型DP
数位DP
区间DP
树形DP
零碎技巧或结论
快速乘(O(1))
手动扩栈
读入/输出优化
LIS(O(nlogn))
LICS(O(nm))
工具
随机数生成对拍
JAVA实现高精