欧拉函数
欧拉函数求的是小于n且与n互质的数的个数。
以下给出一些欧拉函数的性质:
① 当m,n互质时,有phi(m*n)= phi(m)*phi(n);
② 若i%p==0,有phi(i*p) = p * phi(i);
③ 对于互质x与p,有x^phi(p)≡1(mod p),因此x的逆元为x^(phi(p)-1),即欧拉定理。
(特别地,当p为质数时,phi(p)=p-1,此时逆元为x^(p-2),即费马小定理)
④ 当n为奇数时,phi(2n)=phi(n)
⑤ 若x与p互质,则p-x也与p互质,因此小于p且与p互质的数之和为phi(x)*x/2;
###求x的欧拉函数
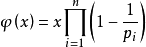
由此公式可得:
```C++
ll phi(ll n)
{
ll res=n;
for (int i=2;i*i<=n;++i)
{
if (n%i==0)
res=res/i*(i-1);
while (n%i==0)
n/=i;
}
if (n>1)
res=res/n*(n-1);
return res;
}
```
根据之前提到的性质还可以线性打欧拉函数表
```C++
ll phi[maxn],prime[maxn];
bool sign[maxn];
void phi_init()
{
int cnt=0;
phi[1]=1;
for (int i=2;i