zoukankan      html  css  js  c++  java

  • [FJOI2018]所罗门王的宝藏【差分约束】

    题目描述

    据古代传说记载，所罗门王既是智慧的代表，又是财富的象征。他建立了强大而富有的国家，聚集了大批的黄金象牙和钻石，并把这些价值连城的珍宝藏在一个神秘的地方，这就是世人瞩目的“所罗门王的宝藏”。多少个世纪以来，人们一直在寻找这批早已失落的古代文明宝藏，寻找盛产黄金和钻石的宝地。曾经追寻所罗门王宝藏的冒险者们都一去不回，至今没人解开这个谜题。亨利男爵在一次幸运的旅途中意外地得到了三百年前一位葡萄牙贵族留下的写在羊皮卷上的所罗门王的藏宝图和一本寻宝秘籍。在这张藏宝图的诱惑下，亨利男爵邀请约翰上校和勇敢的猎象人夸特曼开始了寻找埋葬在黑暗地底的所罗门王宝藏的艰险历程。他们横穿渺无边际的沙漠和浓荫蔽日的原始森林，越过汹涌澎湃的激流险滩，翻越高耸入云的峻岭雪山，饱尝沙漠的酷热和冰雪严寒，在藏宝图的指引下来到非洲一个原始的神秘国度库库安纳。这里有残酷的人殉制度，有一个拥有一千个妻室的独眼暴君特瓦拉，有像兀鹫一般丑恶诡诈老而不死的女巫加古尔，还有美丽聪慧的绝代佳人弗拉塔。在这片陌生而又险象环生的土地上三位寻宝英雄历尽艰辛，终于在绝代佳人弗拉塔的帮助下在海底深处找到了珍藏这批价值连城宝藏的巨大的藏宝洞。然而在女巫加古尔的精心策划下，一场灭顶之灾正在悄悄逼近。

    藏宝洞的洞门十分坚固且洞门紧闭，如果不知道开启洞门的秘密是无法打开藏宝洞的洞门。在藏宝洞的洞门一侧有一个奇怪的矩形密码阵列。根据寻宝秘籍的记载，在密码阵列每行的左侧和每列的顶端都有一颗红宝石按钮。每个按钮都可以向左或向右转动。每向左转动一次按钮，相应的行或列中数字都增 11。每向右转动一次按钮，相应的行或列中数字都减 11。在矩形密码阵列的若干特定位置镶嵌着绿宝石。只有当所有绿宝石位置的数字与藏宝图记载的密码完全相同，紧闭的洞门就会自动缓缓打开。女巫加古尔早已得知开门的秘密。为了阻止寻宝者打开洞门，女巫加古尔为开门的密码阵列设置了全 00 的初始状态。试图打开洞门的寻宝者如果不能迅速转动按钮使所有绿宝石位置的数字与藏宝图记载的密码完全相同，就会自动启动藏宝洞玄妙的暗器机关，使寻宝者遭到灭顶攻击而死于非命。

    您能帮助三位寻宝英雄顺利打开藏宝洞的洞门吗？

    编程任务：对于给定的密码阵列，找到获得正确密码的红宝石按钮的转动序列。

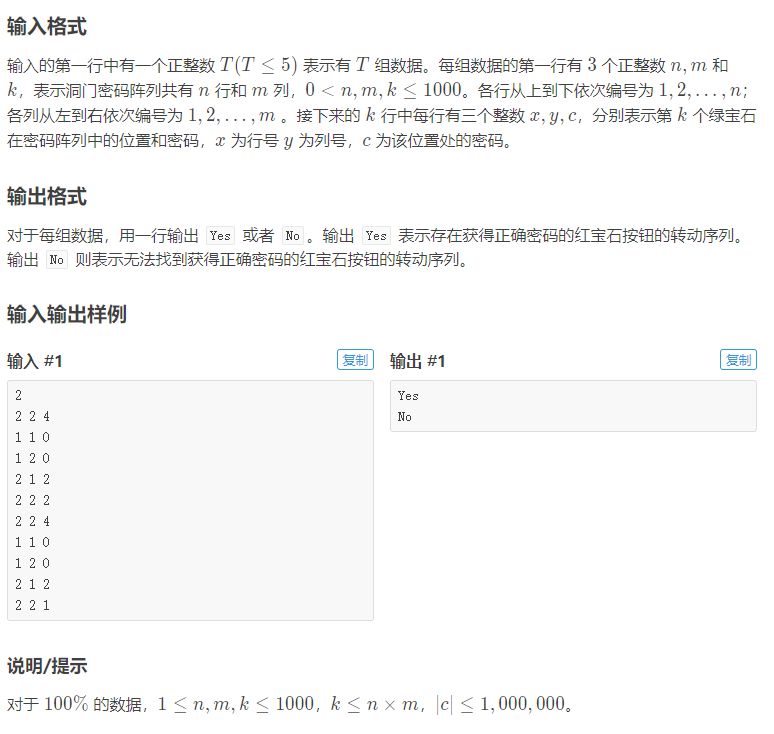
     思路

    　　把点 Ai,j 拆成表示此行加过多少次、此列减过多少次两个点

    　　最后要得到的即为 line[Ai,j] - row[Ai,j] = C

    　　即为 line[Ai,j] - row[Ai,j] ≥ C

    　　　　 line[Ai,j] - row[Ai,j] ≤ C

    　　此方程组有解

    　　则只当差分约束系统无解时不能解开谜题

    　　如何判断差分约束系统是否有解

    　　当且仅当松弛时出现负环时无解

    　　差分约束知识详见：https://www.cnblogs.com/zzz-hhh/p/11200893.html

    CODE

      1 #include <bits/stdc++.h>
  2 #define dbg(x) cout << #x << "=" << x << endl
  3 #define eps 1e-8
  4 #define pi acos(-1.0)
  5 
  6 using namespace std;
  7 typedef long long LL;
  8 
  9 template<class T>inline void read(T &res)
 10 {
 11     char c;T flag=1;
 12     while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;res=c-'0';
 13     while((c=getchar())>='0'&&c<='9')res=res*10+c-'0';res*=flag;
 14 }
 15 
 16 namespace _buff {
 17     const size_t BUFF = 1 << 19;
 18     char ibuf[BUFF], *ib = ibuf, *ie = ibuf;
 19     char getc() {
 20         if (ib == ie) {
 21             ib = ibuf;
 22             ie = ibuf + fread(ibuf, 1, BUFF, stdin);
 23         }
 24         return ib == ie ? -1 : *ib++;
 25     }
 26 }
 27 
 28 int qread() {
 29     using namespace _buff;
 30     int ret = 0;
 31     bool pos = true;
 32     char c = getc();
 33     for (; (c < '0' || c > '9') && c != '-'; c = getc()) {
 34         assert(~c);
 35     }
 36     if (c == '-') {
 37         pos = false;
 38         c = getc();
 39     }
 40     for (; c >= '0' && c <= '9'; c = getc()) {
 41         ret = (ret << 3) + (ret << 1) + (c ^ 48);
 42     }
 43     return pos ? ret : -ret;
 44 }
 45 
 46 const int maxn = 1e4 + 7;
 47 const int inf = 0x3f3f3f3f;
 48 
 49 int n,m;
 50 
 51 int head[maxn << 1], edge[maxn << 1], nxt[maxn << 1];
 52 int c[maxn << 1];
 53 int cnt;
 54 int dis[maxn], in[maxn];
 55 bool vis[maxn];
 56 
 57 void BuildGraph(int u, int v, int w) {
 58     cnt++;
 59     edge[cnt] = v;
 60     nxt[cnt] = head[u];
 61     c[cnt] = w;
 62     head[u] = cnt;
 63 }
 64 
 65 bool spfa(int u) {
 66     //memset(dis, -1, sizeof(dis));
 67     for ( int i = 1; i <= n + m; ++i ) {
 68         in[i] = 0, vis[i] = 0;
 69         dis[i] = inf;
 70     }
 71     //vis[u] = 1;
 72     dis[u] = 0;
 73     in[u] = 1;
 74     queue <int> q;
 75     q.push(u); 
 76     while(!q.empty()) {
 77         u = q.front();
 78         q.pop();
 79         vis[u] = 0;
 80         for (int i = head[u]; i ; i = nxt[i]) {
 81             int v = edge[i];
 82             int w = c[i];
 83             if(dis[v] > dis[u] + w) {
 84                 if(in[v] >= n + m) {
 85                     return true;
 86                 }
 87                 dis[v] = dis[u] + w;
 88                 if(!vis[v]) {
 89                     q.push(v);
 90                     vis[v] = 1;
 91                     ++in[v];
 92                 }
 93             }
 94         }
 95     }
 96     return false;
 97 }
 98 
 99 int t;
100 
101 int main()
102 {
103     read(t);
104     while(t--) {
105         int k;
106         read(n); read(m); read(k);
107         memset(head, 0, sizeof(head));
108         cnt = 0;
109         int s = n + m + 1;
110         for ( int i = 1; i <= n + m; ++i ) {
111             BuildGraph(s, i, 0);
112         }
113         for ( int i = 1; i <= k; ++i ) {
114             int x, y, c;
115             read(x); read(y); read(c);
116             BuildGraph(x, y + n, c);
117             BuildGraph(y + n, x, -c);
118         }
119         if(spfa(s)) {
120             puts("No");
121         }
122         else {
123             puts("Yes");
124         }
125     }
126     return 0;
127 }
    View Code
    #include <bits/stdc++.h>
    #define dbg(x) cout << #x << "=" << x << endl
    #define eps 1e-8
    #define pi acos(-1.0)

    using namespace std;
    typedef long long LL;

    template<class T>inline void read(T &res)
    {
        char c;T flag=1;
        while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;res=c-'0';
        while((c=getchar())>='0'&&c<='9')res=res*10+c-'0';res*=flag;
    }

    namespace _buff {
        const size_t BUFF = 1 << 19;
        char ibuf[BUFF], *ib = ibuf, *ie = ibuf;
        char getc() {
            if (ib == ie) {
                ib = ibuf;
                ie = ibuf + fread(ibuf, 1, BUFF, stdin);
            }
            return ib == ie ? -1 : *ib++;
        }
    }

    int qread() {
        using namespace _buff;
        int ret = 0;
        bool pos = true;
        char c = getc();
        for (; (c < '0' || c > '9') && c != '-'; c = getc()) {
            assert(~c);
        }
        if (c == '-') {
            pos = false;
            c = getc();
        }
        for (; c >= '0' && c <= '9'; c = getc()) {
            ret = (ret << 3) + (ret << 1) + (c ^ 48);
        }
        return pos ? ret : -ret;
    }

    const int maxn = 1e4 + 7;
    const int inf = 0x3f3f3f3f;

    int n,m;

    int head[maxn << 1], edge[maxn << 1], nxt[maxn << 1];
    int c[maxn << 1];
    int cnt;
    int dis[maxn], in[maxn];
    bool vis[maxn];

    void BuildGraph(int u, int v, int w) {
        cnt++;
        edge[cnt] = v;
        nxt[cnt] = head[u];
        c[cnt] = w;
        head[u] = cnt;
    }

    bool spfa(int u) {
        //memset(dis, -1, sizeof(dis));
        for ( int i = 1; i <= n + m; ++i ) {
            in[i] = 0, vis[i] = 0;
            dis[i] = inf;
        }
        //vis[u] = 1;
        dis[u] = 0;
        in[u] = 1;
        queue <int> q;
        q.push(u); 
        while(!q.empty()) {
            u = q.front();
            q.pop();
            vis[u] = 0;
            for (int i = head[u]; i ; i = nxt[i]) {
                int v = edge[i];
                int w = c[i];
                if(dis[v] > dis[u] + w) {
                    if(in[v] >= n + m) {
                        return true;
                    }
                    dis[v] = dis[u] + w;
                    if(!vis[v]) {
                        q.push(v);
                        vis[v] = 1;
                        ++in[v];
                    }
                }
            }
        }
        return false;
    }

    int t;

    int main()
    {
        read(t);
        while(t--) {
            int k;
            read(n); read(m); read(k);
            memset(head, 0, sizeof(head));
            cnt = 0;
            int s = n + m + 1;
            for ( int i = 1; i <= n + m; ++i ) {
                BuildGraph(s, i, 0);
            }
            for ( int i = 1; i <= k; ++i ) {
                int x, y, c;
                read(x); read(y); read(c);
                BuildGraph(x, y + n, c);
                BuildGraph(y + n, x, -c);
            }
            if(spfa(s)) {
                puts("No");
            }
            else {
                puts("Yes");
            }
        }
        return 0;
    }
  • 相关阅读:
    Java多线程简介
    Java同步简介
    java enum的用法详解
    Instrumentation（3）
    持久化类的三种实例状态
    依赖注入和控制反转
    事务的4个要素及其工作原理
    mysql创建表与索引
    SpringAOP所支持的AspectJ切点指示器
    使用Spring的命名空间p装配属性-摘自《Spring实战（第3版）》
  • 原文地址：https://www.cnblogs.com/orangeko/p/12894232.html
Copyright © 2011-2022 走看看