Floyd算法和Dijkstar算法是用来获得图中两点最短路径的算法。Dijkstar算法最终能够得到一个节点到其他所有节点的最短路径,而Floyd算法最终能够找出每对点之间的最短距离。
Dijkstar算法
问题描述:给定图G,求其顶点t到其他所有点的最短路径。
算法描述:将图所有点的集合S分为两部分,V和S-V。V集合是已经得到最短路径的点的集合,在初始情况下V中只有一个顶点t,S-V是还未得到最短路径点的集合。然后,在每一次迭代过程中取得S-V集中到V集合任一点距离最短的点,将其加到V集合,从V-S集合删除。重复此过程直到S-V集合为空。
时间复杂度: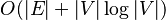
示例:


python实现:
 View Code
View Code
maxDis=1000000 def Dijkstar(G,t): n=len(G) # nodes number preNode=[t for i in range(0,n)] # the previous nodes distance=G[t][:] # the cur shortest distance short=[-1 for i in range(0,n)] #the final shortest diatance distance[t]=-1 short[t]=0 count=1 while count<n: minDis=maxDis minNode=-1 for i,dis in enumerate(distance): if dis>0 and dis<minDis: minNode=i minDis=dis count+=1 short[minNode]=minDis distance[minNode]=-1 # delete for j,disj in enumerate(distance): if disj<0: continue if minDis+G[minNode][j]< disj: distance[j]=minDis+G[minNode][j] preNode[j]=minNode return short,preNode if __name__=='__main__': G=[ [0,6,3,maxDis,maxDis,maxDis], [6,0,2,5,maxDis,maxDis], [3,2,0,3,4,maxDis], [maxDis,5,3,0,2,3], [maxDis,maxDis,4,2,0,5], [maxDis,maxDis,maxDis,3,5,0] ] short,prevNode=Dijkstar(G,0) print short
Floyd算法
问题描述:给定图G,得到每个点对的最短距离。
算法描述:Floyd算法是一个动态规划算法,最初矩阵A0是图的邻接矩阵,AK矩阵表示从i到j的最短路径,这些路径不能能通过大于K的节点,最终的矩阵AN就是想要得到的矩阵了。那么AK矩阵与A(K+1)矩阵有什么关系呢?关系就是A(K+1)[i,j]=min(A(K)[i,j],A(K)[i,k]+A(K)[k,j]),也就是看加上K点后,是不是能找到更短的距离。
时间复杂度:O(|V|^3) 顶点数的三次方。
示例:一上面的图为例子,下面展示了矩阵系列的建立过程:

python代码:
 View Code
View Code
import copy maxDis=1000000 def Floyd(G): n=len(G) path=copy.deepcopy(G) for k in range(0,n): for i in range(0,n): for j in range(0,n): path[i][j]=min(path[i][j],path[i][k]+path[k][j]) return path if __name__=='__main__': G=[ [0,6,3,maxDis,maxDis,maxDis], [6,0,2,5,maxDis,maxDis], [3,2,0,3,4,maxDis], [maxDis,5,3,0,2,3], [maxDis,maxDis,4,2,0,5], [maxDis,maxDis,maxDis,3,5,0] ] path=Floyd(G) for i in range(0,len(G)): print path[i]
