二叉树的遍历

这篇博客描述7种遍历二叉树的方式，其中三种是常用的前序、中序和后序遍历的递归算法，另外三种是前序、中序和后序遍历的非递归算法，最有一种是按层次的遍历。

（1）前序遍历，递归算法

public void preOrder(Node root){
        if(root==null){
            return;
        }
        visit(root);
        preOrder(root.left);
        preOrder(root.right);
    }

简单，不多说。

（2）中序遍历，递归算法

public void inOrder2(Node root){
        Stack<Node> S=new Stack<Node>();
        Node p=root;
        while(p!=null||!S.isEmpty()){
            while(p!=null){
                S.push(p);
                p=p.left;
            }
            p=S.pop();
            visit(p);
            p=p.right;
        }
    }

（3）后序遍历，递归算法

public void postOrder(Node root){
        if(root==null){
            return;
        }
        postOrder(root.left);
        postOrder(root.right);
        visit(root);
    }

（4）前序遍历，非递归算法

public void preOrder2(Node root){
        Stack<Node> S=new Stack<Node>();
        Node p=root;
        while(p!=null||!S.isEmpty()){
            while(p!=null){
                S.push(p);
                visit(p);
                p=p.left;
            }
            p=S.pop();
            p=p.right;
        }
}

这个算法用一个栈来保存节点的进出过程，节点进栈时访问节点。中序遍历的非递归算法和这个非常类似，只是在出栈的时候访问节点。

（5）中序遍历，非递归算法

public void inOrder2(Node root){
        Stack<Node> S=new Stack<Node>();
        Node p=root;
        while(p!=null||!S.isEmpty()){
            while(p!=null){
                S.push(p);
                p=p.left;
            }
            p=S.pop();
            visit(p);
            p=p.right;
        }
    }

（6）后序遍历，非递归算法

后序遍历的非递归算法有些麻烦。分析递归栈，你会发现到某个节点的时候无法确定它的右子树是否已经访问，如下图，从4回到2时应该把5压入栈，但是从5回到2应该输出2，但是如何区分这两种情况呢？面对这种困境，一般的想法就是多添加一个数据结构来记录某个节点的右子树是否已经被访问过了。

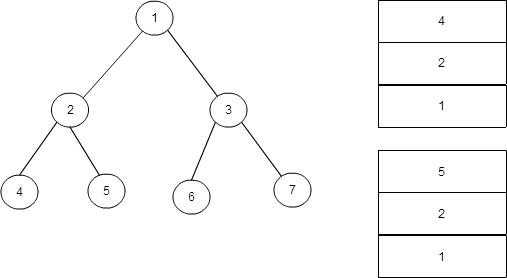
下面的算法用另外一个栈来记录某个节点的访问次数：初次访问时为1，此时压入左子树；再次访问时为2，此时表示右子树已经访问过，此时输出该节点。

void PostorderTraverse_nonRecursive(BinaryTreeNode* T)
{
    stack<BinaryTreeNode*> S;
    stack<int> S_count;
    BinaryTreeNode* p=T;
    while(!S.empty() || p)
    {
        while(p){
            S.push(p);
            S_count.push(1);
            p=p->left;
        }
        if(S_count.top()==2){
            cout << S.top()->value << ",";
            S.pop();
            S_count.pop();
        }
        else{
            int& count=S_count.top();
            count+=1;
            p=S.top()->right;
        }

    }

还有另外一种算法，参考http://blog.csdn.net/sgbfblog/article/details/7773103这篇文章，采用两个栈来记录节点情况。它根据这样一个观察：

后序遍历可以看作是下面遍历的逆过程：即先遍历某个结点，然后遍历其右孩子，然后遍历其左孩子。这个过程逆过来就是后序遍历。算法步骤如下：

1. Push根结点到第一个栈s中。
2. 从第一个栈s中Pop出一个结点，并将其Push到第二个栈output中。
3. 然后Push结点的左孩子和右孩子到第一个栈s中。
4. 重复过程2和3直到栈s为空。
5. 完成后，所有结点已经Push到栈output中，且按照后序遍历的顺序存放，直接全部Pop出来即是二叉树后序遍历结果。

public void postOrder2(Node root){
        Stack<Node> S1=new Stack<Node>();
        Stack<Node> S2=new Stack<Node>();
        
        S1.push(root);
        while(!S1.isEmpty()){
            Node p=S1.pop();
            if(p.left!=null) S1.push(p.left);
            if(p.right!=null)S1.push(p.right);
            S2.push(p);
        }
        while(!S2.isEmpty()){
            visit(S2.pop());
        }
    }

（7）层次遍历，按照层输出节点，一行一层

public void levelTravse(Node root){
        ArrayList<Node> queue=new ArrayList<Node>();
        int cur=0;    //current node
        int nextLevel=1;    //the start point of next level
        queue.add(root);
        while(cur<queue.size()){
            Node curNode=queue.get(cur);
            System.out.print(curNode.value+",");
            if(curNode.left!=null){
                queue.add(curNode.left);
            }
            if(curNode.right!=null){
                queue.add(curNode.right);
            }
            cur++;
            if(cur==nextLevel){
                nextLevel=queue.size();
                System.out.println();
            }
        }
    }

类似于图的层次遍历，但是这里没有用队列，用的是一个动态数组，这样能更好的记录层次信息。这种需要层次信息的，通常要用一个变量记录下一层开始的位置或者上一层结束的位置。