1. 问题
有2个一阶逻辑公式G(a, b, c), H(a, b, c),如何能够证明G == H,或者G != H
如:(A∧B) ∧ (A∨C) == B ∧ [A∨(A∧C)]
2. 常规解法
我们可以通过公式推导,将右边的公式转化为左边的
(A∧B) ∧ (A∨C)
= A∧B∧(A∨C)
= B ∧ [A∧(A∨C)]
= B ∧ [(A∧A)∨(A∧C)]
= B ∧ [A∨(A∧C)]
常规解法具有不确定性,带有尝试的味道在里面,需要人的经验和感觉,不适合计算机进行推导
3. 计算机的推导
可以遍历左右公式的真值表,如果真值表全相等,则他们是相等的
进一步,我们知道极小项就是公式真值表所有表达中的一项
如:
(A∧B∧C) == 1 的真值表解释为(1, 1, 1)
(A∧B∧~C)== 1 的真值表解释为(1, 1, 0)
而且书中已证明,2个公式的析取主范式相等,则2个公式相等,那么计算机可否自动求出任一一个公式的析取主范式呢?
我们来看看,析取主范式中的极小项和真值表的对应关系
上面的式子我们可以看出,公式为真时,只有唯一的一个极小项对应的真值表解释为True,所以是不是可以理解为一个公式的所有的极小项必须满足的条件:
公式在真值表中某一个解释为True时,其对应的极小项就是该析取主范式中的一项,如:
当A = 1, B = 1, C = 1时,I[(A∧B) ∧ (A∨C)] = 1
所以,可以说(A∧B∧C)就是该公式的一个极小项
G(a, b, c) = (X0_a ∧ X0_b ∧ X0_c) ∨ (X1_a ∧ X1_b ∧ X1_c) ∨ (X2_a ∧ X2_b ∧ X2_c) ∨ ... ∨ (Xn_a ∧ Xn_b ∧ Xn_c)... (Xn = X 或 ~X)
因为G(a, b, c)是用"∨"连接各个极小项的,所以要G(a, b, c) = 1,则必有一组极小项(Xn_a ∧ Xn_b ∧ Xn_c) = 1
那么当G(a, b, c) = 1,其他的(Xi_a ∧ Xi_b ∧ Xi_c) = 0的极小项是否也是该公式析取主范式的一项呢?
假设上述(Xi_a ∧ Xi_b ∧ Xi_c) = 0时,满足G(a, b, c) = 1,且(Xi_a ∧ Xi_b ∧ Xi_c)是G(a, b, c)析取主范式中的一个极小项
我们知道任何一个极小项在真值表中都有唯一的一个解释为True
∴ 当(Xi_a ∧ Xi_b ∧ Xi_c) = 1时,则G(a, b, c) = 0,否则就和假设相矛盾
∵ (Xi_a ∧ Xi_b ∧ Xi_c) 为析取主范式中的一项,且值为 1,因为析取主范式只要有一个极小项为1,则 G(a, b, c) = 1,与假设又相矛盾
∴ (Xi_a ∧ Xi_b ∧ Xi_c)必定不能为G(a, b, c)的极小项
∴ 求公式G(a, b, c)的析取主范式,只要遍历其真值表,然后写出G(a, b, c) = 1的真值表的极小项即可
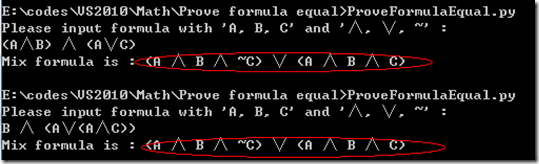
4. 算法实现(为了简单实现,不对公式进行语法解析,使用了python,且只求3个原子的公式的析取主范式,注意只能用“()”不能使用”[]”)
从计算机的自动推导结果可以看出,(A∧B) ∧ (A∨C) 和 B ∧ [A∨(A∧C)]的析取主范式是一样的,所以这2个公式相等,有兴趣的朋友可以去试试其他的公式证明
#!/usr/bin/env python #coding=utf8 import sys g_standardFormula = ""; g_formula = ""; def CheckFormulaValue(A, B, C): global g_formula; formulaResult = eval(g_formula); #formulaResult = (A and B) and (A or C); return formulaResult; def FormatMixFormula(trueArray): global g_standardFormula; beginChar = 65; #begin with A mixFormula = ""; for item in trueArray: if 1 == item: mixFormula += str(chr(beginChar)) + ' ∧ '; else: mixFormula += '~' + str(chr(beginChar)) + ' ∧ '; beginChar += 1; #去掉尾部多余的' ∧' #len()取特殊字符长度会将其长度计算为2,需要调整 maxSize = len(mixFormula) - len(' ∧ '); mixFormula = mixFormula[0:maxSize]; g_standardFormula += '(' + mixFormula + ') ∨ '; #trueArray = {A, B, C}每个位当前的值 def ProveFormula(index, trueArray): #{A, B, C}每个位各有(0, 1)2个值,每次遍历这2个值,然后递归遍历下一个位 #当index超过最后一个位时,判断是否和公式相等,如果相等则给出结果 if index >= len(trueArray): #当公式为'true'时,输出对应的极小项 if CheckFormulaValue(trueArray[0], trueArray[1], trueArray[2]): FormatMixFormula(trueArray); return; trueArray[index] = 0; ProveFormula(index + 1, trueArray); trueArray[index] = 1; ProveFormula(index + 1, trueArray); print u"Please input formula with 'A, B, C' and '∧, ∨, ~' : "; reload(sys); sys.setdefaultencoding('utf-8'); g_formula = raw_input(); g_formula = g_formula.decode('gbk'); g_formula = g_formula.replace('∧', ' and '); g_formula = g_formula.replace('∨', ' or '); g_formula = g_formula.replace('~', ' not '); initTrueArray = [0, 0, 0]; ProveFormula(0, initTrueArray); #去掉尾部多余的') ∨' g_standardFormula = g_standardFormula[0:len(g_standardFormula) - len(' ∨ ')]; print "Mix formula is :", g_standardFormula.decode('utf-8');