数据结构与算法（九）——查找

一、概述

1、介绍

　　静态查找：数据集合稳定，不会添加，删除元素的查找操作。
　　动态查找：数据集合在查找的过程中会添加，删除元素的查找操作。

2、查找方式

　　静态查找：不妨使用线性表结构组织数据，可以使用顺序查找算法；若对关键词排序，可以使用折半查找算法或斐波那契查找算法。
　　动态查找：可以使用二叉排序树的查找技术；还可以使用散列表结构来解决查找问题。
　　无序查找：顺序查找O(n)。
　　有序查找：折半查找O(log2n)、插值查找O(log2n)、斐波那契查找O(log2n)。三种有序表的查找本质上是分割点的选择不同，各有优劣，实际开发可根据数据的特点综合考虑再做决定。

3、平均查找长度（Average Search Length，ASL）

　　需和指定key进行比较的关键字的个数的期望值，成为查找算法在查找成功时的平均查找长度。
　　对于含有 n 个数据元素的查找表，查找成功的平均查找长度为：ASL = Pi*Ci的和。
　　Pi：查找表中第 i 个数据元素的概率。
　　Ci：找到第 i 个数据元素时已经比较过的次数。

二、顺序（线性）查找

1、思想

　　从第一个（或者最后一个）记录开始，逐个进行记录的关键字和给定值的比较，若某个记录的关键字和给定值相等，则查找成功。否则查找不成功。

2、代码

// 顺序查找.O(2n)
public static int orderSearch(int[] arr, int key) {
    for (int i = 0; i < arr.length; i++) {
        if (arr[i] == key) {
            return i;
        }
    }
    return -1;
}

三、折半（二分）查找

1、思想

　　取中间记录作为比较对象，若给定值与中间记录的关键字相等，则查找成功；若给定值小于中间记录的关键字，则在中间记录左半区继续查找；否则，在右半区查找。不断重复，直到查找成功或者查找失败为止。

2、代码

　　代码示例：返回单个

// 折半查找.O(log2n).方式一
public static int halfSearch(int[] arr, int key) {
    int left = 0, right = arr.length - 1, mid;

    while (left <= right) {
        mid = (left + right) / 2;

        if (key == arr[mid]) {
            return mid;
        }

        if (key < arr[mid]) {
            right = mid - 1;
        } else {
            left = mid + 1;
        }

    }
    return -1;
}

// 折半查找.方式二
public static int halfSearch2(int[] arr, int key) {
    int left = 0, right = arr.length - 1, mid;
    mid = (left + right) / 2;

    while (key != arr[mid]) {
        if (key < arr[mid]) {
            right = mid - 1;
        } else {
            left = mid + 1;
        }

        if (left > right) {
            return -1;
        }
        mid = (left + right) / 2;
    }
    return mid;
}

// 折半查找.方式三.递归
public static int halfSearch(int[] arr, int left, int right, int key) {
    if (left > right) {
        return -1;
    }

    int mid = (left + right) / 2;
    if (key == arr[mid]) {
        return mid;
    }

    if (key < arr[mid]) {
        return halfSearch(arr, left, mid - 1, key);
    } else {
        return halfSearch(arr, mid + 1, right, key);
    }
}

　　代码示例：返回多个

// 折半查找.返回多个 {1, 8, 10, 89, 1000, 1000, 1234}
public static List<Integer> halfSearch2(int[] arr, int left, int right, int key) {
    if (left > right) {
        return new ArrayList<>();
    }

    int mid = (left + right) / 2;
    if (key == arr[mid]) {
        List<Integer> result = new ArrayList<>();
        result.add(mid);

        // 向mid左边扫描
        int temp = mid - 1;
        while (temp >= 0 && arr[temp] == key) {
            result.add(temp);
            temp--;
        }

        // 向mid右边扫描
        temp = mid + 1;
        while (temp < arr.length && arr[temp] == key) {
            result.add(temp);
            temp++;
        }

        return result;
    }

    if (key < arr[mid]) {
        return halfSearch2(arr, left, mid - 1, key);
    } else {
        return halfSearch2(arr, mid + 1, right, key);
    }
}

四、插值（按比例）查找

1、思想

　　折半查找的改进算法，将折半查找的比例参数1/2改进了，根据关键字在整个有序表中所处的位置，让mid值的变化更靠近关键字key，这样也就间接地减少了比较次数。
　　适用于数据量较大，关键字分布较均匀。关键字分布不均匀时，该方法不一定比折半查找好。

2、代码

// 插值查找.
public static int insertSearch(int[] arr, int key) {
    int left = 0, right = arr.length - 1, mid;

    while (left <= right) {
        // 按比例改进mid
        mid = ((key - arr[left]) / (arr[right] - arr[left]) * (right - left)) + left;

        if (key == arr[mid]) {
            return mid;
        }

        if (key < arr[mid]) {
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    return -1;
}

// 插值查找.递归
public static int insertSearch(int[] arr, int left, int right, int key) {
    if (left > right || key < arr[0] || key > arr[arr.length - 1]) {
        return -1;
    }
    int mid = ((key - arr[left]) / (arr[right] - arr[left]) * (right - left)) + left;

    if (key == arr[mid]) {
        return mid;
    }

    if (key < arr[mid]) {
        return insertSearch(arr, left, mid - 1, key);
    } else {
        return insertSearch(arr, mid + 1, right, key);
    }
}

五、斐波那契查找（黄金分割法查找）

1、思想

　　折半查找的改进算法。优化 mid 的位置。

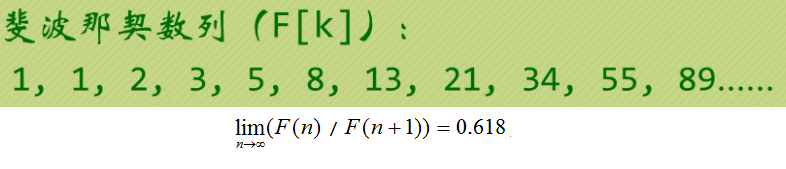
2、代码

 // Fibonacci查找
 public static int fibonacciSearch(int[] arr, int key) {
 
 
     return key;
 }

未完成。。。