我也不知道为啥要证明这玩意,但是我比较傻,看懂一遍之后怕忘了,所以还是写个博客。。
首先给出这么一个定义式:
$f(n)=sum_{dvert n}g(d)$
于是就有这么一个定理:
$g(n)=sum_{dvert n}mu(d)cdot f(frac nd)$
话说回来这个$mu(d)$就是莫比乌斯函数,定义是这样的
(1)若
(2)若

(3)其它情况下
于是有这样的性质
(1)对任意正整数
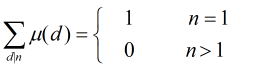
(2)对任意正整数
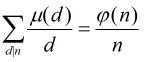
第一个性质其实还算好证。大概手玩一下组合数就行了。第二个我没推也没用上、、
下面是我xjb证的过程。。
首先要证$g(n)=sum_{dvert n}mu(d)cdot f(frac nd)$,只要证明右边等于$g(n)$。
右式$=sum_{dvert n}(mu(d)cdotsum_{evertfrac nd}g(e))$(定义式)
$=sum_{dvert n}sum_{evertfrac nd}(mu(d)cdot g(e))$(分配率)
稍微理解一下,发现其实是所有满足$(dcdot e)vert n$的二元组$(d,e)$之和。
于是可以交换前两个sum的位置即
$=sum_{evert n}sum_{dvertfrac ne}mu(d)cdot g(e)$
$=sum_{evert n}g(e)cdotsum_{dvertfrac ne}mu(d)$(分配率逆定律)
我们知道只有当$frac ne=1$即$e=1$的时候后半部分才等于1,其他情况都为0。所以就等于$g(n)$。
得证。
upd
发现以前的证明不够优美啊。狄利克雷卷积的证明真的让人愉悦~
详见知乎高票回答https://www.zhihu.com/question/23764267
话说回来,莫比乌斯反演的第二种形式
$g(n)=sum_{nvert d}mu(frac dn)f(d)$
求一个证明啊qwq


