序言
(CDQ) 分治和整体二分都是基于分治的思想,把复杂的问题拆分成许多可以简单求的解子问题。但是这两种算法必须离线处理,不能解决一些强制在线的题目。不过如果题目允许离线的话,这两种算法能把在线解法吊起来打(如树套树)。
前置知识:分治
个人觉得分治的经典例子便是归并排序。
大家都知道,归并排序就是每次将区间 ([l,r]) 拆分成 ([l,mid]) 和 ([mid+1,r]),然后再 (O(n)) 合并两个有序数组,再将 ([l,r]) 的答案传到上一层去。
那么我们可以得到 (T(n)=2 imes T(frac n2)+n)
因为这样递归层数不会超过 (log n) 层,所以时间复杂度为 (O(nlog n))
void mergesort(int l,int r){
if(l == r) return ;
int mid=(l+r)>>1;
mergesort(l,mid);
mergesort(mid+1,r);
int p=l,q=mid+1,cnt=l;
while(p<=mid&&q<=r){
if(a[p]<a[q]) t[cnt++]=a[p++];
else t[cnt++]=a[q++];
}
while(p<=mid) t[cnt++]=a[p++];
while(q<=r) t[cnt++]=a[q++];
for(int i=l;i<=r;i++) a[i]=t[i];
}
归并排序的另一个用途:求一个序列的逆序对。
我们发现在合并两个有序数组的时候,若 a[p]>a[q] 的时候,那么 (a[p]sim a[mid]) 的数一定比 (a[q]) 大,所以我们在归并排序的过程中加入一句 if(a[p]>a[q]) ans+=mid-l+1
这种思想在分治中非常有用。
(CDQ) 分治
讲 (CDQ) 分治的时候就少不了经典的多维偏序问题了。
二维偏序问题
给定 (n) 个元素,第 (i) 个元素有 (a_i)、(b_i) 两个属性,设 (f(i)) 表示满足 (a_jleq a_i) 且 (b_jleq b_i) 的 (j) 的数量。
对于 (din [0,n]),求满足 (f(i)=d) 的数量。
首先,我们可以把两个元素抽象成一个点 ((a,b)),那么我们就是求一个矩形中有多少个点。
比如我们要求这个矩形内有多少个点:
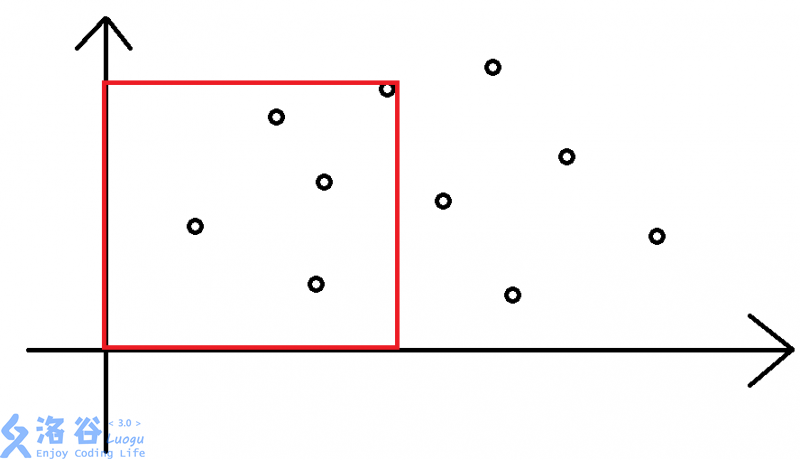
首先我们可以按照 (x) 轴排个序,发现矩形右边的点已经不在答案的贡献里了。那么 (f(i)) 就是在排序后的数组中找 (1sim i-1) 中有几个元素 (b) 比 (b_i) 小。
那么我们直接树状数组即可,时间复杂度 (O(nlog n))
#include <bits/stdc++.h>
#define lowbit(x) ((x)&(-(x)))
using namespace std;
const int maxn=100000+10;
int n,c[maxn],ans[maxn];
struct Stars{
int x,y;
}a[maxn];
bool cmp(Stars a,Stars b){
if(a.x!=b.x) return a.x<b.x;
return a.y<b.y;
}
inline int read(){
register int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return (f==1)?x:-x;
}
void add(int x,int y){
for(;x<maxn;x+=lowbit(x)) c[x]+=y;
}
int sum(int x){
int ans=0;
for(;x;x-=lowbit(x)) ans+=c[x];
return ans;
}
int main()
{
n=read();
for(int i=1;i<=n;i++)
a[i].x=read(),a[i].y=read();
sort(a+1,a+n+1,cmp);
int now;
for(int i=1;i<=n;i++){
now=sum(a[i].y+1);
ans[now]++;
add(a[i].y+1,1);
}
for(int i=0;i<n;i++)
printf("%d
",ans[i]);
return 0;
}
自己的题目:【模板】二维偏序
三维偏序问题
其实三维偏序就是在二维偏序上加一维而已。
我们先按每个元素的属性 (a) 排个序,然后第二维用归并排序,第三维用树状数组。
我们在归并的时候考虑 ([l,mid]) 对 ([mid+1,r]) 的贡献。因为我们已经按属性 (a) 排过序了,所以在排序属性 (b) 的时候,无论属性 (a) 怎么被打乱,([mid+1,r]) 所有元素的属性 (a) 一定不小于 ([l,mid]) 中所有元素的属性 (a),所以第二维是成立的。
在满足前两维都是有序的时候,类似二维偏序的解法,我们可以用树状数组来统计答案了。
在【模板】三维偏序中,(a_jleq a_i) 且 (b_jleq b_i) 且 (c_jleq c_i) 中是有取等号的,所以我们需要对元素进行去重,最后统计最终的答案,时间复杂度 (O(nlog^2 n))
例题:【模板】三维偏序
#include <bits/stdc++.h>
#define lowbit(x) ((x)&(-(x)))
using namespace std;
const int maxn=100000+10;
int n,m,c[maxn<<1],ans[maxn],cnt;
struct Element{
int a,b,c,w,f;
}e[maxn],t[maxn];
bool cmp(Element x,Element y){
if(x.a!=y.a) return x.a<y.a;
if(x.b!=y.b) return x.b<y.b;
return x.c<y.c;
}
inline int read(){
register int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return (f==1)?x:-x;
}
void update(int x,int y){
for(;x<=m;x+=lowbit(x)) c[x]+=y;
}
int sum(int x){
int ans=0;
for(;x;x-=lowbit(x)) ans+=c[x];
return ans;
}
void CDQ(int l,int r){
int mid=(l+r)>>1;
if(l==r) return ;
CDQ(l,mid);CDQ(mid+1,r);
int p=l,q=mid+1,tot=l;
while(p<=mid&&q<=r){
if(e[p].b<=e[q].b) update(e[p].c,e[p].w),t[tot++]=e[p++];
else e[q].f+=sum(e[q].c),t[tot++]=e[q++];
}
while(p<=mid) update(e[p].c,e[p].w),t[tot++]=e[p++];
while(q<=r) e[q].f+=sum(e[q].c),t[tot++]=e[q++];
for(int i=l;i<=mid;i++) update(e[i].c,-e[i].w);
for(int i=l;i<=r;i++) e[i]=t[i];
}
int main()
{
n=read();m=read();
for(int i=1;i<=n;i++)
e[i].a=read(),e[i].b=read(),e[i].c=read(),e[i].w=1;
sort(e+1,e+n+1,cmp);
cnt=1;
for(int i=2;i<=n;i++){
if(e[i].a==e[cnt].a&&e[i].b==e[cnt].b&&e[i].c==e[cnt].c) e[cnt].w++;
else e[++cnt]=e[i];
}
CDQ(1,cnt);
for(int i=1;i<=cnt;i++) ans[e[i].f+e[i].w-1]+=e[i].w;
for(int i=0;i<n;i++) printf("%d
",ans[i]);
return 0;
}
四维偏序问题
四维偏序就比较恶心了,需要 (CDQ) 套 (CDQ) 套 树状数组
怎么叫 (CDQ) 套 (CDQ) 呢?
我们可以在第二维 (CDQ) 的时候,记下那些元素在左区间还在右区间。在第三维 (CDQ) 的时候保持前两维的有序时,加一个树状数组,时间复杂度 (O(nlog^3 n))
不过这道题带修改,还要判断是什么操作。这里要保证时间的有序和 (x,y,z) 三维的有序,所以是四维偏序。
并且求在 ((x_1,y_1,z_1)) 和 ((x_2,y_2,z_2)) 的点对个数时要将这些限制拆成八个询问,容斥一下就好了。
#include <bits/stdc++.h>
#define lowbit(x) ((x)&(-(x)))
using namespace std;
const int maxn=400000+10;
int n,m,mp[maxn],c[maxn],ans[maxn],tot;
struct Element{
int op,x,y,z,w,id,flag;
}e[maxn],t[maxn],d[maxn];
inline int read(){
register int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return (f==1)?x:-x;
}
void add(int x,int y){
for(;x<maxn;x+=lowbit(x)) c[x]+=y;
}
int sum(int x){
int ans=0;
for(;x;x-=lowbit(x)) ans+=c[x];
return ans;
}
void CDQ3d(int l,int r){
if(l==r) return ;
int mid=(l+r)>>1;
CDQ3d(l,mid);CDQ3d(mid+1,r);
int p=l,q=mid+1,cnt=l;
while(p<=mid&&q<=r){
if(t[p].y<=t[q].y){
if(t[p].op==1&&t[p].flag==0)
add(t[p].z,1);
d[cnt++]=t[p++];
}
else {
if(t[q].op==2&&t[q].flag==1)
ans[t[q].id]+=t[q].w*sum(t[q].z);
d[cnt++]=t[q++];
}
}
while(p<=mid){
if(t[p].op==1&&t[p].flag==0)
add(t[p].z,1);
d[cnt++]=t[p++];
}
while(q<=r){
if(t[q].op==2&&t[q].flag==1)
ans[t[q].id]+=t[q].w*sum(t[q].z);
d[cnt++]=t[q++];
}
for(int i=l;i<=mid;i++){
if(t[i].op==1&&t[i].flag==0)
add(t[i].z,-1);
}
for(int i=l;i<=r;i++) t[i]=d[i];
}
void CDQ2d(int l,int r){
if(l==r) return ;
int mid=(l+r)>>1;
CDQ2d(l,mid);CDQ2d(mid+1,r);
int p=l,q=mid+1,cnt=l;
while(p<=mid&&q<=r){
if(e[p].x<=e[q].x){
t[cnt++]=e[p++];t[cnt-1].flag=0;
}
else {
t[cnt++]=e[q++];t[cnt-1].flag=1;
}
}
while(p<=mid){
t[cnt++]=e[p++];t[cnt-1].flag=0;
}
while(q<=r){
t[cnt++]=e[q++];t[cnt-1].flag=1;
}
for(int i=l;i<=r;i++) e[i]=t[i];
CDQ3d(l,r);
}
int main()
{
int T=read();
while(T--){
memset(ans,0,sizeof(ans));
m=read();tot=0;
int op,x1,y1,z1,x2,y2,z2,t=0;
for(int i=1;i<=m;i++){
op=read();
if(op==1){
x1=read(),y1=read(),z1=read();
e[++tot]=(Element){1,x1,y1,z1,1,tot,0};
}
else {
x1=read(),y1=read(),z1=read(),x2=read(),y2=read(),z2=read();
t++;
e[++tot]=(Element){2,x2,y2,z2,1,t,0};
e[++tot]=(Element){2,x1-1,y2,z2,-1,t,0};
e[++tot]=(Element){2,x2,y1-1,z2,-1,t,0};
e[++tot]=(Element){2,x2,y2,z1-1,-1,t,0};
e[++tot]=(Element){2,x1-1,y1-1,z2,1,t,0};
e[++tot]=(Element){2,x1-1,y2,z1-1,1,t,0};
e[++tot]=(Element){2,x2,y1-1,z1-1,1,t,0};
e[++tot]=(Element){2,x1-1,y1-1,z1-1,-1,t,0};
}
}
for(int i=1;i<=tot;i++) mp[i]=e[i].z;
sort(mp+1,mp+tot+1);
int cnt=unique(mp+1,mp+tot+1)-mp-1;
for(int i=1;i<=tot;i++) e[i].z=lower_bound(mp+1,mp+cnt+1,e[i].z)-mp;
CDQ2d(1,tot);
for(int i=1;i<=t;i++) printf("%d
",ans[i]);
}
return 0;
}
更高的偏序问题就要用到 (bitset) 啦,时间复杂度 (O(frac{n^2}{32})),今天就不讲了。
这道题离线做法就是化为 (Time_i<Time_j) 且 (Pos_i<Pos_j) 且 (Val_i<Val_j),然后用 (CDQ) 分治解决经典的三维偏序问题
整体二分
整体二分类似于一些决策单调性的分治,可以解决诸多区间第 (k) 小或区间第 (k) 大的问题。
整体二分 solve(l,r,L,R) 表示答案在 ([l,r]) 中,与操作 ([L,R]) 有关(操作 ([L,R]) 不一定对应原来 ([L,R]) 的操作)
我们就拿静态区间第 (k) 小来说好了。如果原序列的数 (leq mid),那么就在树状数组中对应位置 (+1)。如果碰到询问操作,那么查询询问区间 ([ql,qr]) 的值相当于查询了区间中值在 ([l,mid]) 的个数,如果个数 (leq k),那么答案在 ([mid+1,r]) 中,那么把 (k) 减掉对应的个数,把操作分到右区间。否则答案在 ([l,mid]) 中,把操作分到左区间。
如果 (l=r),那么直接把 (ans) 记录一下就好了。时间复杂度 (O(nlog^2 n))
不过我刚刚想到,如果将答案离散化一下,常数理论上会小下很多。读者有兴趣可以实现一下。
#include <bits/stdc++.h>
#define lowbit(x) ((x)&(-(x)))
using namespace std;
const int maxn=200000+10;
const int inf=1e9;
int n,m,a[maxn],c[maxn],ans[maxn],cnt;
struct Query{
int l,r,k,op,id;
}q[maxn<<1],q1[maxn<<1],q2[maxn<<1];
inline int read(){
register int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return (f==1)?x:-x;
}
void add(int x,int y){
for(;x<=n;x+=lowbit(x)) c[x]+=y;
}
int sum(int x){
int ans=0;
for(;x;x-=lowbit(x)) ans+=c[x];
return ans;
}
void solve(int l,int r,int L,int R){
if(L>R) return ;
if(l==r){
for(int i=L;i<=R;i++)
if(q[i].op==2) ans[q[i].id]=l;
return ;
}
int mid=(l+r)>>1,cnt1=0,cnt2=0,x;
for(int i=L;i<=R;i++){
if(q[i].op==1){
if(q[i].l<=mid) q1[++cnt1]=q[i],add(q[i].id,q[i].r);
else q2[++cnt2]=q[i];
}
else {
x=sum(q[i].r)-sum(q[i].l-1);
if(q[i].k<=x) q1[++cnt1]=q[i];
else q[i].k-=x,q2[++cnt2]=q[i];
}
}
for(int i=1;i<=cnt1;i++)
if(q1[i].op==1) add(q1[i].id,-q1[i].r);
for(int i=1;i<=cnt1;i++) q[L+i-1]=q1[i];
for(int i=1;i<=cnt2;i++) q[L+i+cnt1-1]=q2[i];
solve(l,mid,L,L+cnt1-1);
solve(mid+1,r,L+cnt1,R);
}
int main()
{
n=read(),m=read();
int l,r,k;
for(int i=1;i<=n;i++) a[i]=read(),q[++cnt]=(Query){a[i],1,0,1,i};
for(int i=1;i<=m;i++) l=read(),r=read(),k=read(),q[++cnt]=(Query){l,r,k,2,i};
solve(-inf,inf,1,cnt);
for(int i=1;i<=m;i++) printf("%d
",ans[i]);
return 0;
}
那么动态区间第 (k) 小带修改操作怎么搞呢?
我们可以把原来的减掉再加上后来的,然后跑一遍整体二分就好了。
#include <bits/stdc++.h>
#define lowbit(x) ((x)&(-(x)))
using namespace std;
const int maxn=200000+10;
const int inf=1e9;
int n,m,a[maxn],c[maxn],ans[maxn],cnt,tot;
struct Query{
int l,r,k,id,op;
}q[maxn*3],q1[maxn*3],q2[maxn*3];
inline int read(){
register int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return (f==1)?x:-x;
}
void add(int x,int y){
for(;x<=n;x+=lowbit(x)) c[x]+=y;
}
int sum(int x){
int ans=0;
for(;x;x-=lowbit(x)) ans+=c[x];
return ans;
}
void solve(int l,int r,int L,int R){
if(L > R) return ;
if(l == r){
for(int i=L;i<=R;i++)
if(q[i].op==2) ans[q[i].id]=l;
return ;
}
int mid=(l+r)>>1,cnt1=0,cnt2=0,x;
for(int i=L;i<=R;i++){
if(q[i].op==1){
if(q[i].l <= mid) q1[++cnt1]=q[i],add(q[i].id,q[i].r);
else q2[++cnt2]=q[i];
}
else {
x=sum(q[i].r)-sum(q[i].l-1);
if(q[i].k <= x) q1[++cnt1]=q[i];
else q[i].k-=x,q2[++cnt2]=q[i];
}
}
for(int i=1;i<=cnt1;i++)
if(q1[i].op==1) add(q1[i].id,-q1[i].r);
for(int i=1;i<=cnt1;i++) q[L+i-1]=q1[i];
for(int i=1;i<=cnt2;i++) q[L+i+cnt1-1]=q2[i];
solve(l,mid,L,L+cnt1-1);
solve(mid+1,r,L+cnt1,R);
}
int main()
{
n=read(),m=read();
int l,r,k;char op;
for(int i=1;i<=n;i++) a[i]=read(),q[++cnt]=(Query){a[i],1,0,i,1};
for(int i=1;i<=m;i++){
op=getchar();
while(!isalpha(op)) op=getchar();
if(op=='Q') l=read(),r=read(),k=read(),q[++cnt]=(Query){l,r,k,++tot,2};
else l=read(),r=read(),q[++cnt]=(Query){a[l],-1,0,l,1},q[++cnt]=(Query){a[l]=r,1,0,l,1};
}
solve(-inf,inf,1,cnt);
for(int i=1;i<=tot;i++) printf("%d
",ans[i]);
return 0;
}
我们把这个区间插入变成在线段树上区间增减,然后查询排名就相当于查询区间和。
不过线段树清空的时候直接再加一个懒标记在 (pushdown) 中下传就好了,不用像树状数组一样把原来加上的值减掉。