HDU 4832 Chess（DP+组合数学）（2014年百度之星程序设计大赛

Problem Description

　　小度和小良最近又迷上了下棋。棋盘一共有N行M列，我们可以把左上角的格子定为(1,1)，右下角的格子定为(N,M)。在他们的规则中，“王”在棋盘上的走法遵循十字路线。也就是说，如果“王”当前在(x,y)点，小度在下一步可以移动到(x+1, y), (x-1, y), (x, y+1), (x, y-1), (x+2, y), (x-2, y), (x, y+2), (x, y-2) 这八个点中的任意一个。


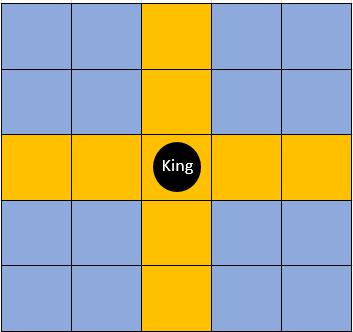
　　图1 黄色部分为棋子所控制的范围
　　小度觉得每次都是小良赢，没意思。为了难倒小良，他想出了这样一个问题：如果一开始“王”在(x₀,y₀)点，小良对“王”连续移动恰好K步，一共可以有多少种不同的移动方案？两种方案相同，当且仅当它们的K次移动全部都是一样的。也就是说，先向左再向右移动，和先向右再向左移动被认为是不同的方案。
　　小良被难倒了。你能写程序解决这个问题吗？

 

Input

输入包括多组数据。输入数据的第一行是一个整数T(T≤10)，表示测试数据的组数。
每组测试数据只包括一行，为五个整数N,M,K,x₀,y₀。(1≤N,M,K≤1000,1≤x₀≤N,1≤y₀≤M)

 

Output

对于第k组数据，第一行输出Case #k:，第二行输出所求的方案数。由于答案可能非常大，你只需要输出结果对9999991取模之后的值即可。

 

题目大意：略。

思路：很容易想到一个朴素的DP，dp[i][j][k]代表走k步走到坐标(i, j)的方案数，复杂度为O(nmk)，超时的节奏。

仔细想想，可以发现竖着走和横着走是独立的，于是分开考虑。

k步中，选i步横着走，那么有k-i步是竖着走的，设sumx[i]为横着走i步的方案数，sumy[k-i]为竖着走k-i步的方案数。

那么 ans = sum{c[k][i] * sumx[i] * sumy[k-i], 0 ≤ i ≤ k}，其中c[k][i]为组合数，意味在k步中选择i步横着走。

其中sumx[]可以用dp[i][j]表示走k步走到坐标i（一维）的方案数，复杂度为O(nk)，sum[y]同理。

于是总复杂度降到O(nk + mk)。

 

代码（750MS）;

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
typedef long long LL;

const int MOD = 9999991;
const int MAXN = 1010;

int f[] = {-2, -1, 1, 2};

int n, m, k, x0, y0, T;
int dpx[MAXN][MAXN], dpy[MAXN][MAXN];
int sumx[MAXN], sumy[MAXN];
int c[MAXN][MAXN];

void initc() {
    int n = 1000;
    c[0][0] = 1;
    for(int i = 1; i <= n; ++i) {
        c[i][0] = 1;
        for(int j = 1; j <= i; ++j)
            c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % MOD;
    }
}

bool check(int x, int n) {
    return 1 <= x && x <= n;
}

int solve() {
    memset(dpx, 0, sizeof(dpx));
    dpx[0][x0] = 1;
    for(int p = 1; p <= k; ++p) {
        for(int i = 1; i <= n; ++i) {
            for(int v = 0; v < 4; ++v) {
                int t = i + f[v];
                if(check(t, n)) dpx[p][t] = (dpx[p][t] + dpx[p - 1][i]) % MOD;
            }
        }
    }

    memset(sumx, 0, sizeof(sumx));
    for(int i = 0; i <= k; ++i) {
        for(int j = 1; j <= n; ++j) sumx[i] = (sumx[i] + dpx[i][j]) % MOD;
    }

    memset(dpy, 0, sizeof(dpy));
    dpy[0][y0] = 1;
    for(int p = 1; p <= k; ++p) {
        for(int i = 1; i <= m; ++i) {
            for(int v = 0; v < 4; ++v) {
                int t = i + f[v];
                if(check(t, m)) dpy[p][t] = (dpy[p][t] + dpy[p - 1][i]) % MOD;
            }
        }
    }

    memset(sumy, 0, sizeof(sumy));
    for(int i = 0; i <= k; ++i) {
        for(int j = 1; j <= m; ++j) sumy[i] = (sumy[i] + dpy[i][j]) % MOD;
    }

    LL ans = 0;
    for(int i = 0; i <= k; ++i)
        ans = (ans + LL(c[k][i]) * sumx[i] % MOD * sumy[k - i]) % MOD;

    return (int)ans;
}

int main() {
    initc();
    //cout<<c[1000][1000]<<endl;
    scanf("%d", &T);
    for(int t = 1; t <= T; ++t) {
        scanf("%d%d%d%d%d", &n, &m, &k, &x0, &y0);
        printf("Case #%d:
", t);
        printf("%d
", solve());
    }
}