分阶段求解问题。
最优子结构
状态转移公式
最优子结构
一、建模
有一座高度是10级台阶的楼梯,从下往上走,每跨一步只能向上1级或者2级台阶。要求用程序来求出一共有多少种走法。
比如,每次走1级台阶,一共走10步,这是其中一种走法。我们可以简写成 1,1,1,1,1,1,1,1,1,1。
再比如,每次走2级台阶,一共走5步,这是另一种走法。我们可以简写成 2,2,2,2,2。
当然,除此之外,还有很多很多种走法。
动态规划解决方法分析:
假设只差一步走到最后第10级台阶,会出现几种情况? ---------------> 最优子结构
两种:1、9级到10级,只剩一个阶梯
2、8级到10级,只剩两个阶梯
如果0到8级台阶的走法有X种,0到9级台阶的走法有Y种,则0到10级的台阶有X+Y种。
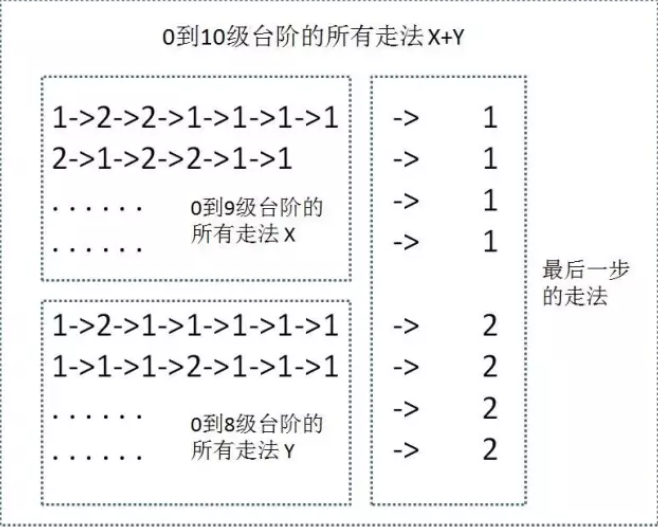
结论:
F(10) = F(8) + F(9)
同样:
F(9) = F(8) + F(7)
.............(正在把复杂问题分阶段进行简化,逐步简化成一个简单的问题,这就是动态规划)
当只有1级台阶或只有两级台阶的时候: ------------------> 边界
F(1) = 1
F(2) = 2
F(n) = F(n-1) + F(n-2) n>=3 ------------->状态转移公式
二、求解
方法一:递归

缺点:
要计算F(n),就要知道 F(n-1) 和 F(n-2)的值........
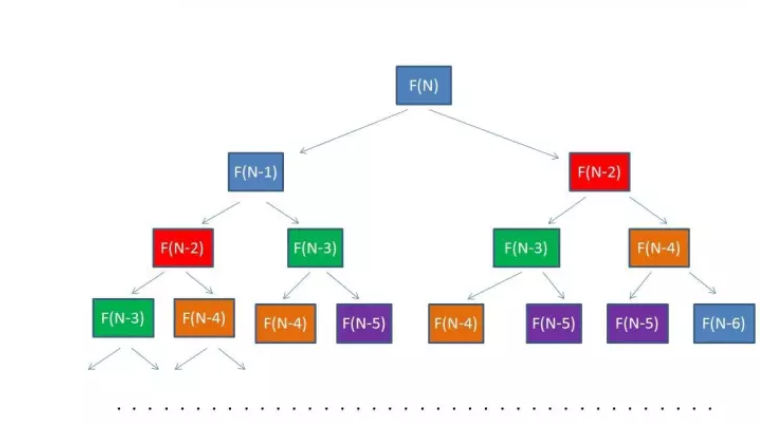
可以发现有很多重复计算了。
对于这些重复的计算的,可以用备忘录算法暂存一下。当每次需要计算F(N)的时候,会首先从map中寻找匹配元素。如果map中存在,就直接返回结果,如果map中不存在,就计算出结果,存入备忘录中。从F(1)到F(N)一共有N中不同的输入,在哈西表里存N-2个结果,时间复杂度和空间复杂度都是O(N)
方法二:自底向上,迭代推导出结果



可以发现,每次迭代过程中,只保留之前的的两个状态就行了,不需要像备忘录算法一样保留所有的子状态。

时间复杂度O(N),空间复杂度O(1)
题目二:国王和金矿
有一个国家发现了5座金矿,每座金矿的黄金储量不同,需要参与挖掘的工人数也不同。参与挖矿工人的总数是10人。每座金矿要么全挖,要么不挖,不能派出一半人挖取一半金矿。要求用程序求解出,要想得到尽可能多的黄金,应该选择挖取哪几座金矿?

一、最优子结构
如果第5个金矿选择挖,会占用掉一部人工人,前四个金矿工人=10 - 第5个金矿所需人数 = 10 -3 = 7;
如果第5个金矿不挖,那么就是10人4金矿时的最优选择。
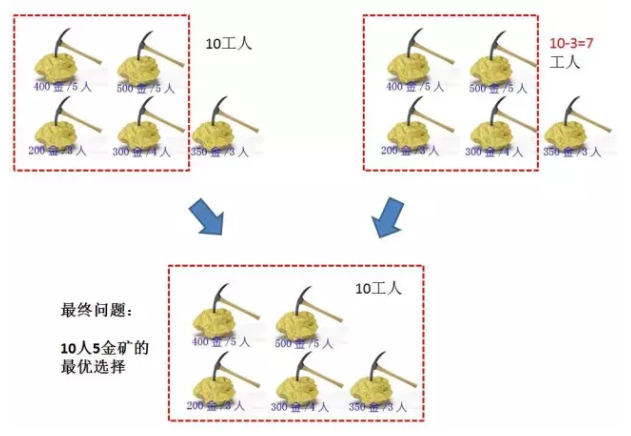
二、找到最优子结构,分析最优子结构和最终问题的关系
5个金矿的最优选择就是 (10人4金矿挖金的数量) 和 (前4金矿7人的挖金数量+第5金矿的挖金数量) 的最大值喽。
金矿数量 : N
工人总数: W
金矿黄金量设为数组:G[ ]
金矿用工人量数组:P[ ]
则:F[5,10] = MAX( F[4,10] ,F[ 4,10-P[4] ] )
三、边界
只有一座金矿。
如果给定的工人不够挖第一座金矿,W<P[0],得到的黄金量就是0;
如果给定的工人够挖第一座金矿,W>=P[0],得到的黄金量就是G[0]
四、综合得到状态转移方程
F(n,w) = 0 (n<=1, w<p[0]);
F(n,w) = g[0] (n==1, w>=p[0]);
F(n,w) = F(n-1,w) (n>1, w<p[n-1])
F(n,w) = max ( F(n-1,w) , F(n-1,w-p[n-1]) + g[n-1] ) (n>1, w>=p[n-1])
实现方法:
方法一、递归
时间复杂度是O(2^n)
方法二、备忘录算法
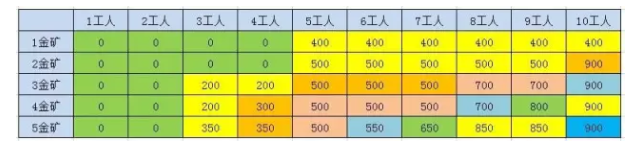
除了第一行,每个格子都是前一行的一个或者两个格子推到过来的。
所以使用程序实现的时候,也可以从左到右,从上到下一格一格推到出来。
所以并不需要存储整个表格,只需要存前一行的结果,就可以推导出新的一行。

方法利用两层迭代,来逐步推导出最终结果。在外层的每一次迭代,也就是对表格每一行的迭代过程中,都会保留上一行的结果数组 preResults,并循环计算当前行的结果数组results。
方法的时间复杂度是 O(n * w),空间复杂度是(w)。需要注意的是,当金矿只有5座的时候,动态规划的性能优势还没有体现出来。当金矿有10座,甚至更多的时候,动态规划就明显具备了优势。
注意:
把题目改变一下,如果总工人数变成1000,每个金矿的用工数量也增加,这个时候使用动态规划的时间复杂度是O(n*w = 5x1000=5000),开辟出1000个单位的空间;而简单递归时间复杂度是O(2^5=32),开辟5单位的空间。
此时动态规划的性能反而不如