正则化

对于同一个损失函数值，可以对应很多种不同的参数，甚至在高纬度下，极小值和极大值都很接近，所以即使是很好优化过的模型，也可能会对应多个不同的参数组合，很多组合都未必是数值稳定的。而且因为参数的安慰更自由，可以得到很小的训练误差，往往都不具有很好的泛化能力。

这个时候加入一个约束项，这个约束项计算之后，权重的绝对值就会整体的倾向于减小，特别是不会出现特别大的值。

为了解决过拟合问题。

解决过拟合的方法：

• 正则化
• 降维（特征选择，特诊图提取）
• 增加数据
• dropout

正则化是结构风险最小化策略的实现，在经验风险上加一个正则化项。作用是选择经验风险与模型复杂度同时较小的模型。

L2正则化（岭回归）

原来的目标函数如下图：

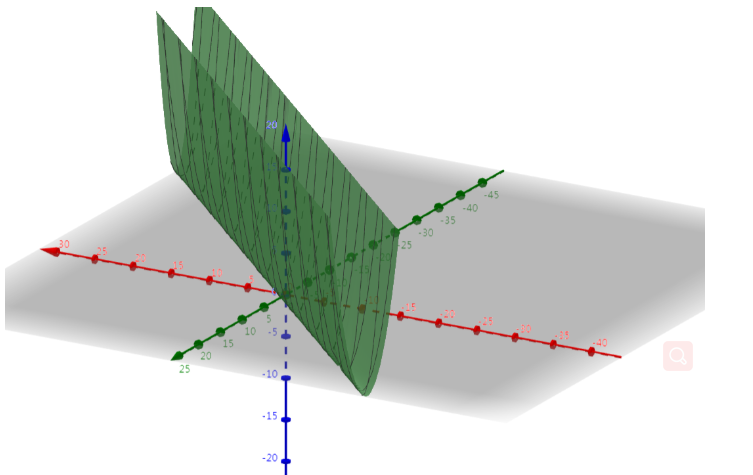
可以看出最小值是一条线，整个曲面是倒着的山岭，这样的曲面有无数个参数组合，单纯用梯度下降法很难得到确定解的。

正则项的图像如下图：

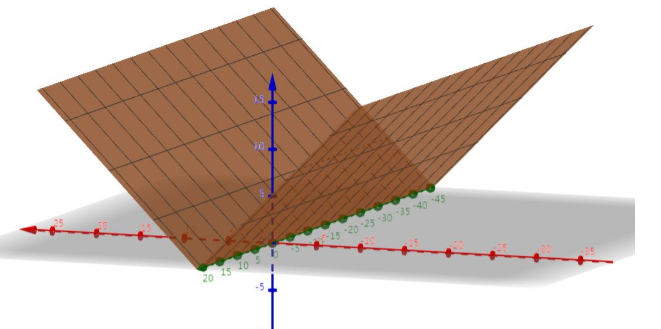
将正则项和目标函数叠加一起：

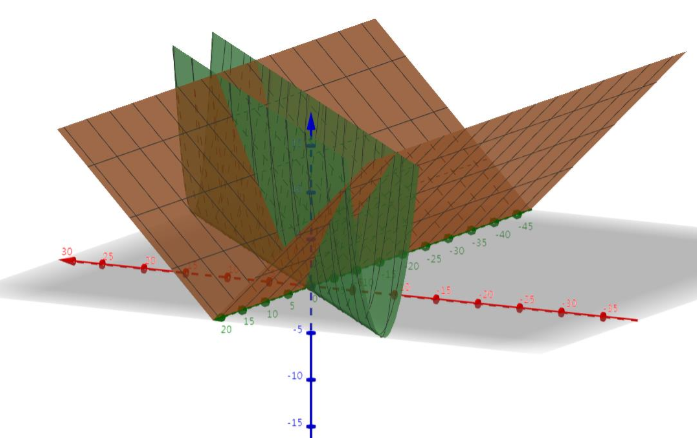
最后得到的最终图像：

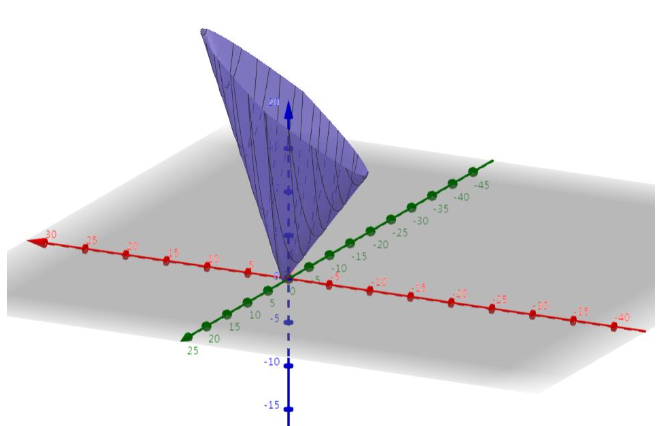
此时就像一个谷，这个时候就能使用梯度下降法来解决了。

这个例子还能看出，L2有帮助收敛的作用。

L1（Lasso）

和L2的区别主要是L2项的等高线不同。

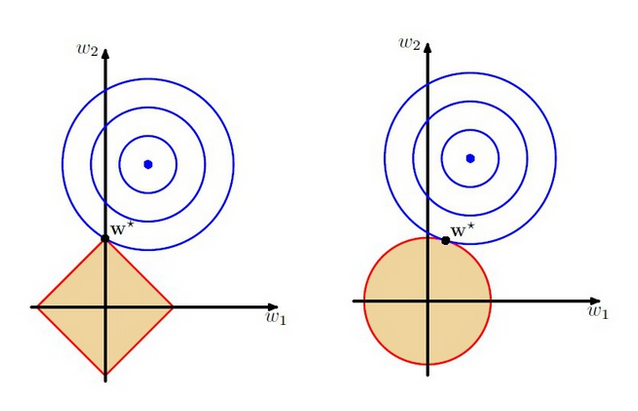
蓝色线：原目标函数等高线

红色线：正则项等高线

相交的地方为最优解

L2能让整体参数都有变小的趋势，而L1参数的方向是朝着某个轴靠近的，，且无论L1项的系数怎么变，最终最小值都一定是在横轴上的，这样的约束可以让有效特征的数量变小（在轴上，说明肯定有一大部分参数是0），获得稀疏性。

综上：

1. L1正则化可以产生一个稀疏权值矩阵，即产生一个稀疏模型，可用于特征选择。
2. L2可以防止模型过拟合，还使得优化求解变得稳定和迅速。
3. L2范数解决在用正规方程进行最小化代价函数是矩阵可能不可逆的问题。
   • 
4. Lasso在选择特征时非常有用，而Ridge就只是规则化而已。所以在所有特征中只有少数特征起重要作用的情况下，选择Lasso进行特征选择。而所有特征中大部分特征都能起作用，而且作用很平均，那么使用Ridge会更合适。