KD树算法是先对数据集进行建模,然后搜索最近邻,最后一步是预测。
KD树中的K指的是样本特征的维数。
一、KD树的建立
m个样本n维特征,计算n个特征的方差,取方差最大的第k维特征作为根节点。选择第k维特征的中位数作为切分点,小于中位数的放左子树,大于中位数的放右子树,递归生成。

举例
有二维样本6个,{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}:
1、找根节点,6个数据点在x、y维度上的方差分别是6.97,5.37,x维度方差最大,因此选择x维进行键树;
2、找切分点,x维中位数是(7,2),因此以这个点的x维度的取值进行划分;
3、x=7将空间分为左右两个部分,然后递归使用此方法,最后结果为:

(7,2)
/
(5,4) (9,6)
/ /
(2,3)(4,7) (8,1)
二、搜索最近邻
先找到包含目标点的叶子节点,然后以目标点为圆心,目标点到叶子节点距离为半径,得到超球体。最近邻的点一点在内部。
返回叶子节点的父节点,检查另一个叶子节点包含的超矩体是否和这个超球体相交,相交的话在这个叶子节点寻找有没有更近的近邻,更新。当回溯到根节点时,结束。此时保存的节点就是最近邻节点。
KD树划分后可以大大减少无效的最近邻搜索,很多样本点由于所在的超矩形体和超球体不相交,根本不需要计算距离。大大节省了计算时间。
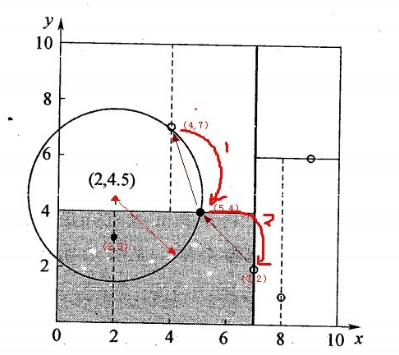
1、对(2,4.5)搜索最近邻,先从(7,2)开始找,2<7因此在左子树;
2、4.5>4,在右子空间找到叶子节点(4,7),计算距离为3.202,以它为半径得到超球体,返回父节点(5,4);
3、计算父节点与(2,4.5)的距离=3.041<3.202,更新保存的最近节点,同时由于左子空间与超球体相交,所以到左子空间中找有没有叶子节点;
4、左子空间中(2,3)节点与目标节点更近,找到最近邻。
三、KD树预测
在kd树搜索最近邻的基础上,选择到了第一个最近邻样本,把它设置为已选,然后第二轮中忽略这个样本,重新找最近邻。
四、球树
kd树对样本分布不均匀时,效果不好。
球树:每个分割快都是超球体。
过程:从球中选择一个离球的中心最远的点,然后选择第二个点离第一个点最远,将所有的点分配到这两个点上,计算聚类中心,然后对这两个小超球体递归使用这个方法